Выпуклые множества. Линейная комбинация выпуклых множеств. Замыкание и внутренность выпуклого множества. Выпуклая оболочка множества. Крайняя точка выпуклого множества, ее

Выпуклые множества. Линейная комбинация выпуклых множеств. Замыкание и внутренность выпуклого множества. Выпуклая оболочка множества. Крайняя точка выпуклого множества, ее

Экстремальное свойство выпуклой функции. О глобальности локального условного минимума выпуклой функции на выпуклом множестве. О выпуклости множеств точек минимума выпуклой функции. О единственности точки минимума строго выпуклой функции.

1. Теорема 1. Пусть f выпуклая функция на выпуклом множестве . Тогда всякая точка локального минимума функции f на множестве D является и точкой ее (глобального) минимума на множестве D.

Док-во. Так как x* - точка локального минимума функции f на множестве D, то существует такое, что , (1) где .

Предположим противное, то есть, что существует точка такая, что 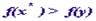. (2)

В силу выпуклости множества D, . Следовательно для достаточно малых 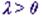. В силу (1), (2) и в силу выпуклости функции f на множестве D, для таких будем иметь .

Полученное противоречие доказывает теорему. Обозначим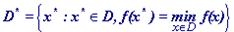

Теорема 2. Пусть f - строго выпуклая функция на выпуклом множестве . Тогда множество D* содержит не более чем одну точку.

Док-во. Пусть . Докажем, что оно состоит только из одной точки. Пусть это не так и существуют два вектора x* и y* принадлежащих множеству D*. Тогда, в силу выпуклости множества D* , и, в силу строгой выпуклости функции f, . Полученное противоречие доказывает теорему.

Теорема 4. Пусть f - выпуклая и дифференцируемая функция на выпуклом множестве . Тогда для того, чтобы точка была точкой минимума функции f на множестве D необходимо и достаточно, чтобы выполнялось неравенство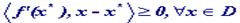

Док-во.Необ-сть. Пусть x* - точка минимума функции f на множестве D. Предположим 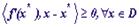(1) не имеет места. Тогда существует точка такая, что 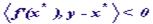. является направлением убывания функции f в точке x*. Следовательно, существует такое, что для любого , выполняется неравенство . (2) В силу вып-ти мн-ва D, . Тогда неравенство (2) при противоречит тому, что x* - точка минимума функции f на множестве D. Следовательно (1) имеет место.

Достаточность. Пусть в точке в точке имеет место (1). Отсюда и из (1) 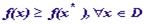. Что и требовалось.

8. Функция Лагранжа. Седловая точка функции Лагранжа. Условие дополняющей нежесткости. Теоремы о связи седловой точки функции Лагранжа с решением задачи нелинейного программирования. Основная идея: преобразование исходной задачи с ограничениями в задачу без ограничений. Для этого строится новая целевая функция – ф. Лагранжа, которая выражается через ф. целей исходной задачи, но число аргументов ф. Лагранжа увеличено на число ограничений данной задачи.

Пусть оптимизационная задача имеет след вид: найти min ф. z=f(x)->min (1) 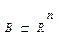- допустимая область определения системой ограничений

Это функция (n+m) переменных. (3) – ф. Лагранжа задачи 1-2 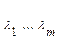- множество Лагранжа. Предполагается, что функции 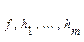являются непрерывно диф-мы к n>m; n-m – число степеней свободы задачи 1-2

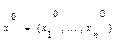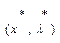Т. для того, чтобы вектор являлся решением оптимизационной задачи 1-2, необходимо, чтобы существовал такой вектор , что пара векторов удовлетворяла бы системе (n+m) алгебраических уравнений вида Пара векторов называют Седловой точкой функции Лагранжа , если вып соотношения и (4) для всех 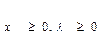Другими словами в Седловой точке достигается минимальное значение ф. Лагранжа по исходным переменным задачи математического программирования (по ч) и max знач по переменным

Т.1 (достаточное условие оптимальности) Если - седловая точка ф. Лагранжа задачи 1-2 в области неотрицательных значений аргументов ( 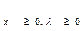), то вектор является оптимальным решением задачи 1-2 мат прог.

Док-во: Рассмотрим первое неравенство системы поскольку и неравенство вып для , то . Отсюда следует, что скалярное произведение 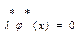, тогда правое неравенство системы (4) можно записать в виде поскольку для любого допустимого вектора x выполняется нер-во 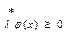, то в частности при будет выполняться условие , для всех

9. Задача выпуклого программирования. Построение допустимого множества задачи выпуклого программирования. Необходимое и достаточное условия существования оптимального решения задачи выпуклого программирования (Теорема Куна – Таккера). Определение 1 Задачей выпуклого программирования называется задача нелинейного программирования, у которой все функции являются выпуклыми функциями. Таким образом, задача выпуклого программирования является задачей минимизации выпуклой функции на выпуклом множестве, образованном системой выпуклых неравенств

Планом задачи ЛП называют всякий вектор

Допустимым планом ЗЛП называют такой план, который удовлетворяет системе ограничений.

Оптимальным планом ЗЛП называют допустимый план, при котором целевая функция достигает оптимального значения.

Допустимый план называется опорным планом ЗЛП, если векторы , входящие в разложение вектора с положительными коэффициентами ( ) являются линейно независимыми.

Опорный план называют невырожденным, если он содержит ровно m положительных компонент.

Решением задачи ЛП называется пара состоящие из оптимального плана и оптимального значения ЦФ

11. Основные свойства задачи линейного программирования. Эквивалентность базисных решений и крайних точек линейного многогранного множества. Основные понятия линейной алгебры и выпуклого анализа, применяемые в теории математического программирования. Кратко напомним некоторые фундамен­тальные определения и теоремы линейной алгебры и выпуклого анализа, которые широко применяются при решении проблем как линейного, так и нелинейного программирования.

Фундаментальным понятием линейной алгебры является линейное (вещественное) пространство. Под ним подразумевается множество некоторых элементов (именуемых векторами или точками), для которых заданы операции сложения и умножения на вещественное число (скаляр), причем элементы, являющиеся результатом выполнения операций, также в соответствии с определением должны принадлежать исходному про­странству.

Частными случаями линейных пространств являются вещественная прямая, плоскость, геометрическое трехмерное пространство.

Вектор λ ₁а + λ₂а*a + ...+ λ_та*a*...*a (a в степени m)называется линейной комбинацией векторов а', а².....

А в степ m с коэффициентами., λ_{1 …} λ_т

Система векторов линейного пространства а', а²,..., а в степ. m называется линейно зависимой, если существуют такие числа λ ₁… λ_т , не равные одновременно нулю, что их линейная комбинация λ ₁а + λ ₂a*a +... + λ _та^т равняется нулевому вектору (вектору, все компоненты которого равны нулю). В противном случае систему а¹, а²,..., а^т называют линейно независимой, т. е. линейная комбинация данных векторов может быть равна нулевому вектору только при нулевых коэффициентах лямбда.

Максимально возможное количество векторов, которые могут образовывать линейно независимую систему в данном линейном пространстве, называют размерностью простран­ства, а любую систему линейно независимых векторов в количестве, равном размерности, — базисом пространства.

Линейное пространство обычно обозначают как Rⁿ, где п — его размерность.

Любое подмножество данного линейного пространства, которое само обладает свойствами линейного пространства, называется линейным пространством. Множество H, получаемое сдвигом некоторого линейного подпространства 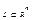на вектор а принадлежит Rⁿ: Н = L + а, называется аффинным множеством (пространством). Если фундаментальным свойством любого линейного пространства или подпространства является принадлежность ему нулевого вектора, то для аффинного множества это не всегда так. На плоскости примером подпространства является прямая, проходящая через начало координат, а аффинного множества — любая прямая на плоскости. Характеристическим свойством аффинного множества является принадлежность ему любой прямой, соединяющей две любые его точки.

Если рассматривается некоторое линейное пространство Rⁿ , то принадлежащие ему аффинные множества размерности 1 называются прямыми, а размерности (п— 1) — гиперплоскостями. Так, обычная плоскость является гиперплоскостью для трехмерного геометрического пространства К а прямая — гиперплоскостью для плоскости R². Всякая гиперплоскость делит линейное пространство на два полупространства.

Множество V векторов (точек) линейного пространства Rⁿназывается выпуклым, если оно содержит отрезок прямой, соединяющей две его любые точки, или, другими словами, из того, что а принадл. V и b принадл. V, следует, что x=(1-λ)*a + λb, где О < =λ <= 1.

Линейная комбинация векторов а¹, a²,..., а^mназывается выпуклой, если λ _i >= 0, i принадл. 1: т и

12. Эквивалентные формы постановки задачи линейного программирования, их особенности. Возможность приведения общей задачи линейного программирования к каноническому виду.

Линейное программирование – это раздел математики, в котором изучаются методы решения задач исследования операций связанных с эффективным использованием или распределением ограниченных ресурсов.

Эквивалентные формы постановки задачи ЛП:

1) Общая задача ЛП (ОЗЛП): Дана линейная целевая ф-ия и система ограничений , где - это один из знаков отношений ; 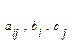- заданные действительные числа. - прямые ограничения

Требуется найти такие значения управляемых переменных, которые удовлетворяли бы системе ограничений(2),(3)и при этом определяют наибольшее или наименьшее значение целевой функции (1). ЗЛП называют разрешимой, если существует упорядоченный набор конечных значений удовлетворяющее всем ограничениям системы (2)(3) и обращающий целевую функцию (1) в max или min в зависимости от постановки задачи.

2)Математическая модель ЗЛП в стандартной форме: Максимизировать линейную целевую функцию, когда все ограничения являются неравенствами одного знака ( ) и на все управляемые переменные наложены условия неотрицательности.

; ;

Симметричная стандартная задача линейного программирования минимизировать линейную ЦФ 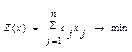, когда все ограничения являются неравенствами знака ( 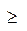) и на все управляемые переменные наложено условие неотрицательности.

3) Мат модель линейного программирования в канонической форме: Минимизировать линейную целевую функцию , когда все ограничения являются уравнениями и на все управляемые переменные наложено условие неотрицательности. . Введем обозначения: - матрица m на n, - вектор столбец свободных членов. - вектор столбец неизвестных. Стандартную ЗЛП можно записать ;

Выпуклые множества. Линейная комбинация выпуклых множеств. Замыкание и внутренность выпуклого множества. Выпуклая оболочка множества. Крайняя точка выпуклого множества, ее