
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Ранг матрицы, теорема о ранге матрицы
Системы линейных уравнений. Матрица и расширенная матрица
Определение 1. Матрицей порядка m´n называется таблица, состоящая из m строк и n столбцов. Если m = n, то матрица называется квадратной матрицей n-го порядка.
Матрица (2) называется матрицей системы (1). Матрица
 (3)
(3)
называется расширенной матрицей этой системы.
Отметим следующие свойства системы (1), часто помогающие при её решении.
· Если в системе (1) два или несколько уравнений поменять местами, то получится система уравнений, эквивалентная данной системе.
· Если в системе (1) одно из уравнений умножить на отличное от нуля действительное число, то получится система уравнений, эквивалентная данной.
· Если к одному из уравнений системы (1) прибавить другое её уравнение, умноженное на отличное от нуля действительное число, то получится система уравнений, эквивалентная данной.
· Если система (1) содержит два пропорциональных уравнения, то, удалив одно из этих уравнений, мы получим систему уравнений, эквивалентную данной.
· Если в системе (1) есть уравнение, все коэффициенты которого равны нулю, то после удаления этого уравнения мы получим систему уравнений, эквивалентную данной.
Описанные преобразования называются элементарными преобразованиями системы (1).
Соответствующие преобразования матрицы (3) называются элементарными преобразованиями этой матрицы.
Одним из методов решения системы (1) является метод последовательного исключения неизвестных или метод Гаусса.
Пусть дана система (1). Вместо того, чтобы преобразовывать эту систему, достаточно проводить соответствующие преобразования с её расширенной матрицей (3). Переставим, если нужно, строки матрицы так, чтобы в верхнем левом углу стоял отличный от нуля элемент. Будем считать, мто матрица (3) уже удовлетворяет этому условию. Умножив первую строку на число (-  ), прибавим её ко второй строке. В результате на первом месте во второй строке будет стоять 0. Умножив первую строку на число (-
), прибавим её ко второй строке. В результате на первом месте во второй строке будет стоять 0. Умножив первую строку на число (-  ), прибавим её к р-ой строке. В результате на первом месте в р-ой строке будет стоять 0. Сделаем это для всех р от 2 до m. Получим матрицу
), прибавим её к р-ой строке. В результате на первом месте в р-ой строке будет стоять 0. Сделаем это для всех р от 2 до m. Получим матрицу 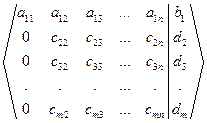 (4).
(4).
Если в матрице (4) есть строка, состоящая целиком из нулей, то её отбросим. Если есть пропорциональные строки, то из них оставим только одну. Пусть в матрице (4) все лишние строки уже отброшены. Строки с номерами 2, 3, … , m переставим, если нужно, так, чтобы во второй строке на втором месте стояло число, отличное от нуля. Пусть с22 ¹ 0. Умножим вторую строку на (-  ) и прибавим к к-ой строке для всех к от 3 до m. В результате все элементы второго столбца, кроме первых двух будут равны нулю. (Если в матрице (4) все ск2 равны нулю, то сразу переходим к третьей строке). Продолжая описанную процедуру дальше, мы получим либо треугольную, либо трапециевидную матрицу ( (5) или (6) ).
) и прибавим к к-ой строке для всех к от 3 до m. В результате все элементы второго столбца, кроме первых двух будут равны нулю. (Если в матрице (4) все ск2 равны нулю, то сразу переходим к третьей строке). Продолжая описанную процедуру дальше, мы получим либо треугольную, либо трапециевидную матрицу ( (5) или (6) ).
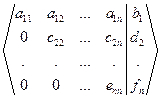 (5),
(5),  (6)
(6)
В этих матрицах все диагональные элементы, кроме может быть последнего, отличны от нуля.
Если матрица (3) привелась к виду (5), то система (1) эквивалентна системе
 (7)
(7)
Очевидно, еnn и fn не могут быть равны одновременно нулю. Если еnn ¹ 0, то система (7), а поэтому и система (1), имеет единственное решение. Действительно, из последнего уравнения можно найти хn. Подставив его значение в предпоследнее уравнение, найдём хn-1 и так далее. Если же еnn = 0, то fn ¹ 0. В этом случае последнее уравнение, а поэтому и вся система, не имеет решения.
Если матрица (3) привелась к виду (6), то система (1) будет эквивалентна системе
 (8)
(8)
Если  тогда
тогда  и последнее уравнение не имеет решений. Следовательно, не имеет решений и вся система. Если же коэффициенты
и последнее уравнение не имеет решений. Следовательно, не имеет решений и вся система. Если же коэффициенты  не все равны нулю, то последнее уравнение имеет бесконечно много решений (одно неизвестное этого уравнения можно выразить через остальные). Но тогда из предпоследнего уравнения можно найти
не все равны нулю, то последнее уравнение имеет бесконечно много решений (одно неизвестное этого уравнения можно выразить через остальные). Но тогда из предпоследнего уравнения можно найти  и, поднимаясь по системе, можно найти все неизвестные. Система будет иметь бесконечно много решений.
и, поднимаясь по системе, можно найти все неизвестные. Система будет иметь бесконечно много решений.
Теорема Кронекера-Капелли
). Система линейных уравнений совместна тогда и только тогда, когда ранг её матрицы равен рангу расширенной матрицы.
Доказательство. Þ Пусть система (25) совместна. Следовательно, существуют такие элементы a1, a2, … , an , что

Записав эти равенства в векторной форме, получим, что в = a1×а1+ a2×а2 + … + an×аn , где а1, а2, … , аn –векторы-столбцы матрицы А, в – вектор-столбец свободных членов. Из последнего равенства следует, что системы векторов а1, а2, … , аn и а1, а2, … , аn , в эквивалентны, поэтому их ранги равны. Итак, rang A = rang A1.
Ü Пусть rang A = rang A1 = к. Не нарушая общности, можно считать, что отличный от нуля минор к-го порядка в матрице А стоит в левом верхнем углу. Векторы-столбцы обозначим а1, а2, … , ак, ак+1, … , аn, в (*). Система а1, а2, … , ак будет максимальной линейно независимой подсистемой в системе (*), следовательно, найдутся такие коэффициенты х10, х20, … , хк0, что в = х10 а1+ х20 а2+ … + хк0 ак.Это равенство равносильно равенству в = х10 а1+ х20 а2+ … + хк0 ак+ … + 0×ак+1 + … + 0×аn. Перейдя к координатам, получим:
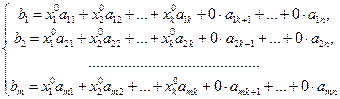 (28)
(28)
Отсюда следует, что (х10, х20, … , хк0, 0,… ,0) – решение системы (25), т.е. эта система совместна.
Из теоремы Кронекера – Капелли следуют правила решения системы линейных уравнений.
Для решения системы линейных уравнений достаточно
1. Найти ранги основной и расширенной матриц ( А и А1 ). Если rang A ¹ rang A1, то система не имеет решения.
2. Если rang A = rang A1 = к, то для решения достаточно оставить к уравнений, коэффициенты которых стоят на тех строчках матрицы А, на которых стоит базисный минор, и в этих уравнениях оставить в их левых частях те неизвестные, коэффициенты которых входят в базисный минор. Остальные неизвестные нужно перенести в правые части уравнений. Они могут принимать все возможные значения из поля Р. Эти неизвестные называются свободными. (Не нарушая общности, можно считать, что оставлены первые к уравнений и первые к неизвестных , система (29)).
 (29) (29)
| Определитель левой части системы (29) отличен от нуля, число уравнений равно числу неизвестных, поэтому (по теореме Крамера) эта система при всевозможных хк+1, … , хn имеет единственное решение. |
Следовательно, неизвестные х1, х2, … , хк можно выразить через хк+1, … , хn . Формулы, с помощью которых х1, х2, … , хк выражаются через хк+1, … , хn задают так называемое общее решение данной системы уравнений. При каждом конкретном наборе переменных хк+1, … , хn мы получим единственный набор х1, х2, … , хк . Это частное решение системы уравнений. Число свободных неизвестных равно n – к. Поэтому если к = n, то свободных неизвестных нет, система (29), а поэтому и система (25), имеет единственное решение. Если же к < n, то система имеет бесконечно много решений.
Пример. Исследовать систему уравнений и решить её, если она совместна в поле R.
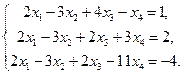
Решение. Составим матрицу и расширенную матрицу.
А1 = 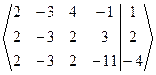
| Так как первый и второй столбцы пропорциональны, то для нахождения ранга матрицы один из них можно удалить. Будем считать, что удалён второй столбец. Минор М =  ¹ 0. ¹ 0.
|
Окаймим этот минор первым столбцом и третьей строкой , получим
D =  = 56 ¹ 0. = 56 ¹ 0.
| Следовательно, rang A = 3. Но rang A1 не может быть больше 3. Итак, rang A = rang A1 = 3. Для решения остаются три уравнения, т.е. все уравнения. Оставим в левых частях первое, третье и четвёртое неизвестные, второе неизвестное перенесём в правые части, |
получим

| Для этой системы D = 56,  = 84х2 , = 84х2 ,
|
 = 20,
= 20,  = 24. По формулам Крамера получаем х1 =
= 24. По формулам Крамера получаем х1 =  , х3 =
, х3 = 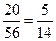 , х4 =
, х4 =  . Общее решение данной системы (
. Общее решение данной системы ( 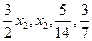 ), х2 – любое действительное число.
), х2 – любое действительное число.
Определение 43
| а) Р = R Будем говорить, что в действительном линейном пространстве L определено скалярное произведение векторов, если каждой упорядоченной паре векторов а и в из L поставлено в соответствие число (а, в) Î R, удовлетворяющее следующим требованиям (аксиомам скалярного произведения): 1. (а, в) = (в, а) для любых а и в из L; 2. (а + в, с) = (а, с) + ( в, с) для любых а, в, с из L; 3. (aа, в) = a(а, в) для любых а и в из L и любого a Î R; 4. (а, а) > 0, если а ¹ 0; (а, а) = 0 Û а = 0. | б) Р = С
Будем говорить, что в комплексном линейном пространстве L определено скалярное произведение векторов, если каждой упорядоченной паре векторов а и в из L поставлено в соответствие число (а, в) Î С, удовлетворяющее следующим требованиям (аксиомам скалярного произведения):
1.  = =  для любых а и для любых а и  из L;
2. (а + в, с) = (а, с) + ( в, с) для любых а, в, с из L;
3. (aа, в) = a(а, в) для любых а и в из L и любого a Î С;
4. (а, а) Î R и (а, а) > 0, если а ¹ 0; (а, а) = 0, если а = 0. из L;
2. (а + в, с) = (а, с) + ( в, с) для любых а, в, с из L;
3. (aа, в) = a(а, в) для любых а и в из L и любого a Î С;
4. (а, а) Î R и (а, а) > 0, если а ¹ 0; (а, а) = 0, если а = 0.
|
Скалярное произведение векторов можно обозначать (а, в) или а×в.
Определение 44. Действительное линейное пространство, в котором определено скалярное произведение векторов, называется евклидовым пространством.
Определение 45. Комплексное линейное пространство, в котором определено скалярное произведение векторов, называется унитарным пространством.
Так как и евклидово и унитарное пространства являются линейными пространствами, то для них верно всё то, что было сказано об этих пространствах. Но введение скалярного произведения позволяет ввести в этих пространствах метрику. В частности n-мерное линейное пространство, в котором введено скалярное произведение векторов, называется n-мерным евклидовым (или унитарным) пространством. Евклидово n-мерное пространство будем обозначать Еn (унитарное пространство - Un).
Примеры евклидовых пространств.
1. Пусть L – множество всех непрерывных на промежутке [a, b] действительных функций. Это множество является линейным пространством. Скалярное произведение определим по следующему правилу. Если f и g – две непрерывные на [a, b] функции, то пусть (f ,g) =  . Из свойств определённого интеграла следует, что все требования определения 43 (а) выполняются. Следовательно, если в пространстве всех непрерывных на промежутке [a, b] действительных функций ввести указанным способом скалярное произведение, то оно становится евклидовым пространством.
. Из свойств определённого интеграла следует, что все требования определения 43 (а) выполняются. Следовательно, если в пространстве всех непрерывных на промежутке [a, b] действительных функций ввести указанным способом скалярное произведение, то оно становится евклидовым пространством.
2. Пусть М2 – множество квадратных матриц с действительными элементами, это множество является линейным пространством на полем R. Определим скалярное произведение формулой  . Легко проверить, что все требования определения 43 (а) выполняются. Множество М2 стало евклидовым пространством.
. Легко проверить, что все требования определения 43 (а) выполняются. Множество М2 стало евклидовым пространством.
3. Пусть М2 – множество квадратных матриц с комплексными элементами, это множество является линейным пространством на полем С. Определим скалярное произведение формулой  . Легко проверит, что все требования определения 43 (б) выполняются. Получили пример унитарного пространства.
. Легко проверит, что все требования определения 43 (б) выполняются. Получили пример унитарного пространства.
Определение 46. Множество М элементов евклидова пространства Е называется подпространством пространства Е, если оно само является евклидовым пространством относительно того же скалярного произведения, что и Е. Аналогично определяется подпространство унитарного пространства.
Ранг матрицы, теорема о ранге матрицы
Пусть Р некоторое фиксированное поле и пусть А =  произвольная матрица размерности m ´ n. Каждый столбец матрицы можно рассматривать как m-мерныйвектор из m-мерного арифметического пространства Аm. Тогда система столбцов матрицы будет системой m-мерныхвекторов а1 = (а11, а21, … , аm1), а2 = (а12, а22, … , аm2), … , аn = (а1n, а2n, … , аmn).
произвольная матрица размерности m ´ n. Каждый столбец матрицы можно рассматривать как m-мерныйвектор из m-мерного арифметического пространства Аm. Тогда система столбцов матрицы будет системой m-мерныхвекторов а1 = (а11, а21, … , аm1), а2 = (а12, а22, … , аm2), … , аn = (а1n, а2n, … , аmn).
Определение 26. Столбцовым рангом матрицы А называется ранг системы её векторов – столбцов.
По аналогии со столбцами каждую строку матрицы А можно рассматривать как n-мерный вектор из n-мерного арифметического пространства Аn .
Определение 27. Строчным рангом матрицы А называется ранг системы её векторов – строк.
Теорема 18. Столбцовый ранг матрицы равен наибольшему порядку среди отличных от нуля её миноров.
Доказательство. Если все элементы матрицы – нули поля Р, то все её столбцы – нулевые вектора. Ранг этой системы векторов равен нулю. В матрице А все миноры первого порядка, все миноры второго порядка и т.д. равны нулю. Можно считать, что максимальный порядок отличных от нуля миноров равен нулю.
Пусть в матрице А не все элементы равны нулю, тогда в матрице есть отличные от нуля миноры. Выберем минор наибольшего порядка среди всех отличных от нуля. При перестановке столбцов ранг системы векторов-столбцов не изменится. При перестановке строк матрицы изменится только порядок координат векторов (при этом у всех векторов одинаково). Следовательно, эта перестановка тоже не изменит ранга системы векторов-столбцов. Переставим, если нужно, строки и столбцы матрицы так, чтобы выбранный нами минор М располагался в левом верхнем углу матрицы. Пусть его порядок равен к. Рассмотрим систему векторов-столбцов матрицы А. Обозначим их а1, … , ак, ак+1, … , аn . Векторы а1, … , ак линейно независимы, иначе выбранный нами минор был бы равен нулю. Покажем, что любой другой вектор-столбец через них линейно выражается. Для этого окаймим выбранный минор любым столбцом с номером к +1, к + 2, … , n и любой
а1, … , ак, ак+1, …, аn
А = 
| строкой. Если номер этой строки не больше к, то полученный определитель будет иметь две одинаковых строки, поэтому равен нулю. Если номер окаймляющей строки больше к, то это будет минор матрицы А порядка (к + 1), поэтому равен нулю по условию. Итак, определитель  равнее нулю при любом s, равном к + 1, … , n и любом р, равном 1, 2, … , m . равнее нулю при любом s, равном к + 1, … , n и любом р, равном 1, 2, … , m .
|
 = 0. = 0.
| Разложим  по последней строке, получим по последней строке, получим
 Так как М ¹ 0, то
Так как М ¹ 0, то  . .
|
Если номер столбца s зафиксирован, то алгебраические дополнения Ар1, … , Арк не меняются при изменении номера строки р. Следовательно, аs = 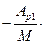 а1 – … –
а1 – … –  ак . Итак, любой вектор-столбец матрицы А линейно выражается через первые к её столбцов. Следовательно, столбцовый ранг матрицы равен к, т.е. наибольшему порядку отличных от нуля её миноров.
ак . Итак, любой вектор-столбец матрицы А линейно выражается через первые к её столбцов. Следовательно, столбцовый ранг матрицы равен к, т.е. наибольшему порядку отличных от нуля её миноров.
Следствие. Строчный ранг матрицы равен её столбцовому рангу.
Доказательство. Транспонируем матрицу А. При этом векторы-строки матрицы А станут векторами-столбцами транспонированной матрицы АТ. П ри транспонировании матрицы транспонируются и все её миноры. Так как при транспонировании определитель не меняется, то максимальный порядок отличных от нуля миноров в матрицах А и АТ один и тот же. По доказанной теореме столбцовые ранги этих матриц равны. Отсюда и следует утверждение следствия.
Так как столбцовый и строчный ранги матриц равны, то можно дать определение:
Определение 28. Рангом матрицы называется ранг системы её векторов-столбцов (или векторов-строк).
Из теоремы о ранге матрицы следует, что если мы найдём в матрице А минор М к-го порядка, отличный от нуля, то среди миноров (к + 1)-го порядка достаточно рассмотреть только те, которые получаются окаймлением минора М. Если они все равны нулю, то ранг матрицы равен к. В дальнейшем минор наибольшего порядка среди отличных от нуля будем называть базисным минором.
Пример. Найти ранг матрицы А =  в зависимости от b.
в зависимости от b.
Решение. Так как не все элементы матрицы равны нулю, то её ранг не меньше 1. Так как второй т третий столбцы одинаковы, то один из ни можно отбросить и находить ранг матрицы А1 =  . Из миноров второго порядка только один
. Из миноров второго порядка только один 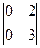 не содержит b, но этот минор равен 0. Рассмотрим минор М1 =
не содержит b, но этот минор равен 0. Рассмотрим минор М1 =  При b = 0 матрица А1 имеет вид
При b = 0 матрица А1 имеет вид  . В ней только один ненулевой столбец, следовательно, её ранг равен 1. Если
. В ней только один ненулевой столбец, следовательно, её ранг равен 1. Если 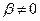 , то М1 ¹ 0, т.е. ранг матрицы не меньше 2. Минор М1 можно окаймить третьей строкой и третьим столбцом или четвёртой строкой и третьим столбцом. Получим М2 =
, то М1 ¹ 0, т.е. ранг матрицы не меньше 2. Минор М1 можно окаймить третьей строкой и третьим столбцом или четвёртой строкой и третьим столбцом. Получим М2 =  . Так как
. Так как 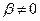 , то М2 ¹ 0. В матрице А1 миноров 4-го порядка нет, поэтому rang A = rang A1 = 3.
, то М2 ¹ 0. В матрице А1 миноров 4-го порядка нет, поэтому rang A = rang A1 = 3.
Итак, при b = 0 rang A = 1, при b ¹ 0 rang A =3.
Теорема 19. Элементарные преобразования матрицы не меняют её ранга.
Доказательство следует из того, что при элементарных преобразованиях матрицы мы получаем эквивалентные системы её векторов-строк.
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...