Под множеством будем понимать любую совокупность определенных и различимых между собой объектов, рассматриваемую как единое целое.

П.С. Довгий, В.И. Поляков,

В.И. Скорубский

Основы теории множеств

и приложение булевой алгебры

К синтезу комбинационных схем

Учебное пособие по дисциплине

«Дискретная математика»

Санкт-Петербург

Министерство образования и науки Российской Федерации

САНКТ-ПЕТЕРБУРГСКИЙ НАЦИОНАЛЬНЫЙ
ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ
ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЙ, МЕХАНИКИ И ОПТИКИ

П.С. Довгий, В.И. Поляков,

В.И. Скорубский

Основы теории множеств

и приложение булевой алгебры

К синтезу комбинационных схем

Учебное пособие по дисциплине

«Дискретная математика»

Санкт-Петербург

П.С. Довгий, В.И. Поляков, В.И. Скорубский. Основы теории множеств и приложение булевой алгебры к синтезу комбинационных схем. Учебное пособие по дисциплине «Дискретная математика». – СПб: НИУ ИТМО, 2012. – 109 с.

В пособии в краткой форме излагается материал по основным разделам дискретной математики, связанным со схемотехникой ЭВМ. К ним относятся теория множеств и булева алгебра.

Основное внимание уделяется не столько теоретическим вопросам, сколько техническим приложениям булевой алгебры к задачам анализа и синтеза комбинационных схем. В соответствии с этим достаточно детально рассмотрены методы решения задач минимизации, факторизации и декомпозиции булевых функций, а также преобразование минимальных и скобочных форм булевых функций к заданному функциональному базису. Аналогичные задачи и методы их решения рассмотрены также и применительно к системам булевых функций, что связано с построением многовыходных комбинационных схем.

В пособии приводится большое число практических примеров и задач, иллюстрирующих теоретический материал и облегчающих его восприятие. Каждый раздел пособия сопровождается контрольными вопросами и задачами для самостоятельной подготовки студентов к тестированию по каждой теме курса, а также к рубежному контролю по соответствующему модулю БАРС.

В 2009 году Университет стал победителем многоэтапного конкурса, в результате которого определены 12 ведущих университетов России, которым присвоена категория «Национальный исследовательский университет». Министерством образования и науки Российской Федерации была утверждена программа его развития на 2009–2018 годы. В 2011 году Университет получил наименование «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики».

Ó Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики, 2012

Ó П.С.Довгий, В.И. Поляков, В.И.Скорубский, 2012

Содержание

1. Основы теории множеств. 5

Введение……………………. 5

1.1. Основные понятия. 6

1.2. Способы задания множеств. 8

1.3. Отношения между множествами. 9

1.4. Алгебра множеств. 12

1.4.1 Операции над множествами. 12

1.4.2 Основные тождества (законы) алгебры множеств. 14

1.4.3 Способы доказательства тождеств. 16

1.5. Упорядоченные множества. 18

1.5.1 Понятие вектора. 18

1.5.2 Прямое (декартово) произведение множеств. 18

1.5.3 Декартова степень множества. 19

1.5.4 Мощность прямого произведения множеств. 20

1.5.5 Основные тождества для операции прямого произведения множеств.................... 20

Литература. ………………….………………………………………….20

Контрольные вопросы.. 21

Контрольные задачи. 22

2. Приложение булевой алгебры к синтезу комбинационных схем……24

Введение ………………………...............………………………………………….24

2.1. Элементы булевой алгебры.. 25

2.2. Разнообразие булевых функций. 28

2.3. Нормальные формы булевых функций. 30

2.4. Числовая и символическая формыпредставления булевых функций……………………………………………………………………..32

2.5. Преобразование произвольной аналитической формы булевой функции в нормальную.. 33

2.6. Приведение произвольных нормальных форм булевой функции к каноническим 34

2.7. Разнообразие двоичных алгебр. 34

2.8. Задача минимизации булевых функций. 35

2.8.1. Постановка задачи минимизации..............................................35

2.8.2. Методы минимизации булевых функций.................................36

2.9. Кубическое представление булевых функций. 41

2.10. Геометрическая интерпретация кубов малой размерности. Графическое представление булевых функций. 44

2.11. Покрытия булевых функций. 45

2.11.1. Построение покрытий булевых функций из кубов различной

размерности. Соответствие между покрытием и ДНФ булевой функции..................................................................................................45

2.11.2. Цена покрытия...........................................................................49

2.11.3. Нулевое покрытие булевой функции и получение МКНФ...51

2.12. Минимизация булевых функций на картах Карно. 52

2.12.1. Представление булевых функций на картах Карно...............52

2.12.2. Образование кубов различной размерности

на картах Карно.....................................................................................53

2.12.3. Определение минимальных покрытий и МДНФ...................55

2.12.4.Минимизация частично определенных булевых функций....57

2.13. Импликанты булевой функции. Системы импликант. 59

2.14. Минимизация булевых функций методом Квайна-Мак-Класки………….. 62

2.14.1 Нахождение множества максимальных кубов (простых импликант) булевой функци 62

2.14.2 Определение ядра покрытия. 64

2.14.3 Определение множества минимальных покрытий. 65

2.15. Функциональная полнота системы булевых функций. 69

2.15.1 Теорема о функциональной полноте (теорема Поста) 70

2.15.2 Замечательные классы булевых функций. 71

2.15.3 Конструктивный подход к доказательству функциональной полноты системы булевых функций. 73

Контрольные вопросы и задачи……………………………………...……74

3 Синтез комбинационных схем. 76

3.1. Типовые логические элементы и их обозначения на функциональных схемах 76

3.2. Способы кодирования логических сигналов. 77

3.3. Понятие логической схемы. Типы логических схем. 77

3.4. Основные параметры комбинационных схем. 79

3.5. Задачи анализа и синтеза комбинационных схем. 80

3.6. Построение комбинационных схем по минимальным нормальным формам в различных базисах. 83

3.6.1 Булев базис (И, ИЛИ, НЕ) 83

3.6.2 Сокращенный булев базис (И, НЕ). 84

3.6.3 Сокращенный булев базис (ИЛИ, НЕ) 85

3.6.4 Универсальный базис (И-НЕ) 85

3.6.5 Универсальный базис (ИЛИ-НЕ) 86

3.7. Задача факторизации булевой функции……….......…………...86

3.8. Оценка эффекта факторизации. 89

3.9. Декомпозиция булевых функций. 90

3.10. Синтез многовыходных комбинационных схем. 91

3.11. Минимизация системы булевых функций. 92

3.12. Факторизация системы булевых функций. 98

3.13. Декомпозиция системы булевых функций. 98

Контрольные вопросы и задачи ……………………………..…..………103

Вопросы к рубежному контролю……………...........………………….…..……105

Литература....................................................................................................107

Основы теории множеств

Введение

Вряд ли можно назвать какую-либо возникшую в последней трети девятнадцатого века математическую дисциплину, которая оказала бы большее влияние на прогресс всей математики и, шире, на математическое мышление в целом, чем теория множеств. К идеям теории множеств в разное время подходили с разных сторон многие ученые, но оформление ее в самостоятельную науку, со своими особыми предметом и методом исследования, осуществил в своих работах 1872-1897 г.г. немецкий математик Георг Кантор. Среди современников Г. Кантора правильно оценили значение этих работ только немногие, прежде всего Рихард Дедекинд, который внес собственный значительный вклад в новую теорию. Обнаруженные в конце ХIХ — начале ХХ вв. логические и методологические парадоксы теории множеств отпугнули некоторых выдающихся математиков, первоначально приветствовавших ее появление, в частности, таких как Анри Пуанкаре. Однако плодотворные приложения теории множеств в различных разделах математики стимулировали ее дальнейшую разработку во многих направлениях и исследование самых ее основ средствами бурно развивавшейся математической логики. Какие-либо окончательные и общепризнанные решения всех сложных проблем до сих пор не достигнуты и все более и более тонкие изыскания здесь продолжаются; вместе с тем современная математика не может обойтись без основного аппарата, понятий и приемов теории множеств.

Г. Кантору принадлежит заслуга привнесения в математику самого понятия "множества" (или "совокупности"). Это понятие относится к категории фундаментальных и неопределяемых понятий математики. Его можно толковать и иллюстрировать лишь на примерах. "Под множеством - писал Г. Кантор - я понимаю вообще всякое многое, мыслимое нами как единое, т.е. всякую совокупность определенных элементов, которая может быть связана в одно целое с помощью некоторого закона..." (Кантор Г. Труды по теории множеств. - М.: Наука, 1985. - С. 101) Г. Кантору принадлежит также следующая формулировка понятия множества: «Множество — это объединение определённых, различных объектов, называемых элементами множества, в единое целое».

Основные понятия

В основе теории множеств лежат первичные понятия: множествои отношение «быть элементоммножества».

Отношения между множествами

Два множества A и B могут вступать друг с другом в различные отношения.

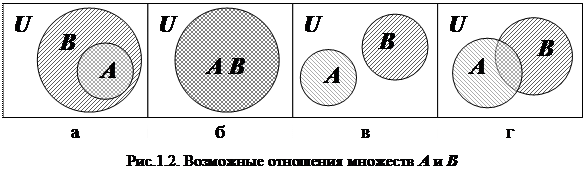
· Множество Aвключено в B, если каждый элемент множества A принадлежит также и множеству B (рис. 1.2 а), 1.2 б). Частным случаем отношения включения может быть и равенство множеств A и B, что отражается символом Í: AÍB Û "aÎA®a ÎB .

Подобное отношение можно называть нестрогим включением. Довольно часто требуется исключить равенство множеств из отношения включения, в связи с чем, вводится отношение строгого включения.

· Множество Aстрого включено в B, если A включено в B, но не равно ему (рис. 2а), что отражается символом Ì: AÌB Û (AÍB) и (A¹B).

Отношения между множествами могут обладать следующими свойствами: рефлексивностью, симметричностью и транзитивностью.

Свойство рефлексивности является унарным (одноместным), т.е. применительно к единственному объекту (в данном случае к множеству) и означает, что отношение применимо к «себе самому».

Простым примером рефлексивного отношения для чисел могут служить отношения «³» или «£», т.к. для любого числа d можно записать d ³ d или d £ d. В свою очередь отношения «>» и «<» этим свойством не обладают, в связи с чем, они называются антирефлексивными.

Свойство симметричности является бинарным (двухместным), т.е. применимо к двум объектам. Отношение является симметричным, если оно выполняется в обе стороны по отношению к паре объектов (в данном случае множеств). Примерами свойства симметричности являются различные геометрические объекты, для которых понятие «симметрии» является наиболее наглядным. Например, отношение: «быть симметричными относительно оси х» в отношении точек плоскости является симметричным. Действительно, если первая точка симметрична второй, то вторая точка обязательно симметрична первой.

В свою очередь, отношение между двумя объектами не обладает свойством симметричности, т.е. является антисимметричным, если его выполнение в обе стороны имеет место только в случае равенства объектов.

Если записать бинарное отношение между объектами a и b в общем виде aRb, где R – символ отношения, то для симметричного отношения: aRb ® bRa при любых a и b, а для антисимметричного aRb ® bRa, только, если a = b.

Примером антисимметричного отношения могут служить отношения «³» или «£» между числами. Действительно, (a £ b)®(b £ a), только, если a = b.

Свойство транзитивности являетсятернарным (трехместным), т.е. применяется к трем объектам. Отношение R между объектами a, b, с является транзитивным, если из aRb и bRс следует aRс, т.е. из выполнения отношения R между парами объектов (a, b) и (b, с) следует его выполнение и для пары (a, с). Примерами транзитивного отношения для чисел являются отношения «>», «³», «<», «£».

Отношение, не обладающее свойством транзитивности, называется нетранзитивным. Примером нетранзитивного отношения между множествами может служить отношение «пересекаться». Действительно для множеств: A={a, b},B={b, c}, C={c, d} A пересекается с B, B пересекается с C, но A не пересекается с C.

Отношение нестрогого включения обладает свойствами:

- рефлексивности: А ÍА;

- антисимметричности: (A Í В и B Í A) ® (A=B);

- транзитивности: (A Í В и B Ì C) ® (A Ì C).

Отношение строгого включения обладает свойствами:

- антирефлексивности: А Ë А;

A=B Û (AÍB) и (BÍA).

Вторая часть равенства указывает на наиболее типичный метод доказательства равенства множеств A и B, который заключается в доказательстве сначала утверждения АÍВ, а затем ВÍА.

Равные множества содержат одинаковые элементы, причем порядок элементов в множествах не существенен:

A={1, 2, 3} и В={3, 2, 1} ® A=B.

· множества A и Bне пересекаются, если у них нет общих элементов (рис. 1.2 в):

Aи B не пересекаются Û "aÎA® a ÏB.

A и B находятся в общем положении Û $a, b, c:[(aÎA) и (a ÏB)] и [(b ÎB) и (b ÏA)] и [(c ÎA) и (c ÎB)].

Рассмотрим отношения между числовыми множествами, для которых будем использовать следующие обозначения:

S– множество простых чисел;

N– множество натуральных чисел (т. е. N= {1, 2, 3, … });

Z– множество целых чисел;

Z+– множество целых неотрицательных чисел (иногда обозначается N₀ (т. е. N₀= {0, 1, 2, 3, … }));

Z–– множество целых неположительных чисел;

R– множество действительных чисел;

R+– множество неотрицательных действительных чисел;

R–– множество неположительных действительных чисел;

V– множество рациональных чисел;

W– множество иррациональных чисел;

К – множество комплексных чисел.

Для этих множеств очевидными являются следующие цепочки отношений включения:

· S Ì N Ì Z+Ì Z Ì V Ì R Ì К;

· W Ì R Ì К.

Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы одному из множеств А, В (рис. 1.3 а):

AÈB = {x | xÎ A или xÎB}.

Операцию объединения можно распространить на произвольное, в том числе и бесконечное количество множеств, например, М=АÈВÈСÈD. В общем случае используется обозначение А, которое читается так: “объединение всех множеств А, принадлежащих совокупности S ”.

Если же все множества совокупности индексированы (пронумерованы с помощью индексов), то используются другие варианты обозначений:

1. 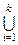А_i, если S={A₁,A₂,…,A_k};

2. А_i, если S – бесконечная совокупность пронумерованных множеств;

3. А_i, если набор индексов множеств задан множеством I.

Пример 1.2.

А={a,b,c}, B={b,c,d}, C={c,d,e}.

AÈB={a,b,c,d}; AÈC={a,b,c,d,e}; BÈC={b,c,d,e}; AÈBÈC={a,b,c,d,e}.

Пересечением множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат одновременно как множеству А, так и множеству В (рис. 1.3 б):

AÇB = {x | xÎ A и xÎB}.

Аналогично определяется пересечение произвольной (в том числе бесконечной) совокупности множеств. Обозначение для пересечения системы множеств аналогичны рассмотренным ранее обозначениям для объединения.

Пример 1.3. (для множеств из примера 1.2):

АÇВ={b,c}; AÇC={c}; BÇC={c,d}; AÇBÇC={c}.

Разностью множеств А и В называется множество всех тех и только тех элементов А, которые не содержатся в В (рис. 1.3 в):

A \ B = {x | xÎ A и xÏB}.

Разность множеств А и В иначе называется дополнением множества А до множества В (относительным дополнением).

Пример 1.4. (для множеств из примера 1.2)

А\В={а, b, c}\{b,c,d}={a}.

Симметрической разностью множеств А и В называется множество, состоящее из элементов, которые принадлежат либо только множеству А, либо только множеству В (рис. 1.3 г). Симметрическую разность обозначают как AΔB,A – B или A Å B:

AΔB ={x | (xÎ A и xÏB) или ( xÎ В и xÏА)}.

Таким образом, симметрическая разность множеств A и B представляет собой объединение разностей (относительных дополнений) этих множеств: AΔB = (A \ B) È (B \ A).

Пример 1.5. (для множеств из примера 1.2)

AΔB ={a}È{d}={a,d}.

Дополнением (абсолютным)множества А называется множество всех тех элементов хуниверсального множества U, которые не принадлежат множеству А (рис. 1.3 д). Дополнение множества Аобозначается :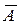

={x çxÏA}=U \ A.

Х – множество точек отрезка [0;1];

Y – множество точек отрезка [1;2].

Тогда Х´Y – множество точек квадрата с вершинами в точках (0,1), (0,2), (1,1), (1,2).

Декартова степень множества

Прямое (декартово) произведение одинаковых множеств называется декартовой степенью множества:

если В=А, то А´В=А´А=А².

Точка на плоскости может быть задана упорядоченной парой координат, т.е. двумя точками на координатных осях. Та как координаты представляются множеством действительных чисел R, то прямое произведение R´R=R² представляет собой множество координат точек плоскости.

Замечание. Метод координат ввел в употребление Рене Декарт, отсюда и название «декартово произведение».

Прямым (декартовым) произведением множеств А₁, А₂, …, А_n называется совокупность всех упорядоченных n-ок (векторов длиной n) (a₁, a₂, …, a_n) таких, что a_iÎAi (i=1,2,…,n). В случае, если А₁=А₂=…=А_n=А, то А₁´А₂´…´А_n = Аⁿ - n-ая декартова степень множества А.

Пример 1.12

Х – множество точек отрезка [0;1];

Y – множество точек отрезка [1;2];

Z – множество точек отрезка [0;0,5].

X´Y´Z – множество точек пространства, ограниченного параллелепипедом.

Замечание. Декартово произведение R´R´R= R³ представляет собой множество координат точек пространства.

Прямого произведения множеств

1. (АÇВ) ´ (CÇD) = (А´C) Ç (B´D);

2. (АÈВ) ´ C = (А´C) È(B´C);

3. (А\В) ´ C = (А´C) \(B´C);

4. А´(В\C) = (А´B) \(A´C).

Литература

1. Новиков Ф.А. Дискретная математика для программистов. 3-е изд. СПб.:Питер, 2009.–383 с.

2. Тюрин С.Ф. Дискретная математика: Практическая дискретная математика и математическая логика: учеб. пособие. /С.Ф.Тюрин, Ю.А. Аляев. – М.:Финансы и статистика, 2010. – 384 с.

3. Гладков Л.А., Курейчик В.В., Курейчик В.М.: Дискретная математика: теория множеств, алгоритмом, алгебры логики: Учебное пособие / Под ред. В.М.Курейчика. – Таганрог: изд-во ТТИ ЮФУ, 2009. – 312 с.

4. Нефедов В.Н., Осипова В.А. Курс дискретной информатики: Учеб. пособие. – М.:изд-во МАИ, 1992. – 264 с.

5. Кузнецов О.П. Адельсон-Вельский Г.М. Дискретная математика для инженеров. 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1988. – 480с.

Контрольные вопросы

Основные понятия, положения и формулировки

(В скобках приведены баллы за правильный и полный ответ)

1. Дать понятие:

- множества (3);

- подмножества (3);

- надмножества (3).

2. Какие способы используются для описания множеств? (2) Привести примеры различных способов описания и дать им пояснения. (5)

3. В чем состоит отличие между счетными и несчетными множествами? (2) Приведите примеры счетного и несчетного множества. (3)

4. Что понимается под мощностью множества? (2) Приведите пример множества А с мощностью |A|=8. (2)

5. Что понимается под абсолютным дополнением некоторого множества? (3)

6. Чему равна мощность булеана множества А, состоящего из шести элементов? (2)

7. Что понимается под взаимным включением множеств и в каком случае оно существует? (2)

8. В чем состоит отличие между строгим и нестрогим включением множеств? (3)

9. Что понимается под собственным подмножеством некоторого множества? (3)

10. Что понимается под свойством рефлексивности (симметричности, транзитивности) отношения? (3) Привести пример (примеры) отношений, обладающих этим свойством. (1 балл за каждый пример)

11. Что понимается под антирефлексивным (антисимметричным, нетранзитивным) отношением? (3) Привести пример (примеры) подобного отношения. (1 балл за каждый пример)

12. Является ли отношение параллельности двух прямых транзитивным? (1) Утверждение обосновать. (3)

13. Дать определение операции объединения (пересечения, разности, симметрической разности, дополнения) множеств. (3)

14. В каком случае объединение (пересечение, разность) двух множеств равно пустому (универсальному) множеству? (2)

15. Привести пример множеств, для которых пересечение равно Æ, а разность не равна Æ. (2)

16. Записать законы де Моргана (поглощения, склеивания, сокращения). (3)

17. Перечислите основные способы (методы) доказательства правомочности тождеств. (3) На чем основан тот или иной способ (метод) доказательства? (3)

18. Что понимается под прямым (декартовым) произведением трех множеств? (3) Чему равна мощность этого произведения? (2)

19. Для множества A={a, b} найти A³ – третью декартову степень. (3)

20. Записать основные тождества для операции прямого произведения множеств. (2 балла за каждое)

Контрольные задачи

1. Доказать тождества по определению равенства множеств (методом взаимного включения):

а) AÇ(BÈC)=(AÇB) È (AÇC) (5)

б) AÈ( ÇB)=AÈB (4)

в) AÇ(B−C)=(AÇB) − (AÇC) (10)

2. Доказать тождества с использованием других тождеств (алгебраическим способом):

а) AÇ( ÈB)=AÇB (2)

б) (АÈВ)Ç(АÈ )=А (2)

в) A \ (B \ C)=(A \ B)È(AÇC) (4)

3. С помощью диаграмм Эйлера-Венна (геометрическим способом) показать правомочность тождеств:

а) AÇ(BÈC)=(AÇB)È(AÇC) (3)

б) AÈ( ÇB)=AÈB (3)

в) (3)

г) A−(B−C)=(A−B)−C (5)

4. Убедится в правомочности тождества: A\(B\C)=(A\B)È(AÇC) на примере числовых множеств:

A={xÎN| x − нечётное и x £ 30},

B={xÎN| x делится на 3 и x £ 30},

C={xÎN| x делится на 5 и x £ 30}. (6)

5. Записать заданные множества перечислением их элементов:

а) A={xÎZ| x²+2x-3 < 0} (2)

б) B={xÎN₀| |x+1| £ 5} (3)

в) C={xÎZ| 0,1< 3^1-x < 100} (5)

г) D={xÎZ| −1< log₂|1−x| < 2} (5)

д) F={xÎR| sin²2x=1 и 0 £ x £ 2p} (4)

6. Изобразить на координатной плоскости следующие множества:

а) G={(x,y) ÎR²| |x − 1| − 1< y < 3 − |x+1|} (5)

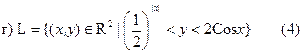
7. Действует ли коммутативный закон в отношении операции разности множеств? Утверждение обосновать. (3)

8. Проверить правомочность дистрибутивных законов для операций пересечения и разности (относительного дополнения) множеств с использованием диаграмм Эйлера-Венна (3 балла за каждый) и/или с использованием тождественных преобразований (5 баллов за каждый).

9. Убедиться в правомочности тождества A´(B \ C)=(A´B) \ (A´C) на примере заданных множеств: A:{a,b,c}, B={c,d,e}, C={a,b,d}. (5)

10. Упростить выражение: ((AÈB)ÇC)È( Ç( ÈC)) (4)

11. Доказать тождества:

а) (A \ B) − (B \ C) − (B \ A) − (C \ B)=A−C (4)

б) (A \B) È (B \ A)=(B \ A) − (A \ B) (4)

12. Записать множества, приведённые на диаграммах Эйлера-Венна: (3 балла за каждый)

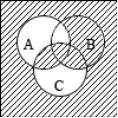
а) б) в)

2. Приложение булевой алгебры
к синтезу комбинационных схем

Введение

Теоретическим фундаментом современных ЭВМ является алгебра логики, основы которой разработал Дж. Буль. В 1847 году вышла его работа с характерным названием – “Математический анализ логики, являющийся опытом исчисления дедуктивного рассуждения”. Применяя алгебру (в дальнейшем она стала называться булевой алгеброй), можно было закодировать высказывания, истинность и ложность которых требовалось доказать, а потом оперировать ими, как в математике оперируют с числами. Дж. Буль ввел три основные операции: И, ИЛИ, НЕ, хотя алгебра допускает и другие операции – логические действия. Эти действия бинарны по своей сути, т.е. они оперируют с двумя состояниями: “истина” – “ложь”. Данное обстоятельство позволило в дальнейшем использовать булеву алгебру для описания переключательных схем. Добрых семьдесят лет после публикации его труд считался не более чем изящной, но чисто умозрительной конструкцией, пока Клод Шеннон не создал на основе булевой логики современную информатику. Клода Шеннона считают отцом теории информации и теории кодирования. Необходимо отметить, что окончательное оформление и завершение булева алгебра получила в работах последователей Дж. Буля: У.С. Джевонса и Дж. Венна (Англия), Э. Шредера (Германия), П.С. Порецкого (Россия).

Джордж Буль (англ. George Boole) (2.11.1815- 8.12.1864) английский логик, математик и философ

Клод Шеннон (англ. Claude Shannon) (30.04.1916 - 24.02.2001) американский инженер и математик

Элементы булевой алгебры

Основными элементами булевой алгебры являются:

· логические константы;

· переменные;

· операции;

· выражения;

· функции;

· законы.

Логические константы

В булевой алгебре определены две логические константы: логический ноль (0) и логическая единица (1), которые отождествляются с понятиями “истина” и ”ложь” алгебры логики.

Переменные

Булевы (логические, двоичные) переменные - переменные, принимающие значения из множества {0,1}.

Операции

Основными операциями булевой алгебры являются:

· отрицание (инверсия);

· конъюнкция (логическое умножение);

· дизъюнкция (логическое сложение).

Операция отрицания является унарной, а конъюнкция и дизъюнкция – n-арными.

Операции обозначаются следующим образом:

· Отрицание

· Конъюнкция a&b, a × b, a* b, ab, a Ù b;

· Дизъюнкция a Ú b.

Выражения

Логическим (<