Прямое (декартово) произведение множеств

Прямым (декартовым) произведением множествА и В называется множество всех пар (а,b), таких, что аÎА и bÎВ.

Прямое произведение множеств А и В обозначается в виде А´В:

А´В={(a,b)½aÎAиbÎB}.

Пример 1.10

А={a,b,c}; B={b,c}.

A´B={(a,b), (a,c), (b,b), (b,c), (c,b), (c,c)};

B´A={(b,a}, (b,b), (b,c), (c,a), (c,b), (c,c)}.

Замечание. Из рассмотренного примера видно, что А´В¹В´А, т.е. коммутативный закон для прямого произведения множеств не действует.

Пример 1.11

Х – множество точек отрезка [0;1];

Y – множество точек отрезка [1;2].

Тогда Х´Y – множество точек квадрата с вершинами в точках (0,1), (0,2), (1,1), (1,2).

Декартова степень множества

Прямое (декартово) произведение одинаковых множеств называется декартовой степенью множества:

если В=А, то А´В=А´А=А².

Точка на плоскости может быть задана упорядоченной парой координат, т.е. двумя точками на координатных осях. Та как координаты представляются множеством действительных чисел R, то прямое произведение R´R=R² представляет собой множество координат точек плоскости.

Замечание. Метод координат ввел в употребление Рене Декарт, отсюда и название «декартово произведение».

Прямым (декартовым) произведением множеств А₁, А₂, …, А_n называется совокупность всех упорядоченных n-ок (векторов длиной n) (a₁, a₂, …, a_n) таких, что a_iÎAi (i=1,2,…,n). В случае, если А₁=А₂=…=А_n=А, то А₁´А₂´…´А_n = Аⁿ - n-ая декартова степень множества А.

Пример 1.12

Х – множество точек отрезка [0;1];

Y – множество точек отрезка [1;2];

Z – множество точек отрезка [0;0,5].

X´Y´Z – множество точек пространства, ограниченного параллелепипедом.

Замечание. Декартово произведение R´R´R= R³ представляет собой множество координат точек пространства.

Мощность прямого произведения множеств

Теорема. Пусть А₁, А₂, …, А_n – конечные множества мощностью m₁, m₂, …, m_n. соответственно, т.е. ½А₁½=m₁,½A₂½=m₂, …,½A_n½=m_n.. Тогда мощность их прямого произведения равна произведению мощностей множеств – сомножителей, т.е.

½А₁´А₂´…´А_n½=m₁*m₂*…*m_n

Следствие: Мощность n-ой декартовой степенимножестваА равна n-ой степенимощности этого множества½Аⁿ½=½A½ⁿ

Основные тождества для операции

Прямого произведения множеств

1. (АÇВ) ´ (CÇD) = (А´C) Ç (B´D);

2. (АÈВ) ´ C = (А´C) È(B´C);

3. (А\В) ´ C = (А´C) \(B´C);

4. А´(В\C) = (А´B) \(A´C).

Литература

1. Новиков Ф.А. Дискретная математика для программистов. 3-е изд. СПб.:Питер, 2009.–383 с.

2. Тюрин С.Ф. Дискретная математика: Практическая дискретная математика и математическая логика: учеб. пособие. /С.Ф.Тюрин, Ю.А. Аляев. – М.:Финансы и статистика, 2010. – 384 с.

3. Гладков Л.А., Курейчик В.В., Курейчик В.М.: Дискретная математика: теория множеств, алгоритмом, алгебры логики: Учебное пособие / Под ред. В.М.Курейчика. – Таганрог: изд-во ТТИ ЮФУ, 2009. – 312 с.

4. Нефедов В.Н., Осипова В.А. Курс дискретной информатики: Учеб. пособие. – М.:изд-во МАИ, 1992. – 264 с.

5. Кузнецов О.П. Адельсон-Вельский Г.М. Дискретная математика для инженеров. 2-е изд., перераб. и доп. – М.: Энергоатомиздат, 1988. – 480с.

Контрольные вопросы

Основные понятия, положения и формулировки

(В скобках приведены баллы за правильный и полный ответ)

1. Дать понятие:

- множества (3);

- подмножества (3);

- надмножества (3).

2. Какие способы используются для описания множеств? (2) Привести примеры различных способов описания и дать им пояснения. (5)

3. В чем состоит отличие между счетными и несчетными множествами? (2) Приведите примеры счетного и несчетного множества. (3)

4. Что понимается под мощностью множества? (2) Приведите пример множества А с мощностью |A|=8. (2)

5. Что понимается под абсолютным дополнением некоторого множества? (3)

6. Чему равна мощность булеана множества А, состоящего из шести элементов? (2)

7. Что понимается под взаимным включением множеств и в каком случае оно существует? (2)

8. В чем состоит отличие между строгим и нестрогим включением множеств? (3)

9. Что понимается под собственным подмножеством некоторого множества? (3)

10. Что понимается под свойством рефлексивности (симметричности, транзитивности) отношения? (3) Привести пример (примеры) отношений, обладающих этим свойством. (1 балл за каждый пример)

11. Что понимается под антирефлексивным (антисимметричным, нетранзитивным) отношением? (3) Привести пример (примеры) подобного отношения. (1 балл за каждый пример)

12. Является ли отношение параллельности двух прямых транзитивным? (1) Утверждение обосновать. (3)

13. Дать определение операции объединения (пересечения, разности, симметрической разности, дополнения) множеств. (3)

14. В каком случае объединение (пересечение, разность) двух множеств равно пустому (универсальному) множеству? (2)

15. Привести пример множеств, для которых пересечение равно Æ, а разность не равна Æ. (2)

16. Записать законы де Моргана (поглощения, склеивания, сокращения). (3)

17. Перечислите основные способы (методы) доказательства правомочности тождеств. (3) На чем основан тот или иной способ (метод) доказательства? (3)

18. Что понимается под прямым (декартовым) произведением трех множеств? (3) Чему равна мощность этого произведения? (2)

19. Для множества A={a, b} найти A³ – третью декартову степень. (3)

20. Записать основные тождества для операции прямого произведения множеств. (2 балла за каждое)

Контрольные задачи

1. Доказать тождества по определению равенства множеств (методом взаимного включения):

а) AÇ(BÈC)=(AÇB) È (AÇC) (5)

б) AÈ( ÇB)=AÈB (4)

в) AÇ(B−C)=(AÇB) − (AÇC) (10)

2. Доказать тождества с использованием других тождеств (алгебраическим способом):

а) AÇ( ÈB)=AÇB (2)

б) (АÈВ)Ç(АÈ )=А (2)

в) A \ (B \ C)=(A \ B)È(AÇC) (4)

3. С помощью диаграмм Эйлера-Венна (геометрическим способом) показать правомочность тождеств:

а) AÇ(BÈC)=(AÇB)È(AÇC) (3)

б) AÈ( ÇB)=AÈB (3)

в) (3)

г) A−(B−C)=(A−B)−C (5)

4. Убедится в правомочности тождества: A\(B\C)=(A\B)È(AÇC) на примере числовых множеств:

A={xÎN| x − нечётное и x £ 30},

B={xÎN| x делится на 3 и x £ 30},

C={xÎN| x делится на 5 и x £ 30}. (6)

5. Записать заданные множества перечислением их элементов:

а) A={xÎZ| x²+2x-3 < 0} (2)

б) B={xÎN₀| |x+1| £ 5} (3)

в) C={xÎZ| 0,1< 3^1-x < 100} (5)

г) D={xÎZ| −1< log₂|1−x| < 2} (5)

д) F={xÎR| sin²2x=1 и 0 £ x £ 2p} (4)

6. Изобразить на координатной плоскости следующие множества:

а) G={(x,y) ÎR²| |x − 1| − 1< y < 3 − |x+1|} (5)

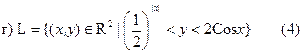
7. Действует ли коммутативный закон в отношении операции разности множеств? Утверждение обосновать. (3)

8. Проверить правомочность дистрибутивных законов для операций пересечения и разности (относительного дополнения) множеств с использованием диаграмм Эйлера-Венна (3 балла за каждый) и/или с использованием тождественных преобразований (5 баллов за каждый).

9. Убедиться в правомочности тождества A´(B \ C)=(A´B) \ (A´C) на примере заданных множеств: A:{a,b,c}, B={c,d,e}, C={a,b,d}. (5)

10. Упростить выражение: ((AÈB)ÇC)È( Ç( ÈC)) (4)

11. Доказать тождества:

а) (A \ B) − (B \ C) − (B \ A) − (C \ B)=A−C (4)

б) (A \B) È (B \ A)=(B \ A) − (A \ B) (4)

12. Записать множества, приведённые на диаграммах Эйлера-Венна: (3 балла за каждый)

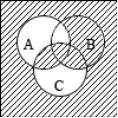
а) б) в)

2. Приложение булевой алгебры
к синтезу комбинационных схем

Введение

Теоретическим фундаментом современных ЭВМ является алгебра логики, основы которой разработал Дж. Буль. В 1847 году вышла его работа с характерным названием – “Математический анализ логики, являющийся опытом исчисления дедуктивного рассуждения”. Применяя алгебру (в дальнейшем она стала называться булевой алгеброй), можно было закодировать высказывания, истинность и ложность которых требовалось доказать, а потом оперировать ими, как в математике оперируют с числами. Дж. Буль ввел три основные операции: И, ИЛИ, НЕ, хотя алгебра допускает и другие операции – логические действия. Эти действия бинарны по своей сути, т.е. они оперируют с двумя состояниями: “истина” – “ложь”. Данное обстоятельство позволило в дальнейшем использовать булеву алгебру для описания переключательных схем. Добрых семьдесят лет после публикации его труд считался не более чем изящной, но чисто умозрительной конструкцией, пока Клод Шеннон не создал на основе булевой логики современную информатику. Клода Шеннона считают отцом теории информации и теории кодирования. Необходимо отметить, что окончательное оформление и завершение булева алгебра получила в работах последователей Дж. Буля: У.С. Джевонса и Дж. Венна (Англия), Э. Шредера (Германия), П.С. Порецкого (Россия).

Джордж Буль (англ. George Boole) (2.11.1815- 8.12.1864) английский логик, математик и философ

Клод Шеннон (англ. Claude Shannon) (30.04.1916 - 24.02.2001) американский инженер и математик

Элементы булевой алгебры

Основными элементами булевой алгебры являются:

· логические константы;

· переменные;

· операции;

· выражения;

· функции;

· законы.

Логические константы

В булевой алгебре определены две логические константы: логический ноль (0) и логическая единица (1), которые отождествляются с понятиями “истина” и ”ложь” алгебры логики.

Переменные

Булевы (логические, двоичные) переменные - переменные, принимающие значения из множества {0,1}.

Операции

Основными операциями булевой алгебры являются:

· отрицание (инверсия);

· конъюнкция (логическое умножение);

· дизъюнкция (логическое сложение).

Операция отрицания является унарной, а конъюнкция и дизъюнкция – n-арными.

Операции обозначаются следующим образом:

· Отрицание

· Конъюнкция a&b, a × b, a* b, ab, a Ù b;

· Дизъюнкция a Ú b.

Выражения

Логическим (булевым) выражением называется совокупность булевых переменных, соединенных знаками булевых операций при возможном наличии скобок для изменения порядка выполнения операций.

При отсутствии скобок порядок выполнения операций определяется их приоритетом (значимостью). Для булевых операций порядок убывания приоритета следующий: ù , &, Ú.

Примеры логических выражений: .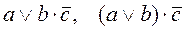

Функции

Булевой (логической) функцией называется функция, аргументами которой являются булевы переменные, а сама функция принимает значение из множества {0,1}.

Областью определения булевой функции является совокупность 2ⁿ двоичных наборов ее аргументов. Набор аргументов можно рассматривать как n-компонентный двоичный вектор.

Булеву функцию можно задать с помощью следующих форм:

· аналитической;

· табличной;

· графической;

· таблично-графической;

· числовой;

· символической.

Аналитическая форма – булева функция задается логическим выражением, например:

Табличная форма – булева функция задается таблицей истинности.

Переход от аналитической формы к табличной однозначен. Обратный переход однозначным не является.

В качестве примера составим таблицу истинности для функции y₁:

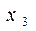
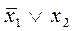
				y

Остальные формы задания булевой функции рассматриваются в следующих разделах.