Кубическим представлением булевой функции

Любому кубу из К(f) можно поставить в соответствие конъюнктивный терм, который можно рассматривать как импликанту булевой функции. Любой простой импликанте булевой функции соответствует максимальный куб, и, в свою очередь, множество всех простых импликант соответствует множеству Z(f) всех максимальных кубов К(f). Таким образом, можно провести некоторую аналогию между сокращенной СДНФ и Z(f).

В отношении импликант булевой функции также как и в отношении кубов, соответствующих им, существует отношение покрытия.

Принято считать, что импликанта булевой функции покрывает некоторую существенную вершину этой функции или, в общем случае, некоторый куб из К(f), если значение импликанты на наборе аргументов, представляющем данную существенную вершину, равно 1 или, в общем случае, значение импликанты равно 1 для всех существенных вершин покрываемых кубом из К(f).

Наример, импликанта х₁х₂ покрывает существенные вершины (110, 111) и в свою очередь покрывает куб 11Х.

Множество импликант булевой функции образует полную систему импликант, если любая существенная вершина булевой функции покрывается хотя бы одной импликантой этого множества.

Если считать, что в полную систему импликант включаются импликанты только в виде конъюнктивных термов и не включаются импликанты в виде дизъюнкции термов, то полной системе импликант можно поставить в соответствие некоторое множество кубов из К(f) образующих покрытие булевой функции f .

Так, например, кубам из кубического комплекса К° (f) соответствует полная система импликант, представляющая собой множество конституент 1 данной функции f. В свою очередь, множеству максимальных кубов Z(f), естественно образующих покрытие булевой функции, соответствует полная система простых импликант.

Система простых импликант называется приведенной, если она является полной, а никакая ее собственная часть уже не образует полную систему импликант.

Пример 2.17. Проверить, является ли система простых импликант 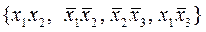для функции полной и, если да, то является ли она приведенной.

Для функции 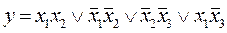система простых импликант 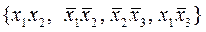является полной, но не является приведенной, т.к. из нее можно исключить одну из импликант не нарушая полноты системы.

Дизъюнкция всех простых импликант, образующих некоторую приведенную систему называется тупиковой ДНФ булевой функции или ТДНФ.

Минимизация булевых функций методом

Квайна-Мак-Класки

Для решения канонической задачи минимизации методом Квайна-Мак-Класки применяется следующая последовательность действий:

1. Нахождение множества максимальных кубов (простых импликант) булевой функции.

2. Выделение ядра покрытия (определение множества существенных импликант).

3. Дополнение множества кубов, принадлежащих ядру покрытия, минимальным подмножеством из множества максимальных кубов, не входящих в ядро покрытия, для получения покрытия с минимальной ценой.

С точки зрения последовательного преобразования ДНФ булевой функции с целью их упрощения каноническая задача минимизации может быть представлена в виде:

КДНФ Þ СДНФ Þ ТДНФ Þ МДНФ.

Распространение терминологии в отношении нулевого покрытия базируется на понятии имплиценты (как соответствие импликанте) и системы имплицент.

2.14.1 Нахождение множества максимальных кубов
(простых импликант) булевой функции

Рассмотрим процедуру нахождения простых импликант на следующем примере.

Пример 2.18. Минимизация булевой функции методом Квайна-Мак-Класки.

Найти множество простых импликант булевой функции заданной в числовой форме:

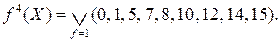
На этом этапе производятся всевозможные склеивания кубов меньшей размерности с целью получения кубов большей размерности. Для сокращения количества операций сравнения кубов на предмет их склеивания целесообразно производить упорядочивание кубов одинаковой размерности путем разделения их на группы по количеству единичных координат. При таком подходе в операцию склеивания могут вступать только кубы, принадлежащие двум соседним группам, то есть такие кубы, количество единичных координат в которых отличается на единицу. Кроме того, рекомендуется проводить нумерацию кубов одинаковой размерности с фиксацией пары склеиваемых кубов при образовании куба большей размерности как результат склеивания. Также по ходу склеивания необходимо осуществлять отметку кубов, вступающих в операцию склеивания. Тогда после завершения операций по склеиванию кубов все неотмеченные кубы будут представлять собой множество максимальных кубов как кубов, не участвовавших ни в одной операции склеивания.

Результат этого этапа представлен в табл. 2.4.

Таблица 2.4. Нахождение множества максимальных кубов

Замечания.

1. При образовании 2-кубов получено два одинаковых 2-куба как результата склеивания двух различных пар соседних 1-кубов. Точно также при образовании 3-кубов должно получаться три одинаковых 3-куба как результата склеивания трех различных пар соседних 2-кубов. Этот факт хорошо согласуется с геометрической интерпретацией кубов небольшой размерности. Действительно, 2-куб представляет собой грань трехмерного куба, которая полностью определяется одной из двух противоположных ребер, соответствующих двум соседним 1-кубам. В свою очередь 3-куб соответствует полному трехмерному кубу, который полностью определяется одной из трех пар противоположных граней, интерпретируемых как геометрические образы двух соседних 2-кубов.

Продолжая аналогию, можно заметить, что при склеивании r-кубов (r³ 3), получается (r+1) одинаковых (r+1)-кубов. Этот факт можно использовать как некоторое подтверждение корректности производимых операций склеивания над кубами.

2. Можно проследить за уменьшением цены покрытий заданной булевой функции, получаемых из кубов различной размерности. Так, для покрытия С_о(f)=K° (f), составленного из исходных 0-кубов, цена составляет: S^a = 9×4 = 36, S ^b= 36+9 = 45. Этому покрытию соответствует КДНФ заданной функции. Так как все 0-кубы отмечены как вступающие в операции склеивания, то кубический комплекс К¹(f) также можно рассматривать в качестве одного из покрытий булевой функции: С₁(f)=К¹(f). Цена этого покрытия: S^a = 10×3 = 30, S^b = 30+10 = 40. Этому покрытию соответствует ДНФ заданной функции:

И, наконец, множество максимальных кубов Z(f) также представляет собой покрытие заданной функции С₂(f)=Z(f) с ценой:

S^a = 1×2+6×3 = 20, S^b = 20+7 = 27.

Этому покрытию соответствует СДНФ вида:

3. При минимизации не полностью определенных булевых функций производится дополнение множества 0-кубов (существенные вершины) булевой функции множеством безразличных наборов N(f) с целью образования кубов большей размерности. Тем самым на этом этапе осуществляется доопределение исходной функции значениями «единица» на безразличных наборах.

Определение ядра покрытия

Для выполнения этого этапа первоначально строится таблица покрытий, строки которой соответствуют максимальным кубам покрытия, а столбцы – существенным вершинам булевой функции. Безразличные наборы аргументов при минимизации не полностью определенной булевой функции в таблице покрытий не участвуют. Тем самым на этом этапе производится доопределение не полностью определенной булевой функции значениями нуля на безразличных наборах аргументов.

Таблица покрытий отображает отношение покрытия между существенными вершинами булевой функции и максимальными кубами. Для этого на пересечении i-ой строки и j-го столбца таблицы делается соответствующая отметка в том случае, если максимальный куб из i-ой строки покрывает существенную вершину из j-го столбца.

Таблица покрытий с соответствующими отметками приведена в виде табл. 2.5.

Замечания.

1. Таблицу покрытий называют также импликантной таблицей в связи с тем, что максимальные кубы соответствуют простым (первичным) импликантам булевой функции, а существенные вершины - конституентам единицы булевой функции.

2. Для полностью определенных булевых функций количество меток в строке таблицы покрытий, соответствующей максимальному кубу размерности r, равно 2^r. Для не полностью определенных функций количество меток может быть меньше 2^r в том случае, если в образовании r-куба участвуют кроме существенных вершин и безразличные наборы.

Для выделения ядра покрытия в таблице покрытий ищутся столбцы, в которых содержится единственная метка. Это означает, что существенная вершина, соответствующая такому столбцу, покрывается только одним из максимальных кубов. В соответствии с этим максимальный куб, который один и только один покрывает некоторую существенную вершину булевой функции, включается в обязательную часть покрытия, называемую ядром.

В табл. 2.5 выделены метки, являющиеся единственными в своих столбцах.

Максимальные кубы	Существенные вершины
				1000	1010	1110
1XX0					´	Ä	Ä	´
000X	´	´
X000	´				´
0X01		´	´
01X1			´	´
X111				´					´
111X								´	´

Таблица 2.5. Таблица покрытий

Как видно из табл. 2.5, в нашем примере кубом ядра будет являться куб: T(f)={1ХХ0}.