
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Кинематика манипулятора и основные задачи кинематики.
Оглавление
1. Кинематика манипулятора и основные задачи кинематики. 2
2. Матрицы элементарных поворотов. 3
3. Матрицы сложных поворотов. 4
4. Матрица поворота вокруг произвольной оси. 5
5. Представление матриц поворота через углы Эйлера. 7
6. Геометрический смысл и свойства матриц поворота. 10
7. Однородные координаты и матрицы преобразования. 11
8. Звенья, сочленения и их параметры. 13
9. Элементарные сочленения. 13
10. Представление Денавита-Хартенберга. 15
11. Уравнения кинематики манипулятора Пума. 16
12. Классификация манипуляторов. 19
13. Обратная задача кинематики. 19
14. Метод обратных преобразований. 20
15. Геометрический подход к решению обратной задачи манипулятора Пума. 23
16. Определение различных конфигураций манипулятора Пума. 24
17. Решение обратной задачи кинематики для первого сочленения манипулятора Пума. 25
18. Решение обратной задачи кинематики для второго сочленения манипулятора Пума. 27
19. Решение обратной задачи кинематики для третьего сочленения манипулятора Пума. 29
20. Решен. обрат. задачи кинем. для посл. трех сочлен. манипул. Пума (общ. полож). 30
21. Решение обратной задачи кинем. для четвертого сочленения манипул. Пума. 31
22. Решение обратной задачи кинематики для пятого сочленения манипулятора Пума. 33
23. Решение обратной задачи кинематики для шестого сочленения манипулятора Пума. 34
24. Уравнения вида конфигурации для определения индикаторов конфигурации манипулятора. 35
25. Динамика манипулятора (общие положения, основные задачи и методы решения) 37
26. Метод Лагранжа-Эйлера. 38
27. Определение скорости произвольной точки звена манипулятора методом Лагранжа-Эйлера. 39
28. Кинет. и потенц. энергия в соответствии с методом Лагранжа-Эйлера. 41
29. Уравнения движения манипулятора в соответствии с методом Лагранжа-Эйлера. 43
30. Уравнения движения манипулятора с вращательными сочленениями в соответствии с методом Лагранжа-Эйлера. 45
31. Уравнения Ньютона-Эйлера для вращающейся системы координат. 47
32. Уравнения Ньютона-Эйлера для подвижной системы координат. 49
Кинематика манипулятора и основные задачи кинематики.
Предметом кинематики манипулятора является аналитическое описание геометрии движения манипулятора относительно некоторой заданной абсолютной системы координат без учёта сил и моментов, порождающих это движение. Таким образом, задачей кинематики является аналитическое описание пространственного расположения манипулятора в зависимости от времени и, в частности, установление связи между значениями присоединённых координат манипулятора и положением и ориентацией его схвата в декартовом пространстве.
Механический манипулятор можно рассматривать как разомкнутую цепь, которая состоит из нескольких твёрдых звеньев, последовательно соединенных вращательными или поступательными сочленениями, приводимых в движение силовыми приводами.
Основные задачи кинематики манипулятора:
1. Для конкретного манипулятора по известному вектору присоединённых углов (обобщённых координат q(t)=(q1(t),q2(t),...,qn(t))g) и заданным геометрическим параметром звеньев (n – число степеней свободы) определить положение и ориентацию схвата манипулятора относительно абсолютной системы координат.
2. При известных геометрических параметрах звеньев найти все возможные векторы присоединённых переменных манипулятора, обеспечивающие заданное положение и ориентацию схвата относительно абсолютной систем координат.
Первую из этих задач принято называть прямой, а вторую – обратной задачей кинематики манипулятора.
| Прямая задача кинематики |
| Параметры звеньев |
| Присоединённые углы (обобщённые координаты) q1(t),q2(t),...,qn(t) |
| Положение и ориентация схвата |
| Параметры звеньев |
| Обратная задача кинематики |
| Присоединённые углы (обобщённые координаты) q1(t),q2(t),...,qn(t) |

Рисунок 2.1. Схема взаимосвязи прямой и обратной задач кинематики
Для описания взаимного пространственного положения двух смежных звеньев используют однородную матрицу преобразования размерностью 4´4.
Матрицы сложных поворотов.
Описание последовательности конечных поворотов относительно основных осей системы OXYZ можно получить путём перемножения матриц элементарных поворотов. Поскольку операция перемножения матриц некоммутативна, здесь существенна последовательность выполнения поворотов.
Например, матрица поворота, представляющего собой результат последовательного выполнения поворотов сначала на угол a вокруг оси OX, затем на угол q вокруг оси OZ, затем на угол j вокруг оси OY имеет вид:
R = R y,j ×R z,q ×R x,a =  =
=
=  , (2-14)
, (2-14)
где Сj = cosj ; Sj = sinj ; Cq = cosq ; Sq = sinq ; Ca = cosa ; Sa = sina.
Она отличается от матрицы, описывающей результат поворота сначала на угол j вокруг оси OY, затем q вокруг оси OZ и, наконец, на угол a относительно оси OX. В этом случае результирующая матрица поворота имеет вид:
R = R x,a ×Rz,q × R y,j =  =
=
=  . (2-15)
. (2-15)
Наряду с вращением относительно осей абсолютной системы координат OXYZ подвижная система отсчёта OUVW может совершать поворот вокруг собственных осей. В этом случае результирующая матрица поворота мб получена с использ следующих правил:
1. Вначале обе системы координат совпадают, и, следовательно, матрица поворота представляет собой единичную матрицу размерностью 3´3.
2. Если подвижная система координат OUVW совершает поворот вокруг одной из основных осей системы OXYZ, матрицу предыдущего результирующего поворота надо умножить слева на соответствующую матрицу элементарного поворота.
3. Если подвижная система координат OUVW совершает поворот вокруг одной из своих основных осей, матрицу предыдущего результирующего поворота надо умножить справа на соответствующую матрицу элементарного поворота.
Пример. Требуется найти матрицу поворота, являющегося результатом последовательного выполнения поворотов сначала на угол j, вокруг оси OY, затем на угол q вокруг оси OW на угол a вокруг оси OU.Решение:
R = R y,j ×I3 ×R w,q ×R u,a =R y,j ×I3 ×R w,q ×R u,a =
=  =
=
=  .
.
Свойства матриц поворота
1. Каждый столбец матрицы поворота представляет собой единичный вектор в направлении соответствующей оси повёрнутой системы отсчёта, заданной своими координатами относительно абсолютной системы координат.
Каждая строка матрицы поворота представляет собой единичный вектор в направлении соответствующей оси абсолютной системы координат, заданной своими координатами относительно повёрнутой системы отсчёта OUVW.
2. Поскольку каждый столбец и строка представляет собой координаты единичного вектора, длина векторов, определяемых строками и столбцами матрицы поворота, равна 1. Детерминант матрицы поворота равен +1 для правосторонней системы отсчёта и -1 – для левосторонней.
3. Поскольку столбцы (строки) матрицы поворота являются векторами, составляющими ортонормированный базис, скалярное произведение векторов, определяемых двумя различными столбцами (строками), равно нулю.
4. Операция обращения матрицы поворота совпадают с операцией транспонирования:R-1 =RT и RRT = I3, где I3 – единичная матрица размерностью 3´3.
Свойства 3 и 4 особенно полезны для проверки результатов умножения двух матриц поворота и при поиске строки или столбца матрицы поворота, в котором сделана ошибка.
7. Однородные координаты и матрицы преобразования.
Поскольку трёхмерная матрица поворота не несёт информации о поступательном перемещении и используемом масштабе, вектор координат р= (рx, рy, рz)T в трёхмерном пространстве дополняют четвёртой координатой (или компонентой) так, что он принимает вид:  = (wрx, wрy, wрz, w)T. Тогда вектор
= (wрx, wрy, wрz, w)T. Тогда вектор  выражен в однородных координатах.
выражен в однородных координатах.
Описание точек трёхмерного пространства однородными координатами позволяет ввести в рассмотрение матричные преобразования, содержащие одновременно поворот, параллельный перенос, изменение масштаба и преобразование перспективы.
В общем случае изображение N-мерного вектора размерностью N+1 называется представлением в однородных координатах. При таком представлении преобразование N-мерного вектора производится в (N+1)-мерном пространстве, а физический N-мерный вектор получается делением однородных координат на (N+1)-ю компоненту  .
.
Так, вектор р = (рx, рy, рz)T положения в трёхмерном пространстве в однородных координатах представляется расширенным вектором (wрx, wрy, wрz, w)T.
Физические координаты связанны с однородными следующим образом:
рx =  , рy=
, рy=  , рz=
, рz=  ,
,
где w – четвёртая компонента вектора однородных координат (масштабирующий множитель).
Если w = 1, то однородные координаты вектора положения совпадают с его физическими координатами.
Однородная матрица преобразования представляет собой матрицу размерностью 4´4, которая преобразует вектор, выраженный в однородных координатах, из одной системы отсчёта в другую.
Однородная матрица преобразования может быть разбита на четыре подматрицы:
Т =  =
=  . (4-1)
. (4-1)
Верхняя левая подматриа размерностью 3×3 представляет собой матрицу поворота; верхняя правая подматрица размерностью 3×1 представляет собой вектор положения начала координат повернутой системы отсчета относительно абсолютной; Нижняя левая подматрица размерностью 1×3 задает преобразование перспективы; четвертый диагональный элемент является глобальным масштабирующим множителем. Однородная матрица преобразования позволяет выявить геометрическую связь между связанной системой отсчёта OUVW и абсолютной системой OXYZ.
Если вектор ртрехмерного пространства выражен в однородных координатах, т.е.  , то, используя понятие матрицы преобразования можно сформировать однородную матрицу преобразования Тпов, задающую преобразование поворота и имеющую размерность 4×4. Однородная матрица поворота получается соответствующим расширением обычной матрицы поворота, имеющей размерность 3×3. Так, однородное представление для матриц (2-12) и (2-13) имеет следующий вид:
, то, используя понятие матрицы преобразования можно сформировать однородную матрицу преобразования Тпов, задающую преобразование поворота и имеющую размерность 4×4. Однородная матрица поворота получается соответствующим расширением обычной матрицы поворота, имеющей размерность 3×3. Так, однородное представление для матриц (2-12) и (2-13) имеет следующий вид:
 ,
,  ,
,
 . (4-2)
. (4-2)
Эти матрицы размерностью 4×4 называются однородными матрицами элементарных поворотов. Однородная матрица преобразования переводит вектор, заданый однородными координатами в системе отсчета OUVW, в абсолютную систему координат OXYZ, т.е. при  :
:
 (4-3)
(4-3)
и  . (4-4)
. (4-4)
Элементарные сочленения.
Механический манипулятор состоит из звеньев, соединенных вращательными или поступательными сочленениями (рис. 3.1). Каждая пара, состоящая из звена и сочленения, обеспечивает одну степень свободы. Следовательно, манипулятор с N степенями свободы содержит N пар «звено-шарнир». Звено 0 соединено с основанием, где обычно размещается инерциальная система координат динамической системы, а последнее звено снабжено рабочим инструментом.
Звенья и сочленения нумеруются по возрастанию от стойки к схвату манипулятора. Каждое звено соединено не более чем с двумя другими так, чтобы не образовывалось замкнутых цепей.
В общем случае два звена соединяются элементарным сочленением, имеющим две соприкасающиеся поверхности, скользящие друг относительно друга.

Рисунок 5.1. Звенья и сочленения манипулятора Пума
Известно всего шесть различных элементарных сочленений: вращательное, поступательное (призматическ), цилиндрическ, сферическ, винтовое и плоское (рис. 5.2.).
Из перечисленных типов сочленений в манипуляторах обычно используются только вращательные и поступательные. В месте соединения двух звеньев определяется ось i-го сочленения (рис. 5.3). Эта ось имеет две пересекающие ее нормали, каждая из которых соответствует одному из звеньев (звена i-1 и звена i), определяется величиной di – расстоянием между этими нормалями, отсчитываемым вдоль оси сочленения.

Рисунок 5.2. Элементарные сочленения
Присоединенный угол i между нормалями измеряется в плоскости, перпендикулярной оси сочленения. Таким образом, di и i можно назвать расстоянием и углом между смежными звеньями. Они определяют относительное положение соседних звеньев.

Рисунок 5.3. Система координат и ее параметры
Звено i (i=1, 2, 3, …., 6) соединено не более чем с двумя звеньями (i-1-м и i+1-м звеньями). Таким образом, в точках соединения i-го звена с двумя соседними определены две оси сочленения. Важное свойство звеньев с точки зрения кинематики состоит в том, что они сохраняют неизменной конфигурацию относительного расположения соседних сочленений, характеризуемую параметрами ai и  i. В качестве параметра ai выбрано кратчайшее расстояние между осями zi-1 и zi i-го и i+1-го сочленений соответственно, измеряемое вдоль их общей нормали. Угол
i. В качестве параметра ai выбрано кратчайшее расстояние между осями zi-1 и zi i-го и i+1-го сочленений соответственно, измеряемое вдоль их общей нормали. Угол  i – угол между осями сочленений, измеряемый в плоскости, перпендикулярной их общей нормали. Таким образом, ai и
i – угол между осями сочленений, измеряемый в плоскости, перпендикулярной их общей нормали. Таким образом, ai и  можно рассматривать соответственно как длину и угол скрутки i–го звена. Эти параметры характеризуют конструктивные особенности i–го звена.
можно рассматривать соответственно как длину и угол скрутки i–го звена. Эти параметры характеризуют конструктивные особенности i–го звена.
Итак, с каждым звеном манипулятора связаны четыре параметра: ai , αi di, i. Если для этих параметров установить правило выбора знаков , то они составят набор, достаточный для описания кинематической схемы каждого звена манипулятора. Эти параметры можно разделить на две пары: параметры звена (ai, αi), которые характеризуют конструкцию звена, и параметры сочленения (di, i), характеризующие относительное положение соседних звеньев
Классификация манипуляторов.
Манипулятор состоит из последовательности твердых тел (или звеньев), первое из которых соединено с опорной стойкой, а последнее снабжено рабочим инструментом. Каждое звено соединено не более чем с двумя другими так, чтобы не образовывалось замкнутых цепей. Соединение двух звеньев – сочленение – имеет только одну степень свободы. С учетом этого ограничения интерес представляет два типа сочленений: вращательное и поступательное. Вращательное сочленение допускает только вращение вокруг некоторой оси; поступательное сочленение обеспечивает поступательное движение вдоль некоторой оси при отсутствии вращения (поступательное движение с вращением имеет место в винтовых сочленениях). Звенья манипулятора участвуют в относительном движении, в результате которого достигается определенное положение и ориентация схвата или инструмента.
Следовательно, рассматривая манипуляторы как некоторые последовательности сочленений и звеньев, их можно классифицировать по типу используемых сочленений и последовательности их расположения в направлении от опорной стойки к схвату. При таком подходе манипулятор Пума следует отнести к классу 6В, а манипулятор «Электроника» - к классу 2П-В-П-В. Здесь «В» обозначает вращательное, а «П» – поступательное сочленение.
Обратная задача кинематики
В этом разделе рассматривается обратная задача кинематики шестизвенного манипулятора. Необходимо по заданной матрице 0T6 положения и ориентации схвата шестизвенного манипулятора и известным параметрам его звеньев и сочленений определить присоединенные параметры  манипулятора, обеспечивающие заданное положение схвата.
манипулятора, обеспечивающие заданное положение схвата.
Для того, чтобы решение обратной задачи кинематики было получено в явном виде, необходимо, чтобы конструкция робота удовлетворяла одному из двух условий:
1. Оси трех смежных сочленений пересекаются в одной точке.
2. Оси трех смежных сочленений параллельны между собой.
Из равенства (4-2) следует вид матрицы манипулятора T:
T6=  =0A1 1A2 2A3 3A4 4A5 5A6. (6-7)
=0A1 1A2 2A3 3A4 4A5 5A6. (6-7)
Из равенства (4-7) видно, что матрица T является функцией синусов и косинусов углов 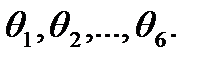 Приравнивая элементы матриц в левой и правой частях матричного уравнения (4-7), получаем, например, для манипулятора Пума двенадцать уравнений (4-3) – (4-6) относительно шести неизвестных (присоединенных углов). Поскольку число уравнений превышает число переменных, можно сразу сделать вывод о том, что решение обратной задачи кинематики для манипулятора Пума не единственно. Мы рассмотрим два метода решения обратной задачи кинематики: метод обратных преобразований в эйлеровых координатах и геометрический подход, выгодно отличающийся наглядностью.
Приравнивая элементы матриц в левой и правой частях матричного уравнения (4-7), получаем, например, для манипулятора Пума двенадцать уравнений (4-3) – (4-6) относительно шести неизвестных (присоединенных углов). Поскольку число уравнений превышает число переменных, можно сразу сделать вывод о том, что решение обратной задачи кинематики для манипулятора Пума не единственно. Мы рассмотрим два метода решения обратной задачи кинематики: метод обратных преобразований в эйлеровых координатах и геометрический подход, выгодно отличающийся наглядностью.
14. Метод обратных преобразований.
Задача состоит в том, чтобы, зная трехмерную матрицу поворота и учитывая равенство (2-2), представляющее собой выражение этой матрицы через углы Эйлера:
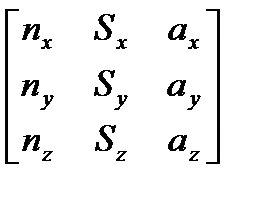 =
= 
 , (6-8)
, (6-8)
где  и
и  ,
,
определить соответствующие значения углов  Записывая это матричное уравнение в форме уравнений для отдельных элементов, получим:
Записывая это матричное уравнение в форме уравнений для отдельных элементов, получим:
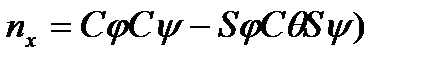 ; (6-9а)
; (6-9а)
 ; (6-9б)
; (6-9б)
 ; (6-9в)
; (6-9в)
 ; (6-9г)
; (6-9г)
 ; (6-9д)
; (6-9д)
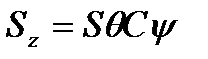 ; (6-9е)
; (6-9е)
 ; (6-9ж)
; (6-9ж)
 ; (6-9з)
; (6-9з)
 . (6-9и)
. (6-9и)
Из уравнений (6-9и), (6-9е) и (6-9з) получаем, что решение всей системы уравнений (6-9а) – (6-9и) имеет следующий вид:
 , (6-10)
, (6-10) 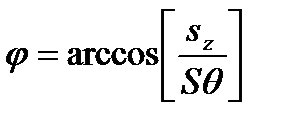 , (6-11)
, (6-11)  . (6-12)
. (6-12)
Полученное решение неустойчиво и плохо обусловлено по следующим причинам:
1. Функция arccos неудобна тем, что точность вычисления ее значения зависит от этого значения.
2. В точках, где sin (  ) принимает близкие к нулю значения, т.е. при
) принимает близкие к нулю значения, т.е. при  »0° или при
»0° или при  »180°, равенства (6-11) и (6-12) либо не определены, либо дают низкую точность вычислений.
»180°, равенства (6-11) и (6-12) либо не определены, либо дают низкую точность вычислений.
Более устойчивый способ определения углов Эйлера для вычисления угла  , значения которого лежат в пределах -p£
, значения которого лежат в пределах -p£  £p, использует функции арктангенса ATAN2(y,x), вычисляющий значение arctg(y/x) с учетом принадлежности аргумента соответствующему квадранту:
£p, использует функции арктангенса ATAN2(y,x), вычисляющий значение arctg(y/x) с учетом принадлежности аргумента соответствующему квадранту:
 (6-13)
(6-13)
Применяя такую обратную тригонометрическую функцию двух аргументов, рассмотрим общее решение.
Элементы матрицы в левой части матричного уравнения (6-8) заданы, а элементы матриц, стоящих в правой части этого уравнения, неизвестны и зависят от  Умножая слева матричное уравнение (6-8) на
Умножая слева матричное уравнение (6-8) на  , переносим неизвестную
, переносим неизвестную  в левую часть, оставляя в правой неизвестные
в левую часть, оставляя в правой неизвестные 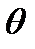 и
и  , и тем самым получаем:
, и тем самым получаем:
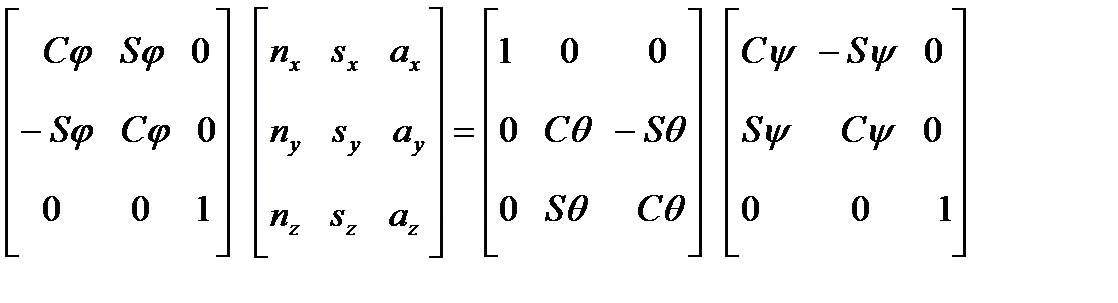 ,
,
или
 . (6-14)
. (6-14)
Из равенства элементов (1, 3) (элементов, находящихся на пересечении 1-й строки и 3-го столбца матрицы) в правой и левой частях уравнения (6-14) имеем:
 , (6-15)
, (6-15)
что в свою очередь дает

 . (6-16)
. (6-16)
Из равенства элементов (1, 1), (1, 2) в правой и левой частях следует:
 , (6-17а)
, (6-17а)
 , (6-17б)
, (6-17б)
что позволяет найти  :
:
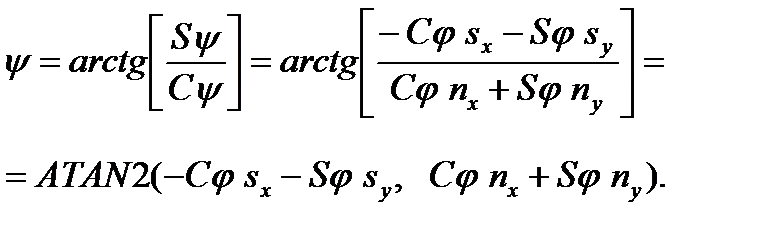 (6-18)
(6-18)
Приравнивая элементы (2, 3), (3, 3) матриц в левой и правой частях уравнения, получаем:
 ,
,
 , (6-19)
, (6-19)
что позволяет найти  :
:
 . (6-20)
. (6-20)
Таким образом, рассмотренный способ состоит в умножении исходного уравнения слева и справа на неизвестную матрицу обратного преобразования. Этот способ дает общий подход к решению обратной задачи кинематики. Но не дает точного ответа, каким образом выбрать из нескольких существующих решений одно, соответствующее требуемой конфигурации манипулятора. В этом вопросе приходится полагаться на интуицию исследователя. Для нахождения решения обратной задачи кинематики по заданной матрице манипулятора более пригодным является геометрический подход, дающий также и способ выбора единственного решения для конкретной конфигурации манипулятора.
Решение для первого сочленения
Проецируя, как показано на рис. 7.1, вектор р на плоскость x0, y0, получаем следующие уравнения для определения угла  :
:
 ,
, 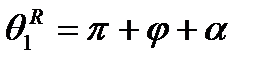 , (7-8)
, (7-8)
 ,
,  , (7-9)
, (7-9)
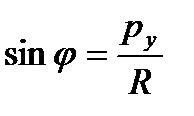 ,
,  , (7-10)
, (7-10)
 ,
, 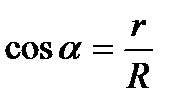 , (7-11)
, (7-11)
 где индексы L и R означают ЛЕВУЮ и ПРАВУЮ конфигурацию манипулятора.
где индексы L и R означают ЛЕВУЮ и ПРАВУЮ конфигурацию манипулятора.
Рисунок 7.1. Решение для 1-го сочленения
Из уравнений (7-8) – (7-11) получаем значения функций синуса и косинуса угла 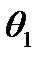 для ЛЕВОЙ/ПРАВОЙ конфигурации манипулятора:
для ЛЕВОЙ/ПРАВОЙ конфигурации манипулятора:
 , (7-12)
, (7-12)
 , (7-13)
, (7-13)
 , (7-14)
, (7-14)
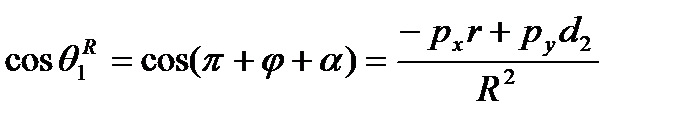 . (7-15)
. (7-15)
Объединив равенства (7-12) – (7-15) и используя индикатор РУКА для учета ЛЕВОЙ/ПРАВОЙ конфигурации манипулятора, получаем значения функций синуса и косинуса угла  в следующем виде:
в следующем виде:
 , (7-16)
, (7-16)
 . (7-17)
. (7-17)
В этих равенствах используется положительное значение квадратного корня, а индикатор РУКА определен равенством (7-2). Для вычисления  , лежащего в пределах
, лежащего в пределах  , воспользуемся функцией арктангенса, определенной равенством (6-13). Из равенств (7-16) и (7-17) с учетом равенства (6-13) получаем следующую формулу для определения
, воспользуемся функцией арктангенса, определенной равенством (6-13). Из равенств (7-16) и (7-17) с учетом равенства (6-13) получаем следующую формулу для определения  :
:
 . (7-18)
. (7-18)
Метод Лагранжа-Эйлера.
Полное описание движения манипулятора можно получить, применяя метод Лагранжа-Эйлера для неконсервативных систем. Описав кинематику манипулятора с помощью матричного представления Денавита-Хартенберга, можно получить уравнение динамики. Такое совместное использование Д-Х-представления и метода Лагранжа приводит к компактной векторно-математической форме уравнений движения, удобной для аналитического исследования и допускающей реализацию на ЭВМ.
Вывод уравнений динамики движения манипулятора основан на следующем:
1. На описании взаимного пространственного расположения систем координат i-го и (i-1)-го звеньев с помощью матрицы преобразования однородных координат 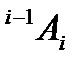 . Эта матрица преобразует координаты произвольной точки относительно i-й системы координаты этой же точки относительно (i-1)-й системы координат.
. Эта матрица преобразует координаты произвольной точки относительно i-й системы координаты этой же точки относительно (i-1)-й системы координат.
2. На использовании уравнения Лагранжа-Эйлера:
 ;
; 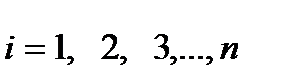 , (9-9)
, (9-9)
где L-функция Лагранжа (L=K-P);
K-полная кинетическая энергии манипулятора;
P-полная потенциальна энергия манипулятора
 -обобщённые координаты манипулятора;
-обобщённые координаты манипулятора;
 -первая производная по времени обобщённых координат;
-первая производная по времени обобщённых координат;
 -обобщённые силы (или моменты), создаваемые в i-м сочленении для реализации заданного движения i-го звена.
-обобщённые силы (или моменты), создаваемые в i-м сочленении для реализации заданного движения i-го звена.
Для того, чтобы воспользоваться уравнением Лагранжа-Эйлера, необходимо выбрать систему обобщённых координат. Обобщённые координаты представляют собой набор координат, обеспечивающий, полное описание положения рассматриваемой физической системы в абсолютной системе координат. Существуют различные системы обобщенных координат, пригодные для описания простого манипулятора с вращательными и поступательными сочленениями. Однако, поскольку углы поворотов в сочленениях непосредственно доступны измерению с помощью потенциометров или других датчиков, то они составляют наиболее естественную систему обобщенных координат. В этом случае обобщённые координаты совпадают с присоединенными переменными манипулятора. В частности, если i-е сочленение вращательное, то  , если же i-е сочленение поступательное, то
, если же i-е сочленение поступательное, то  .
.
Оглавление
1. Кинематика манипулятора и основные задачи кинематики. 2
2. Матрицы элементарных поворотов. 3
3. Матрицы сложных поворотов. 4
4. Матрица поворота вокруг произвольной оси. 5
5. Представление матриц поворота через углы Эйлера. 7
6. Геометрический смысл и свойства матриц поворота. 10
7. Однородные координаты и матрицы преобразования. 11
8. Звенья, сочленения и их параметры. 13
9. Элементарные сочленения. 13
10. Представление Денавита-Хартенберга. 15
11. Уравнения кинематики манипулятора Пума. 16
12. Классификация манипуляторов. 19
13. Обратная задача кинематики. 19
14. Метод обратных преобразований. 20
15. Геометрический подход к решению обратной задачи манипулятора Пума. 23
16. Определение различных конфигураций манипулятора Пума. 24
17. Решение обратной задачи кинематики для первого сочленения манипулятора Пума. 25
18. Решение обратной задачи кинематики для второго сочленения манипулятора Пума. 27
19. Решение обратной задачи кинематики для третьего сочленения манипулятора Пума. 29
20. Решен. обрат. задачи кинем. для посл. трех сочлен. манипул. Пума (общ. полож). 30
21. Решение обратной задачи кинем. для четвертого сочленения манипул. Пума. 31
22. Решение обратной задачи кинематики для пятого сочленения манипулятора Пума. 33
23. Решение обратной задачи кинематики для шестого сочленения манипулятора Пума. 34
24. Уравнения вида конфигурации для определения индикаторов конфигурации манипулятора. 35
25. Динамика манипулятора (общие положения, основные задачи и методы решения) 37
26. Метод Лагранжа-Эйлера. 38
27. Определение скорости произвольной точки звена манипулятора методом Лагранжа-Эйлера. 39
28. Кинет. и потенц. энергия в соответствии с методом Лагранжа-Эйлера. 41
29. Уравнения движения манипулятора в соответствии с методом Лагранжа-Эйлера. 43
30. Уравнения движения манипулятора с вращательными сочленениями в соответствии с методом Лагранжа-Эйлера. 45
31. Уравнения Ньютона-Эйлера для вращающейся системы координат. 47
32. Уравнения Ньютона-Эйлера для подвижной системы координат. 49
Кинематика манипулятора и основные задачи кинематики.
Предметом кинематики манипулятора является аналитическое описание геометрии движения манипулятора относительно некоторой заданной абсолютной системы координат без учёта сил и моментов, порождающих это движение. Таким образом, задачей кинематики является аналитическое описание пространственного расположения манипулятора в зависимости от времени и, в частности, установление связи между значениями присоединённых координат манипулятора и положением и ориентацией его схвата в декартовом пространстве.
Механический манипулятор можно рассматривать как разомкнутую цепь, которая состоит из нескольких твёрдых звеньев, последовательно соединенных вращательными или поступательными сочленениями, приводимых в движение силовыми приводами.
Основные задачи кинематики манипулятора:
1. Для конкретного манипулятора по известному вектору присоединённых углов (обобщённых координат q(t)=(q1(t),q2(t),...,qn(t))g) и заданным геометрическим параметром звеньев (n – число степеней свободы) определить положение и ориентацию схвата манипулятора относительно абсолютной системы координат.
2. При известных геометрических параметрах звеньев найти все возможные векторы присоединённых переменных манипулятора, обеспечивающие заданное положение и ориентацию схвата относительно абсолютной систем координат.
Первую из этих задач принято называть прямой, а вторую – обратной задачей кинематики манипулятора.
| Прямая задача кинематики |
| Параметры звеньев |
| Присоединённые углы (обобщённые координаты) q1(t),q2(t),...,qn(t) |
| Положение и ориентация схвата |
| Параметры звеньев |
| Обратная задача кинематики |
| Присоединённые углы (обобщённые координаты) q1(t),q2(t),...,qn(t) |

Рисунок 2.1. Схема взаимосвязи прямой и обратной задач кинематики
Для описания взаимного пространственного положения двух смежных звеньев используют однородную матрицу преобразования размерностью 4´4.
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...