
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Вероятностные методы в строительной механике
Шумилов К. А.
Козлова Е. М.
Вероятностные методы в строительной механике
Часть 1
Учебное пособие
УДК 004.92:378 (075.8)
Рецензент: профессор Б. Г. Вагер (СПбГАСУ).
Шумилов К. А., Козлова Е. М.
Вероятностные методы в строительной механике: / учебное пособие / К. А. Шумилов; СПбГАСУ. – СПб., 2015. – с.
ISBN
Предлагаемое учебное пособие представляет собой практикум по использованию методов теории вероятностей в строительстве. Обучение предполагает наличие знаний по строительной механике. Основная задача автора – научить использовать вероятностные методы для анализа качества строительных проектов.
Предназначено для студентов технических специальностей.
Рекомендовано Редакционно-издательским советом.
ISBN © К. А. Шумилов, Козлова Е. М. 2015
© Санкт-Петербургский государственный архитектурно-строительный университет, 2015
Оглавление
1. Задачи теории вероятностей в строительстве.................................................... 3
2. Основные положения теории вероятностей....................................................... 5
3. Характеристики распределения случайных величин...................................... 10
4. Некоторые наиболее важные законы распределения..................................... 20
5. Случайные функции......................................................................................... 24
6. Приближенные методы нахождения распределения функций случайных велчин 31
7. Вероятность редких событий (появление случайного события A за время T) 32
8. Простейшие модели надежности...................................................................... 33
Литература............................................................................................................ 40
ЗАДАЧИ ТЕОРИИ ВЕРОЯТНОСТЕЙ В СТРОИТЕЛЬСТВЕ.
Основные положения теории вероятностей
ИСПОЛЬЗУЕМЫЕ ДЛЯ РЕШЕНИЯ ЗАДАЧ ТЕОРИИ НАДЕЖНОСТИ
СТРОИТЕЛЬНЫХ КОНСТРУКЦИЙ
Событие - качественный или количественный результат опыта, осуществляемого при определенных условиях. Например, событие - попадание предела текучести стали  в интервал от 240 до 260 МПа. Событие может быть случайным, достоверным или невозможным. Объективная математическая оценка возможности реализации случайного события - вероятность. Вероятность есть объективная мера возможности наступления события независимо от того, является ли оно массовым или нет. В жизни все (полуинтуитивно) применяют вероятностные оценки будущим событиям и весьма успешно.
в интервал от 240 до 260 МПа. Событие может быть случайным, достоверным или невозможным. Объективная математическая оценка возможности реализации случайного события - вероятность. Вероятность есть объективная мера возможности наступления события независимо от того, является ли оно массовым или нет. В жизни все (полуинтуитивно) применяют вероятностные оценки будущим событиям и весьма успешно.
Частота события А (статистическая вероятность).
 ,
,
где  - число опытов, в которых наблюдается событие А;
- число опытов, в которых наблюдается событие А;
n - общее число опытов.
Значения  - случайны.
- случайны.
 ,
,
где  - математическая вероятность, являющаяся достоверной величиной, т.е. вероятность того, что при n®¥
- математическая вероятность, являющаяся достоверной величиной, т.е. вероятность того, что при n®¥  равна 1.
равна 1.
 .
.
При  вероятность
вероятность 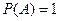 , при
, при  соответственно
соответственно  .
.
События несовместны в данном испытании, если никакие два из них не могут появиться вместе. (Например, появление цифр от 1 до 6 на игральном кубике).
Случайные события совместны, если при данном испытании могут произойти два эти события.
 Если события А и В несовместны, то вероятность появления или события А или события В:
Если события А и В несовместны, то вероятность появления или события А или события В:
 (1.2)
(1.2)
или в общем виде  (1'.2).
(1'.2).
Характеристики распределения случайных величин
Одномерная случайная величина
 С. в. Х (одномерная) - величина, которая может принять различные вероятные значения х на некотором интервале (-¥£х£¥), т.е. х - возможное значение с.в. Х.
С. в. Х (одномерная) - величина, которая может принять различные вероятные значения х на некотором интервале (-¥£х£¥), т.е. х - возможное значение с.в. Х.
С. в. может быть дискретной и непрерывной. Вероятностные свойства с.в. Х характеризуются интегральной функцией распределения Р(x). Значение функции Р(x) равно вероятности обнаружить с.в. Х<х (или, что то же, на интервале ‑¥, х) т.е. Р(x)=Prob(X<x), где х - конкретная детерминированная величина.
Если с.в. Х может принимать лишь дискретные значения х1, х2,...хn с вероятностями р1, р2,...рn, то функция распределения представляет собой сумму вероятностей тех значений хk, которые меньше х.
 . (12.3)
. (12.3)
На рисунке Prob(X£x3)=Р(х3)=0,5, (т.е. Х=х1 или Х=х2 или Х=х3). Prob(X=x4)=0,6-0,5=0,1 (скачок равен вероятности появления значения х4).
 Функция распределения числа m наступления события в последовательности n независимых испытаний (согласно формуле (11.2)).
Функция распределения числа m наступления события в последовательности n независимых испытаний (согласно формуле (11.2)).
Биномиальный закон распределения:
 (13.3)
(13.3)
 .
.
Если с.в. Х непрерывна, то функция распределения имеет вид, показанный на рисунке.
Свойства функции распределения:
1) Р(х) - неубывающая функция аргумента х
(т.е. при x2>x1 P(x2)=Prob(X<x2)>P(x1)=Prob(X<x1));
2) При x=-¥ P(x)=0;
3) При x=+¥ P(x)=1;
4) Prob(x1<X£x2)=P(x2)-P(x1) (14.3);
5) Prob(X=x1)=0. Вероятность обнаружить число, например 241.000...¥ равно 0. Однако, делая измерения, мы округляем значения, тем самым, увеличивая вероятность их появления. Например, округленное 241.0 содержит значения от 240.9500...¥ до 241.04999... ¥ и вероятность попадания числа в этот интервал не равна 0.
 Распределение с.в. Х характеризуется также функцией плотности распределения с.в. Для дискретных значений с.в. функция плотности распределения может задаваться таблично. График функции р(х)=рi при x=xi изображен на рис. .
Распределение с.в. Х характеризуется также функцией плотности распределения с.в. Для дискретных значений с.в. функция плотности распределения может задаваться таблично. График функции р(х)=рi при x=xi изображен на рис. .
 Т.к. возможные значения xi с.в. образуют полную группу несовместных событий (т.е. в каждом из n испытаниях с.в. обязательно примет одно из значений xi с определенной вероятностью), то
Т.к. возможные значения xi с.в. образуют полную группу несовместных событий (т.е. в каждом из n испытаниях с.в. обязательно примет одно из значений xi с определенной вероятностью), то  , где n - число испытаний.
, где n - число испытаний.
Для непрерывной с.в. функция плотности распределения имеет вид, показанный на рисунке.
Если функция распределения с.в. Р(х) - непрерывна, то  (15.3)
(15.3)
или  . По непрерывной кривой плотности распределения, в отличие от дискретной, вероятность обнаружить точное число х2 равна нулю. При помощи функции р(х) вероятность обнаружить с.в. Х в бесконечно малом интервале x<X<x+dx равна Prob(x<X<x+dx)=p(x)dx (площадь прямоугольника, dx®0). То же в конечном интервале x1<X<x2:
. По непрерывной кривой плотности распределения, в отличие от дискретной, вероятность обнаружить точное число х2 равна нулю. При помощи функции р(х) вероятность обнаружить с.в. Х в бесконечно малом интервале x<X<x+dx равна Prob(x<X<x+dx)=p(x)dx (площадь прямоугольника, dx®0). То же в конечном интервале x1<X<x2:
 (16.3)
(16.3)
(Геометрически это заштрихованная площадь под кривой плотности распределения).
Из (15) следует, что  (17.3),
(17.3),
поэтому функцию распределения называют еще интегральной функцией распределения.
Свойства функции плотности распределения:
1) Плотность распределения вероятностей - неотрицательная функция р(х)³0.
2)  (18.3),
(18.3),
что эквивалентно Р(¥)=1.
3) Размерность р(х) обратная размерности с.в., а Р(х) - безразмерна.
4) Числовые характеристики распределения
Математическое ожидание с.в. Х :
- дискретной
 (19.3)
(19.3)
при этом  (М(x) - случайна при n¹¥).
(М(x) - случайна при n¹¥).
- непрерывной
 (20.3).
(20.3).
Математическое ожидание  - достоверная величина, т.к. вероятность того, что при n=¥ испытаниях мы получим среднее арифметическое М(X)=
- достоверная величина, т.к. вероятность того, что при n=¥ испытаниях мы получим среднее арифметическое М(X)= 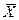 равна 1.
равна 1.
М(с)=с, М(сx) = сМ(x), где с – неслучайное число.
Для независимых с.в. Х1 и Х2
М(x1+x2)=М(x1)+М(x2), М(x1x2)=М(x1)М(x2), М(x2)=[М(x)]2+D(x).
К математическому ожиданию стремится среднее арифметическое наблюдаемых значений с.в. при количестве испытаний n®¥. Геометрически м.о. – это абсцисса ц. т. площади под кривой плотности распределения. Размерность м.о. совпадает с размерностью с.в.
Дисперсия с.в. Х - м.о. квадрата отклонения с.в. Х от ее м.о. (центра распределения):
D(x)=M[x-M(x)]2=M(x2)-M2(x),
т.к. M[x-M(x)]2=M[x2-2xM(x)+M2(x)]=M(x2)-2M2(x)+M2(x),
M[2xM(x)]=2M2(x) и M[M(x)]=M(x).
Дисперсия дискретной с.в. Х
 (21.3)
(21.3)
случайна при n¹¥.
Дисперсия непрерывной с.в. Х:
 (22.3),
(22.3),
(дисперсия непрерывной с.в. - достоверна).
 - математическое ожидание.
- математическое ожидание.
Дисперсия характеризует разброс с.в. вокруг ее среднего значения (математического ожидания).
D(c)=0,
D(cx)=c2D(x),
D(c+x)=D(x).
Доказательство.
D(cx)=M[cx-M(cx)]2=M[c2x2-2cxM(cx)+M2(cx)]=
c2M(x2)-M[2c2xM(x)]+M[c2M2(x)]=
c2M(x2)-2c2M2(x)+c2M2(x)=
c2[M(x2)-M2(x)]=c2D(x). D(c+x)=
M[c+x-M(c+x)]2=M[c+x-c-M(x)]2=M[x-M(x)]2=D(x).
Для независимых с.в. Х1 и Х2 D(x1±x2)=D(x1)+D(x2).
Геометрически дисперсия – это центральный момент инерции площади под кривой плотности распределения. Размерность дисперсии - квадрат размерности с.в.
Среднеквадратическое отклонение (стандарт):  .
.
Асимметрия непрерывной с.в. Х:
 (23.3).
(23.3).
Если с.в. Х распределена симметрично относительно своего м.о., то А(х)=0.
Коэффициент изменчивости (вариации) с.в. Х - отношение стандарта к м.о.:
 (24.3).
(24.3).
Функции случайных величин
Функция с.в. будет также случайной величиной Y=j(X). Ее распределение соответствует распределению аргумента, но с измененной шкалой абсцисс. P(y)=Prob(Y<y)=Prob(j(X)<y).
 (36.3)=(17.3),
(36.3)=(17.3),
где y(y) - функция обратная j(х) (замена подинтегрального выражения x=y(y), dx=y¢(y)dy).
Если Y=j(X), где j(X) - монотонная функция своего аргумента, то распределение Y определяется тем, что вероятность нахождения y в пределах y1<Y<y2 равна вероятности неравенства х1<X<x2,
где y1=j(x1) и y2=j(x2).
М.о. и дисперсия с.в. Y:
 (37.3)=(20.3) и (22.3).
(37.3)=(20.3) и (22.3).
Доказательство(37.3): 
Для линейной функции Y=aX+b из (37.3) и (18.3) следует
 и D(Y)=a2D(X) (38.3).
и D(Y)=a2D(X) (38.3).
Доказательство (38):  .
.
Для функции Z=j(X,Y) двух случайных аргументов м.о. и дисперсия  (39.3).
(39.3).
Если Z=j(X,Y)=X+Y и X и Y - независимы, то м.о.  и дисперсия суммы независимых с.в. величин D(Z)=D(X)+D(Y).
и дисперсия суммы независимых с.в. величин D(Z)=D(X)+D(Y).
Плотность распределения непрерывной с.в. Y, связанной монотонной функциональной зависимостью Y=j(X) с непрерывной с.в. Х:
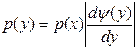 или
или  (40.3),
(40.3),
где x=y(y) - функция обратная y=j(x).
Для линейной функции y=ax+b из (40) следует
p(y)=(1/a)p(x) (40¢.3).
Если Y=j(X/R) и p(x/r) - условная плотность вероятности с.в. Х, входящей в систему (X,R), то условная плотность вероятности с.в. Y -  ,
,
где y(y/r) - функция обратная Y=j(X/R), а безусловная плотность вероятности с.в. Y:
 ,
,
где p(r) - плотность вероятности с.в. R.
Если имеются функции с.в. U=U(X,Y) и V=V(X,Y), то, зная совместную плотность распределения p(x,y), совместная плотность распределения U и V:
 (41.3)
(41.3)
(в скобках - Якобиан  ).
).
Матожидания:  (42.3),
(42.3),
дисперсия  ,
,
корреляционный момент  .
.
В случае линейного преобразования U=a1X+b1Y+c1 и V=a2X+b2Y+c2  по (41.3) и (42.3) имеем:
по (41.3) и (42.3) имеем:
 (43.3),
(43.3),
 и
и  (44.3).
(44.3).
Дисперсия 
Доказательство (44)

Запишем еще раз дисперсии и корреляционные моменты:
 ,
,  ,
,  (доказать самостоятельно).
(доказать самостоятельно).
Зная плотность распределения p(U,V), где U=U(X,Y) и V=V(X,Y), можно определить плотность распределения p(U) или p(V):  .
.
Пример(стр.23 [7]). Стержень нагружен изгибающим моментом Mb и крутящим моментом Mt, и есть их совместная плотность вероятности pq(Mb,Mt). Кроме того, моменты Mb и Mt стохастически независимы и подчиняются центрированному нормальному распределению:
 ,
,
где sb и st – стандарты Mb и Mt.
Опасное состояние стержня достигается при превышении некоторой функцией этих моментов предельного значения Mr>Mr,lim, зависящего от свойств материала и геометрии сечения стержня. Например, для стержня круглого сечения из пластического материала эта функция может быть взята в виде  , где Mr – приведенный момент, определенный в соответствии с критерием текучести, основанном на наибольших касательных напряжениях.
, где Mr – приведенный момент, определенный в соответствии с критерием текучести, основанном на наибольших касательных напряжениях.
Касательное напряжение от крутящего момента  , где Ir - полярный момент круглого сечения, y – радиус окружности, содержащей рассматриваемую точку, t = tmax при y=r (r – радиус стержня). Нормальное напряжение от изгибающего момента
, где Ir - полярный момент круглого сечения, y – радиус окружности, содержащей рассматриваемую точку, t = tmax при y=r (r – радиус стержня). Нормальное напряжение от изгибающего момента  . Для расчета надежности стержня необходимо знать плотность вероятности pu(Mr) приведенного момента Mr.
. Для расчета надежности стержня необходимо знать плотность вероятности pu(Mr) приведенного момента Mr.
Перейдем к полярным координатам, положив  , где 0£q£2p. Согласно (41.3) совместная плотность распределения с. в. Mr и q:
, где 0£q£2p. Согласно (41.3) совместная плотность распределения с. в. Mr и q:
 .
.
Используя  и замечая, что якобиан преобразования
и замечая, что якобиан преобразования  ,
,
найдем

Плотность распределения вероятности pu(Mr) определяется интегрированием полученной формулы по углу q:  . Используя формулу анализа
. Используя формулу анализа  , где
, где  - функция Бесселя мнимого аргумента нулевого порядка, получим окончательно
- функция Бесселя мнимого аргумента нулевого порядка, получим окончательно  .
.
Если дисперсии моментов Mb и Mt одинаковы, т.е. sb=st=s, то I0(0)=1 и  . При этом приведенный момент подчиняется распределению Рэлея.
. При этом приведенный момент подчиняется распределению Рэлея.
СЛУЧАЙНЫХ ВЕЛИЧИН
Нормальное распределение
Плотность распределения:  (45.4).
(45.4).
Точки перегиба кривой плотности распределения:  и
и  .
.
 Функция распределения:
Функция распределения:
 (46.4),
(46.4),
где  - м.о., s(х) – стандарт.
- м.о., s(х) – стандарт.
Чем больше s(х), тем ниже и шире кривая плотности распределения.
Плотность n-мерного нормального распределения:  , где D - определитель корреляционной матрицы
, где D - определитель корреляционной матрицы  , а Ajl – алгебраическое дополнение элемента kjl-того определителя.
, а Ajl – алгебраическое дополнение элемента kjl-того определителя.
Р(х) можно выразить через интеграл вероятности Гаусса
 , (47.4)
, (47.4)
 (48.4).
(48.4).
Функция (47) – нечетная (Ф(-z) = - Ф(z)), имеются таблицы ее значений.
Вероятность попадания с.в. Х в интервал (a,b) –
 (49.4).
(49.4).
Если b-a =6 s(X), то вероятность того, что с.в. Х окажется в интервале  равна 0.9973. Линейные функции с.в., подчиняющиеся нормальным законам распределения, имеют также нормальный закон распределения.
равна 0.9973. Линейные функции с.в., подчиняющиеся нормальным законам распределения, имеют также нормальный закон распределения.
Как показал Ляпунов в случае, если число n безгранично увеличивается, кривая плотностей вероятностей суммы не зависит от кривых плотностей вероятностей, слагаемых при некоторых предположениях, и представляет собой нормальную кривую (45.4).
Условия: слагаемые величины х=х1+х2+...+хn (xi, i=1, 2...n) в среднем одного порядка и одного порядка некоторые характеристики слагаемых - вторые и третьи моменты. Т.о. если с.в. образуется из суммы большого числа независимых, неограниченных случайных переменных факторов, то ее закон - близок к нормальному, т.е. в действительности многие переменные представляют собой результат простого суммирования многих независимых факторов.
Закон больших чисел:
 .
.
Усеченный нормальный закон
Если известны границы возможных значений с.в. (a,b), то

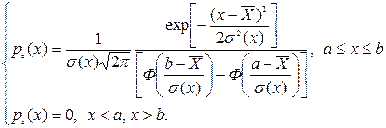 (50.4).
(50.4).
Закон используется для описания реальных величин, распределенных нормально (например, не могущих принимать отрицательные значения).
Распределение Вейбулла
 В теории хрупкого разрушения и других отраслях техники нашло применение распределение Вейбулла. Интегральная кривая распределения:
В теории хрупкого разрушения и других отраслях техники нашло применение распределение Вейбулла. Интегральная кривая распределения:
 (54.4).
(54.4).
Плотность распределения:
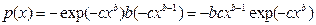 (55.4).
(55.4).
В выражения для числовых характеристик распределения Вейбулла входит гамма-функция
 (56.4),
(56.4),
которая табулирована в математических справочниках.
Распределение Пуассона
Это дискретное распределение описывает число событий, происходящих в одинаковых промежутках времени при условии, что события происходят независимо одно от другого с постоянной интенсивностью. Вероятность того, что с.в. Х примет значение, равное m (m – целое число):
 (65.4)
(65.4)
Распределение зависит от одного параметра l, называемого пуассоновским потоком.
Существуют некоторые недостатки при описании реальных с.в.: так в некоторых законах с.в. может принимать отрицательные значения (нормальный закон), хотя этими законами описываются изначально только положительные величины (предел текучести стали и т.д.). Кроме того, теоретические распределения допускают, хотя и с малой вероятностью, возможность сколь угодно больших отклонений с.в. от среднего значения.
Все теоретические закономерности и законы теории вероятностей относятся к идеальным схемам. Применяемые обычно теоретические законы распределения относятся к ситуациям с неограниченным нарастанием числа случайных факторов или с неограниченным повторением некоторого явления и имеют характер предельных закономерностей, к которым приближаются реальные распределения.
Кроме перечисленныхиспользуются и другие распределения – Пирсона 3-го рода, Рэлея, Максвелла, Пирсона 2-го рода, c2 (хи-квадрат), Стьюдента, Фишера и т.д.
СЛУЧАЙНЫЕ ФУНКЦИИ
Примеры корреляционных функций.
1)  (из (2) при b®0); 2)
(из (2) при b®0); 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  (из (3) при b®0); 6)
(из (3) при b®0); 6)  (из (4) при b®0).
(из (4) при b®0).
На графиках a = 1, b = 5, s = 1.

a - характеризует быстроту убывания корреляционной связи между ординатами с.ф. при увеличении разности аргументов этих ординат t.
a/b - характеризует "степень нерегулярности процесса". При малом a/b ординаты процесса оказываются сильно коррелированными и реализация процесса похожа на синусоиду; при большом a/b периодичность с частотой b становится незаметной.
Корреляционные функции 4 и 6 – не имеют производных при t=0. Соответствующие спектральные плотности:
2)  ;
;
3)  ;
;
4)  ;
;
6)  .
.
Чтобы найти корреляционную функцию интеграла (производной) от с.ф., нужно дважды проинтегрировать (продифференцировать) корреляционную функцию исходной с.ф. сначала по одному, затем по другому аргументу:
 (71.5).
(71.5).
Формула (71) для стационарной функции примет вид:
 .
.
Корреляционная функция с.ф. и ее производной  . Для дифференцируемого стационарного процесса ордината с.ф. и ее производной, взятая в тот же момент времени являются некоррелированными с.в. (а для нормального процесса и независимыми).
. Для дифференцируемого стационарного процесса ордината с.ф. и ее производной, взятая в тот же момент времени являются некоррелированными с.в. (а для нормального процесса и независимыми).
При умножении с.ф. на детерминированную получаем с.ф. Z(t)=a(t)X(t), корреляционная функция которой равна
KZ(t1,t2)=a(t1)a(t2) KX(t1,t2) (72.5),
где a(t) - детерминированная функция.
Сумма двух с.ф. является тоже с.ф. Z(t)=X(t)+Y(t) и ее корреляционная функция при наличии корреляционной связи между X(t) и Y(t):
KZ(t1,t2)=KX(t1,t2)+ KY(t1,t2)+2KXY(t1,t2), (73.5)
где KXY(t1,t2) - см. (68.5) - взаимная корреляционная функция двух зависимых с.ф. X(t) и Y(t).
Если X(t) и Y(t) независимы, то KXY(t1,t2)=0. М.о. с.ф. Z(t):  .
.
Метод статистических испытаний
Производится достаточно большое число статистических испытаний по схеме Бернулли, т.е. на каждом испытании генерируются случайные реализации всех исходных величин. Далее, например, если необходимо определить вероятность отказа системы, то испытания проводятся n раз, и каждый раз проверяется условие наступления отказа (например, Q>R, где Q – фактическая нагрузка на систему, R – прочность системы). Затем частота появления отказа: P*(A)=m/n, где m – количество отказов. При n®¥ -
P*(A)®P(A),
где P(A) – вероятность наступления отказа, являющаяся достоверной величиной.
В данном методе необходимо оценить погрешность определения P*(A) при определенном количестве испытаний n¹¥ или оценить количество испытаний n, необходимое для достижения частотой наступления отказа P*(A) достаточной достоверности.
ПРОСТЕЙШИЕ МОДЕЛИ НАДЕЖНОСТИ
Пример.
Дано: стальная статически определимая ферма. Нагрузка и размеры детерминированы, прочность всех стержней случайна, независима и распределена одинаково по нормальному закону. Сталь С245. Расчетное сопротивление Ry = 240 МПа, матожидание предела текучести  МПа, стандарт предела текучести s(Ry) = 20 МПа. Тогда коэффициент вариации предела текучести
МПа, стандарт предела текучести s(Ry) = 20 МПа. Тогда коэффициент вариации предела текучести
 (7,7%).
(7,7%).
Обычным путем получены усилия, подобраны сечения и найдены напряжения в стержнях фермы. Необходимо найти вероятность неразрушения (надежность) фермы.
Функция распределения прочности элементов:
 ,
,
где s - напряжение, действующее в стержне.
Значение P(s) – есть вероятность того, что случайный предел текучести Ry будет меньше действующего напряжения s, т.е. вероятность разрушения. Через интеграл вероятности Гаусса:  определим вероятности разрушения каждого стержня:
определим вероятности разрушения каждого стержня:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
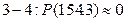 ,
,  .
.

| Элемент | Расчетное усилие, кН | Унифицированное сечение | Площадь А, см2 | Напряжение s, МПа | 
| Вероятности разрушения | |
| ВП | 3-5 | -316 | 2L100x7 | 25.6 | -220.4 | 0.0239 | |
| 5-7 | -316 | 25.6 | -220.4 | 0.0239 | |||
| НП | 1-4 | 232.2 | 2L75x5 | 14.78 | |||
| 4-6 | 313.2 | 14.78 | 0.0082 | ||||
| Ст. | 4-5 | -60.81 | 2L50x5 | 9.6 | -141 | ||
| Рас. | 1-3 | -313.8 | 2L90x6 | 21.2 | -221 | 0.0256 | |
| 3-4 | 148.2 | 2L50x5 | 9.6 | 154.3 | |||
| 4-7 | -30.7 | 2L63x5 | 12.26 | -104.4 |
Тогда по (93.8) вероятность неразрушения фермы (надежность):
1 - Pc(r) = (1-0.0239)4×(1-0.0082)2×(1-0.0256)2=0.8478.
Ферма обладает такой надежностью в случае действия максимальных нагрузок, вероятность появления которых невелика, поэтому действительная надежность фермы больше. Кроме того, ферма не является в действительности статически определимой системой и появление в стержне напряжения равного пределу текучести не есть еще разрушение этого стержня.
Литература
1. Арнольд В.И. Теория катастроф. – М.: Физматгиз, 1990.-126 с.
2. Аугусти Г., Баратта А., Кашиати Ф. Вероятностные модели в строительном проектировании. М.: Стройиздат, 1988.-584 с.
3. Барзилович Е. Ю., Беляев Ю. К. и др. Вопросы математической теории надежности. - М.: Радио и связь, 1983.-376с.
4. Барлоу Р., Прошан Ф. Математическая теория надежности и испытания на безотказность. /Пер. с англ. - М.: Советское радио, 1969.-488 с.
5. Барлоу Р., Прошан Ф. Статистическая теория надежности и испытания на безотказность. /Пер. с англ. - М.: Наука, 1984.-328с.
6. Болотин В. В. Методы теории вероятностей и теории надежности в расчетах сооружений. - 2-е изд., перераб. и доп. -М.: Стройиздат, 1981.-351 с.
7. Болотин В.В. Применение методов теории вероятностей и теории надежности в расчетах сооружений. – М.: Стройиздат, 1971.-255с.
8. Болотин В.В. Статистические методы в строительной механике. – М.: Стройиздат, 1965.-202с.
9. Вентцель Е.С. Теория вероятностей. – М.: Наука, 1989.
10. Волков С.Д. Статистическая теория прочности. – М.: Машгиз, 1960.-176 с.
11. Вопросы безопасности и прочности строительных конструкций/Сб. ст. под ред. А.Р. Ржаницына. – М.: Стройиздат, 1952.-178 с.
12. Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для вузов. Изд. 7-е, стер. – М.: Высш. школа, 1999.-479с .
13. Гнеденко Б.В. Вопросы математической теории надежности. – М.:, 1983.
14. Гнеденко Б.В., Беляев Ю.К., Соловьев А.Л. Математические методы в теории надежности. – М.: Наука, 1965.-524 с.
15. Капур К., Ламберсон Л. Надежность и проектирование систем. – М.: Мир, 1980.-604 с.
16. Кудзис А.П. Оценка надежности железобетонных конструкций. – Вильнюс: Моклас, 1985.-155 с.
17. Ломакин В.А. Статические задачи механики твердых деформируемых тел. М., «Наука», 1970.
18. Лужин О.В. Вероятностные методы расчета сооружений. – М.: МИСИ им. Куйбышева, 1983.-122 с.
19. Нагрузки и надежность строительных конструкций. Труды ЦНИИСК. Вып. 21, М., 1973.
20. Надежность и долговечность строительных конструкций [Сб. статей]. – Волгоград, 1974.
21. Проблемы надежности в строительной механике [Сб. статей]. – Вильнюс: Изд-во “Вайздас”, 1968.-302с., 1971.-208с., 1975.-215 с.
22. Проблемы надежности в строительном проектировании [Сб. статей]. – Свердловск, 1972.-296 с.
23. Райзер В.Д. Методы теории надежности в задачах нормирования расчетных параметров строительных конструкций. – М.: Стройиздат, 1986.-192 с.
24. Райзер В.Д. Расчет и нормирование надежности строительных конструкций. М.: Стройиздат, 1995.-348 с.
25. Райзер В.Д. Теория надежности в строительном проектировании:– М.: Изд-во АСВ, 1998.-304 с.
26. Ржаницын А. Р. Теория расчета строительных конструкций на надежность. -М.: Стройиздат, 1978.-239 с.
27. Саульев В.К. Статистическое моделирование: Метод Монте-Карло. – М.: МАИ, 1974.-67 с.
28. Свешников А.А. Прикладные методы теории случайных функций. – М.: Наука, 1968.-463 с.
29. Синицын А.П. Расчет конструкций на основе теории риска. – М.: Стройиздат, 1985.-304 с.
30. Тимашев С.А. Надежность больших механических систем. – М.: 1981.
31. Тихонов В.И. Выбросы случайных процессов. – М.: , 1970.
32. Хан Г., Шапиро С. Статистические модели в инженерных задачах. – М.: Мир, 1969.-396 с.
33. Руководство по расчету зданий и сооружений на действие ветра. – М.: Стройиздат, 1978
34. СНиП 2.01.07-85* Нагрузки и воздействия
ПРИЛОЖЕНИЕ
Задания по вариантам в Excel
Шумилов К. А.
Козлова Е. М.
Вероятностные методы в строительной механике
Часть 1
Учебное пособие
УДК 004.92:378 (075.8)
Рецензент: профессор Б. Г. Вагер (СПбГАСУ).
Шумилов К. А., Козлова Е. М.
Вероятностные методы в строительной механике: / учебное пособие / К. А. Шумилов; СПбГАСУ. – СПб., 2015. – с.
ISBN
Предлагаемое учебное пособие представляет собой практикум по использованию методов теории вероятностей в строительстве. Обучение предполагает наличие знаний по строительной механике. Основная задача автора – научить использовать вероятностные методы для анализа качества строительных проектов.
Предназначено для студентов технических специальностей.
Рекомендовано Редакционно-издательским советом.
ISBN © К. А. Шумилов, Козлова Е. М. 2015
© Санкт-Петербургский государственный архитектурно-строительный университет, 2015
Оглавление
1. Задачи теории вероятностей в строительстве.................................................... 3
2. Основные положения теории вероятностей....................................................... 5
3. Характеристики распределения случайных величин...................................... 10
4. Некоторые наиболее важные законы распределения..................................... 20
5. Случайные функции......................................................................................... 24
6. Приближенные методы нахождения распределения функций случайных велчин 31
7. Вероятность редких событий (появление случайного события A за время T) 32
8. Простейшие модели надежности...................................................................... 33
Литература............................................................................................................ 40
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...