
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Тема 1 Системы связи и теория информации. Источники сообщений, количество информации, энтропия. Кодирование источника
Конспект лекций
по дисциплине «Теория информации»
Тема 1 Системы связи и теория информации. Источники сообщений, количество информации, энтропия. Кодирование источника
Системы связи и теория информации
Обобщенные модели передачи и хранения информации

Типы кодирования

Обобщенная модель системы передачи информации

Исторические вехи в теории и технике кодирования
1837: Электрический телеграф и код Морзе (S. Morse).
1875: Буквопечатающий телеграф и код Бодо (E. Baudot).
1924, 1928: Работы Найквиста (H. Nyquist) и Хартли (R. Hartley) по исследованию каналов связи и скорости передачи информации.
1947-48: Фундаментальные работы К. Шеннона (C. Shannon) и В.А. Котельникова, ознаменовавшие создание теории информации.
1949-50: Первые помехоустойчивые коды: Голей, (M. Golay), Хэмминг (R. Hamming).
1952: Алгоритм Хаффмена (D. Huffman) кодирования источника.
1959-60: Коды БЧХ (R. Bose, D. Ray-Chaudhuri, A. Hochquenghem) и Рида- Соломона (I. Reed, G. Solomon).
1967: Алгоритм Витерби (A. Viterbi) декодирования сверточных кодов.
1976-78: Криптография с открытым ключом (W. Diffie, M. Hellman, R. Rivest, A. Shamir, A. Adleman and others).
1977-78: Словарные алгоритмы компрессии данных (A. Lempel, J. Ziv).
1979-1982: Модуляция на основе решетчатых кодов (G. Ungerboek).
1993: Турбо-коды (C. Berrou, A. Glavieux, P. Titimajshima).
Источники сообщений, количество информации, энтропия
1.2.1 Идея определения количества информации
С теоретической точки зрения любая универсально применимая мера количества информации в сообщении, должна опираться только на степень предсказуемости последнего. Чем менее предсказуемо (вероятно) сообщение (событие), тем большее количество информации генерируется в результате его осуществления.
Математическая модель источника информации. Дискретные и непрерывные источники
Дискретным называется источник, множество X возможных сообщений которого конечно или счетно X={x1, x2, …}. Подобный источник полностью описывается набором вероятностей сообщений: p(xi), i=1,2, … . Условие нормировки:

Рассматривая непрерывные источники, мы ограничимся только теми, несчетный ансамбль которых может быть ассоциирован с непрерывной случайной переменной, т.е. описан в терминах плотности вероятности W(x).
Условие нормировки:

Количество информации в сообщении
Аксиомы количества информации (требования к универсальной информационной мере):
1. Количество информации в сообщении x зависит только от его вероятности:

2.Неотрицательностьколичества информации:

причем I(x)=0толькодля достоверного события (p(x)=1).
3. Аддитивность количества информации для независимых сообщений:
 .
.
Единственной функцией, удовлетворяющей этим трем аксиомам оказывается логарифм вероятности сообщения:
 .
.
Единица измерения количества информации зависит от выбора основания логарифма. Традиционное основание два дает единицу измерения количества информации, называемую битом (binary digit).
Энтропия дискретного источника
Энтропия дискретного источника есть среднее количество информации в его сообщениях:
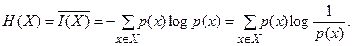
Свойства энтропии:
1.Энтропия неотрицательна:

где равенство нулю имеет место только для полностью детерминированного (неслучайного) источника.
2.Энтропия ограничена сверху соотношением
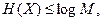
с равенством только для ансамбля M равновероятностных сообщений.
3. Энтропия ансамбля пар сообщений, генерируемых двумя независимыми источниками аддитивна:

Энтропия двоичного источника (p – вероятность одного из двух сообщений):


Кодирование источника
1.3.1 Основные определения
При кодировании источника M сообщений ансамбля источника отображаются на M кодовых слов или кодовых векторов,элементы которых принадлежат некоторому алфавиту. Код – это попросту множество всех кодовых слов. Если длины всех слов одинаковы, код называется равномерным или фиксированной длины (пример – ASCII код). Коды, в которых допускаются разные длины слов, называются неравномерными (переменной длины).

Цель кодирования источника – наиболее экономное представление сообщений, т.е. отображение их словами по возможности меньшей длины.
Код Шеннона-Фано
На первом шаге рассматриваемого алгоритма ансамбль источника разбивается на два подмножества, совокупные вероятности которых максимально близки друг к другу, т.е. к 1/2. Всем сообщениям первого из подмножеств присваивается первый символ кодового слова 0, а второго –первый символ 1. На втором шаге каждое из подмножеств вновь разбивается на два с максимально близкими совокупными вероятностями и кодовые слова первого из полученных подмножеств получают в качестве второго символа 0, а второго – 1 и т. д. Как только сообщение оказывается единственным в подмножестве, его кодирование заверено. Процедура повторяется до исчерпания всех сообщений ансамбля.
Нетрудно показать, что средняя длина кода Шеннона-Фано удовлетворяет правому неравенству Теоремы 1.3.2:

Пример 1.3.3 Закодируем дискретный источник M=8 сообщений, имеющих вероятности, перечисленные в таблице.
| X | p(x) | |||||
| x1 | 0.40 | |||||
| x2 | 0.20 | |||||
| x3 | 0.15 | |||||
| x4 | 0.10 | |||||
| x5 | 0.05 | |||||
| x6 | 0.04 | |||||
| x7 | 0.03 | |||||
| x8 | 0.03 |
В данном случае logM =3, энтропия источника H(X)»2.44 бит, асредняя длина кодового слова:

Код Хаффмена
Этот код оптимален в том смысле, что ни один префиксный код не может обладать меньшей средней длиной слова. На первом шаге кодирования по Хаффмену два наименее вероятных сообщения объединяются в одно суммарное, вероятность которого равна сумме вероятностей исходных. При этом одному из исходных сообщений присваивается кодовый символ 0, а другому – 1. На втором шаге повторяется то же самое с новым ансамблем из M-1 сообщений и вновь два наименее вероятных сообщения объединяются в одно с присвоением символа 0 одному из них и 1 – другому. Процедура повторяется M-1 раз, т. е. вплоть до шага, когда одному из двух оставшихся сообщений присваивается символ 0, а другому - 1. В результате получается кодовое дерево, чтением которого справа налево формируются кодовые слова для всех сообщений кодируемого ансамбля.
Удобнее, приступая к процедуре кодирования, записать все сообщения в порядке убывания их вероятностей. Следует также отметить, что, в противоположность алгоритму Шеннона-Фано, в ходе кодирования по Хаффмену любое кодовое слово появляется в обратном порядке.
Пример, приведенный ниже иллюстрирует процесс кодирования и демонстрирует сравнительное преимущество кода Хаффмена.
Пример 1.3.4 Закодируем по Хаффмену ансамбль из Примера 1.3.3:

Средняя длина:

Теоремы кодирования для канала
Пусть одно из M равновероятных сообщений, закодированное некоторым кодовым словом длины n, поступает на вход канала. Это означает, что мы пытаемся пропустить через канал

бит информации на каждый кодовый символ. Параметр R называется скоростью передачи или скоростью кода. Именно соотношение между скоростью R и пропускной способностью C говорит о потенциальной надежности передачи данных по каналу. Соответствующие утверждения содержатся в замечательных теоремах Шеннона:
Теорема 2.4.1 (Обратная теорема кодирования). При скорости, превышающей пропускную способность канала,R>C,не существует кода, гарантирующего произвольно малую вероятность ошибочного декодирования.
Теорема 2.4.2 (Прямая теорема кодирования). При скорости, меньшей пропускной способности канала,R<C, обязательно существует код, обеспечивающий произвольно малую вероятность ошибочного декодирования.
Первая теорема говорит о недостижимости высокой надежности передачи данных при скорости R, большей пропускной способности C. В противовес этому, если скорость R меньше емкости канала C, в принципе всегдаможно передавать данные с любой наперед заданной надежностью.
Прямая теорема Шеннона является типичной математической теоремой существования, не давая ни малейшего намека на то, как практически отыскать хотя бы один фигурирующий в ней код. Дисциплиной, посвященной поиску путей реальной утилизации потенциала, декларируемого прямой теоремой, является теория кодирования.
Дискретный канал без памяти
Как следует из определения, пропускная способность ДКБП
 ,
,
 ,
,
где использовано свойство симметрии взаимной информации. Поскольку
 ,
,
задача состоит в максимизации I(X;Y) при заданных переходных вероятностях по всем распределениям вероятности p(x), т.е. по всем векторам с неотрицательными компонентами, удовлетворяющим условию нормировки

Для модели произвольного ДКБП подобная оптимизационная задача не имеет замкнутого аналитического решения. В то же время для обширного класса симметричных каналов она, как правило, решается достаточно просто, что иллюстрируется рассматриваемым далее примером.
Существует наверняка.
Если k=logM целое число, эта граница модифицируется в более точную границу Варшамова–Гилберта, устанавливающую существование кода, удовлетворяющего неравенству:

Для больших длин n биномиальные коэффициенты в приведенных неравенствах можно аппроксимировать по Стирлингу, придя к асимптотическим версиям нижних и верхних границ, выражающим условия существования кодов в терминах скорости R и относительного кодового расстояния d/n:
Если n>>1, код не существует при нарушении любого из неравенств

(асимптотические границы Хэмминга и Плоткина),но существует наверняка при условии (асимптотическая граница Гильберта):
 ,
,
где h(·) – энтропия двоичного ансамбля.
Приведенный ниже рисунок поясняет смысл асимптотических границ.

Коды с параметрами M, n, d,попадающими в область выше любой из границХэмминга или Плоткина, существовать не могут, тогда как в области ниже границы Гилберта существование кодов гарантировано. Область между двумя упомянутыми является зоной неопределенности, для которой однозначный ответ о существовании кода нельзя получить с помощью рассмотренных границ (использование упоминавшихся более точных границ позволяет, разумеется, в той или иной мере сузить зону неопределенности).
Тема 4 Линейные блоковые коды
Введение в конечные поля
Конечным полям принадлежит основополагающая роль в теории кодирования. Начнем с общего определения алгебраической конструкции, именуемой полем.
ПолемF называется множество элементов, замкнутое относительно двух операций, называемых сложением и умножением (и обозначаемых традиционно знаками «+» и «·»). Замкнутость означает, что результаты сложения или умножения (сумма и произведение) также принадлежат F:

При этом сложение и умножения должны удовлетворять следующим аксиомам:
1. Сложение и умножение коммутативно:

2. Сложение и умножение ассоциативно:

3. В F присутствуют два нейтральных элемента – нуль (обозначаемый символом «0») и единица (обозначаемая как «1»), не меняющие операндов в сложении и умножении соответственно:

4.Для любого элемента aÎF имеется противоположный ему элемент (обозначаемый «–a»), т. е. такой, сумма a с которым равна нулю:

5. Для любого ненулевого элемента aÎF имеется обратный (обозначаемый «a–1»), т.е.такой произведение a на который равно единице:

6. Сложение и умножение подчиняются закону дистрибутивности:

Из перечисленных аксиом следует, что в любом поле наряду со сложением и умножением определены вычитание и деление:
 и для
и для 

Простейшие среди полей – числовые (рациональных или действительных чисел), содержащие бесконечно много элементов. Теория кодирования, однако, в основном оперирует с конечными полями, имеющими конечное число элементов. Общепринятое обозначение конечного поля – GF(q) (Galois field – поле Галуа, по имени французского математика XIX столетия), где q – порядокполя,т.е.число его элементов.
Можно доказать, что порядки любых конечных полей – натуральные степени простых чисел и только они: q=pm (p – простое, m – натуральное). Конечное поле простого порядка p называется простым полем. Любое простое можно сконструировать как множество остатков от деления натуральных чисел на p {0, 1, … , p–1}с операциями сложения и умножения по модулю p. Ниже даны примеры таблиц сложения и умножения в полях GF(2), GF(3), GF(5).

Операции в расширенных конечных полях (порядка q=pm, m>1), изучаемых позднее, несколько сложнее, чем сложение и умножение по модулю q.
Коды Хэмминга
Коды, фигурирующие в заголовке, замечательны как в познавательном, так и в практическом аспекте. Выпишем все различные ненулевые m–разрядные двоичные числа (m–компонентные векторы) как столбцы в некотором, скажем натуральном (возрастающем) порядке и используем полученную матрицу в качестве проверочной для линейного кода. Подобная матрица имеет размер m´(2m–1). Полученный код и есть код Хэмминга длины n= 2m–1. Так как число строк проверочной матрицы равно числу проверочных символов, код Хэмминга имеет k=n–m=2m–m–1 информационных символов, т.е. является (2m–1, 2m–m–1) линейным кодом.
Пример 4.5.1 Столбцы проверочной матрицы двоичного кода Хэмминга (7,4) есть десятичные числа от 1 до 7, в двоичной записи.
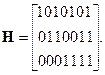
Если нужен систематический код Хэмминга, достаточно переупорядочить столбцы проверочной матрицы H, выделив явно m´m единичную матрицу как составной блок проверочной. После этого легко строится и каноническая порождающая матрица.

Так как все столбцы матрицы H кода Хэмминга различны, любая их пара линейно независима, в то время как сумма пары любых столбцов является каким-то третьим столбцом H. Поэтому в силу теоремы 6.4.1 расстояние кода Хэмминга равно трем и такой код исправляет любую однократную ошибку.
Коды Хэмминга являются почти уникальным примером совершенных двоичных кодов. Известны и недвоичные коды Хэмминга.
В таблице приведены параметры нескольких кодов Хэмминга в порядке возрастания длин.

Расширенные и укороченные коды
Любой линейный (n,k) код U можно превратить в код U´ с параметрами (n+1, k) добавлением символа общей проверки на четность. Пусть, например, u=(u1, u2, … , un) – произвольное кодовое слово исходного (n,k) линейного кода U. Тогда соответствующее слово расширенного кода U´ строится по правилу u´=(u1, u2, … , un, un+1) , где un+1= u1+ u2+ … + un (разумеется с суммированием согласно двоичной арифметике, т.е. по модулю 2). В итоге

и, следовательно, вес любого слова в расширенном коде будет четным. Это, в свою очередь, означает, что при нечетном расстоянии d исходного кода U минимальное расстояние d´ расширенного кода U´ увеличится на единицу: d´ = d+1. Тем самым, любой линейный (n,k) код нечетного расстояния d, исправляющий t=(d–1)/2 ошибок, можно трансформировать в расширенный (n+1, k) код, исправляющий ошибки прежней кратности t=(d–1)/2=(d´/2)–1 и, вдобавок, обнаруживающий ошибки кратности t+1. Порождающая матрица G´ расширенного кода получается из исходной G добавлением общих проверок на четность строк последней.
Коды Хэмминга весьма наглядны в части иллюстрации сказанного. Так как расстояние любого такого кода равно трем, в результате расширения получается (2m, 2m–m–1) код с расстоянием четыре, который, в дополнение к исправлению любых однократных, обнаруживает и любые двукратные ошибки. Поучительный пример реального применения расширенного (32,26) кода Хэмминга для передачи цифрового потока данных с искусственного спутника Земли дает глобальная радионавигационная система космического базирования GPS.
Другой популярный прием преобразования имеющихся кодов в новые – укорочение. Укороченный код получается из исходного систематического отбором лишь слов, имеющих l первых нулевых символов. Зная наперед об этом свойстве всех отобранных слов, нет нужды передавать упомянутые нулевые символы, уменьшив длину кода на l с одновременным сокращением на ту же величину числа информационных бит. Результирующий (n–l, k–l) код будет обладать расстоянием, не худшим, чем у исходного. Легко показать, что порождающая матрица G´ укороченного кода получается из канонической матрицы G исходного удалением первых l строк и столбцов.
Пример 4.6.1Удалив в канонической порождающей матрице (7,4) кода Хэмминга два левых столбца и две верхних строки, придем к канонической порождающей матрице укороченного линейного (5,2) кода
 .
.
Разумеется, этот код – подобно исходному коду Хэмминга – исправляет любую однократную ошибку.
Тема 5 Циклические коды
Циклические кодеры
Линейность циклических кодов означает безоговорочную применимость к ним всех методов кодирования и декодирования, рассмотренных в предыдущей главе. В то же время свойство цикличности зачастую открывает дополнительные возможности упрощения кодера в аппаратной реализации. Так, если приемлем несистематический вариант кода, структура кодера оказывается особенно простой. Поскольку любой кодовый полином u(z) такого кода есть произведение информационного a(z) и порождающего g(z) полиномов, компоненты соответствующего кодового вектора uявляются сверткой информационной последовательности a0, a1, … , ak–1 с последовательностью коэффициентов порождающего полинома g0, g1, … , gn–1.
Подобная операция реализуется фильтром с конечной импульсной характеристикой (КИХ–фильтром) вида

Обратимся теперь к структуре систематического циклического кодера. Согласно сказанному в параграфе 7.3, ключевой операцией в построении систематического кодового полинома циклического кода является нахождение остатка r(z) от деления произведения zn–ka(z) на порождающий полином g(z). Чтобы понять, каким образом структура, представленная далее, вычисляет r(z), разделим zn–ka(z)=ak–1zn–1+ak–2zn–2+…+a0zn–k на g(z)=zr+gr–1zr–1+ +…+g0, используя правило длинного деления. На первой итерации g(z) умножается на ak–1zn–r–1 и результат вычитается из делимого.

В итоге первый остаток r1(z)=r1,n–2zn–2+r1,n–3zn–3+…+r1,n–r–1zn–r–1 имеет степень не более n–1 и после сложения с ak–2zn–2 используется на второй итерации как новое делимое. При выполнении второй итерации из него вычитается (r1,n–2+ak–2)zn–r–2g(z) , давая второй остаток r2(z)=r2,n–3zn–3+r2,n–4zn–4+…+r2,n–r–2zn–r–2, степень которого не превышает n–3. Остаток r2(z) вновь суммируется с ak–3zn–3 и используется как делимое на третьей итерации и т.д. Легко видеть, что на i-й итерации предыдущий остаток, сложенный с
an–izn–i, служит делимым, из которого вычитается произведение полинома g(z) на z в степени, уравнивающей степени вычитаемого и делимого, а также на коэффициент, равный старшему коэффициенту делимого. Результатом этого оказывается очередной остаток, с которым производятся те же действия на следующей итерации. После k итераций k-й остаток имеет степень, меньшую r, являясь, очевидно, требуемым остатком r(z). Подобное «длинное деление» реализуется систематическим циклическим кодером, показанным на предыдущем слайде и основанным на регистре сдвига с линейной обратной связью.

Исходно ключ S1 замкнут, а ключ S2 находится в положении 1. Биты данных подаются на вход, начиная со старшего ak–1. Допустим, что в r ячейках регистра сдвига записаны коэффициенты текущего делимого. Тогда в точке B присутствует старший коэффициент текущего делимого, а в точках C0 … Cr–1 – его произведения с коэффициентами порождающего полинома. Следовательно, в точках B1…Br–1 формируются коэффициенты разности текущего делимого и порождающего полинома, умноженного на старший коэффициент делимого и соответствующую степень z,т.е. коэффициенты следующего остатка. При подаче тактового импульса эти коэффициенты записываются в ячейки регистра, подготавливая его к новой итерации. После k итераций регистр содержит остаток r(z), и, чтобы передать последний на выход, ключ S1 размыкается, а S2 переводится в положение 2. В результате на выходе после бита данных a0 следует старший коэффициент r(z) (первый проверочный символ), и т.д.
Пример 5.5.1 Кодер (7,4) кода из примера 5.3.2 приведен на следующем слайде. Там же дана таблица, содержащая значения информационных битов, состояние регистра и выходное слово. Как видно, при прежнем информационном полиноме a(z)=z2+z+1 последняя колонка таблицы, читаемая снизу вверх, совпадает со словом, полученным в примере 5.3.2.

Расширенные конечные поля
Как уже известно, конечные поля существуют только для порядков q=pm (p – простое, m – натуральное). Простое поле порядка p, GF(p), можно трактовать как множество {0, 1, …, p–1} остатков от деления целых чисел на p с операциями сложения и умножения по модулю p. Подобно этому расширенное поле GF(pm) порядка q=pm при m>1 можно ассоциировать с множеством остатков от деления полиномов над GF(p) на некоторый неприводимый полином f(x) степени m с операциями сложения и умножения по модулю f(x). Другими словами, поле GF(pm) можно представить всеми полиномами над простым полем GF(p) степени не выше m–1 с обычным полиномиальным сложением. Умножение же в нем выполняется в два шага – сперва как обычное умножение полиномов, но с удержанием в качестве конечного итога лишь остатка от деления полученного произведения на неприводимый полином f(x).
Пример 5.7.1 Обратимся к полиному f(x)=x3+x+1. Поскольку он неприводим и имеет степень deg(f(x))=3, его можно использовать для построения расширенного поля GF(23)=GF(8). Возьмем два полинома степени не выше двух, например, a(x)=x2+x+1 и b(x)=x+1. Их сумма в поле GF(8) a(x)+b(x)= x2+x+1+x+1= x2. Чтобы найти их произведение в GF(8), вначале перемножим их обычным образом, придя к (x2+x+1)(x+1)= =x3+x2+x2+x+x+1=x3+1, после чего разделим полученный результат на f(x) с последующим удержанием только остатка: x3+1=q(x)f(x)+r(x)=1·(x3+x+1)+x. Таким образом, по правилам умножения в GF(8) a(x)b(x)=(x2+x+1)(x+1)=x. Поскольку сложение в расширенном поле выполняется без каких-либо затруднений (сложение коэффициентов полиномов), ниже приводится лишь полная таблица умножения, построенная на основе неприводимого полинома f(x)=x3+x+1.

Отметим, что в числе полиномов степени не выше m–1 присутствуют и полиномы нулевой степени, т.е. элементы простого поля GF(p) , сложение и умножение которых, осуществляются по правилам GF(p). Это означает, что простое поле GF(p) полностью содержится в расширенном GF(pm) , или, другими словами, GF(p) является подполем GF(pm). Порядок простого подполя GF(p) поля GF(pm) называется характеристикой GF(pm). Этот параметр проявляет себя, например, при вычислении сумм и произведений элементов GF(pm), так как коэффициенты представляющих элементы поля полиномов находятся на основе арифметики по модулю p. Любое расширенное поле GF(2m) является полем характеристики 2, вследствие чего при вычислении коэффициентов полиномов, представляющих элементы GF(2m), используется арифметика по модулю два. В частности, для любого aÎGF(2m) –a=a , поскольку a+a=0.
Двоичные коды БЧХ
Накопленные к данному моменту знания открывают путь к ознакомлению с одним из наиболее замечательных классов блоковых кодов. Конструкция БЧХ дает один из редких примеров построения кодов с предсказуемыми и варьируемыми в широком диапазоне корректирующими свойствами. Коды, описываемые ниже, являются примитивными, входящими как частный (хотя и наиболее важный) подкласс в общее семейство БЧХ-кодов. Они имеют длину n=2m–1 и строятся на основе расширенного поля GF(2m). Обобщение теории БЧХ-кодов на p-ичный (p>2) алфавит не вызывает затруднений, однако недвоичные БЧХ-коды, за исключением кодов Рида-Соломона не столь привлекательны с точки зрения приложений. Принцип построения БЧХ-кодов декларируется следующим утверждением
Теорема 5.8.1 (теорема БЧХ). Пусть полином g(z) имеет в расширенном поле GF(2m) корни V, V2, …, Vs , где V – примитивный элемент поля GF(2m).Тогда циклический код с порождающим полиномом g(z) имеет минимальное расстояние d, не меньшее s+1.
Для доказательства теоремы предположим, что имеется кодовое слово веса s или менее. Делимость его кодового полинома u(z) на порождающий g(z) означает обращение этого полинома в нуль при z=Vi, i=1,2, …, s:
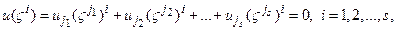
где j1, j2, …, js обозначают позиции компонентов слова, которые могут быть ненулевыми. Как видно, существование кодового слова веса s или менее равносильно существованию ненулевого решения квадратной s´s системы линейных уравнений с нулевой правой частью. Подобное решение существует только при вырожденной матрице системы. Матрица же нашей системы (ассоциированная с известной матрицей Вандермонда) имеет специфический вид

и не может быть вырожденной, если все элементы первой строки различны. Но последнее имеет место всегда, так как ς - примитивныйэлемент и 2m–1> >j1>j2>…>js³0.
Теперь алгоритм построения БЧХ-кодов можно описать следующим образом. Для значения m, обеспечивающего необходимую длину кода n=2m–1, выбирается примитивный полином f(x) и строится расширенное поле GF(2m), как это сделано в примере 5.7.6. После этого в поле GF(2m) выбираются степени примитивного элемента
V, V2, …, Vs, которым предстоитслужить корнями порождающего полинома. Любой из них, однако, должен войти в число корней порождающего полинома только вместе со всеми своими сопряженными. Таким образом, вместе с элементом V придется взять и элементы V2, V4, … , придя тем самым к сомножителю порождающего полинома g(z) согласно теореме 5.7.5:
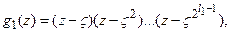
где l1 – длина сопряженного цикла элемента V, равная m вследствие примитивности V. Полином g1(z) – является двоичным полиномом минимальной степени, имеющим корень V, т.е. минимальным полиномом V. Следующим корнем порождающего полинома должен быть элемент V2, уже учтенный сомножителем g1(z), так как он сопряжен с V. Если s>2, следующим корнем порождающего полинома должен быть элемент V3 также со всеми своими сопряженными (V3)2, (V3)4, … , что означает включение в g(z) сомножителя в виде минимального полинома элемента V3

где l3 – длина сопряженного цикла для V3. Подобные шаги продолжаются пока не будут найдены минимальные полиномы для всех элементов множества V, V2, …, Vs,не охваченных ранее. По исчерпании всех необходимых корней порождающего полинома g(z) последний строится как произведение всех найденных минимальных полиномов:

Гарантией того, что построенный таким образом полином можно использовать как порождающий для циклического кода, служит делимость на него бинома zn–1, где
n=2m–1 (см. теорему 5.2.2). В самом деле, полином g(z) является произведением некоторых биномов вида z–a с различными ненулевыми элементами aÎGF(2m), тогда как в силу теоремы 5.7.6 бином zn–1 есть произведение всех подобных биномов.
Пример 5.8.1 Построим порождающий полином g(z) БЧХ-кода длины n=23–1=7, исправляющего любую однократную ошибку. Необходимое для этого расширенное поле GF(8) уже построено в примере 5.7.6. Поскольку s=2t=2, корнями порождающего полинома должны быть элементы V и V2. Минимальный полином элемента V имеет вид g1(z)=(z+V)(z+V2)(z+V4)= =z3+(V+V2+V4)z2+(VV2+VV4+V2V4)z+VV2V4. Но V+V2+V4=V+V2+V+V2=0, VV2+VV4+V2V4= =V3+V5+V6=V+1+V2+V+1+V2+1=1, VV2V4=V7=1, так что g1(z)= z3+z+1. Элемент V2, уже учтен в g1(z), а других обязательных корней g(z) нет, поэтому g(z)= =g1(z)=z3+z+1. Поскольку deg(g(z))=3, число информационных символов кода k=4, и, таким образом, построенный код оказался циклической версией (7,4) кода Хэмминга, исправляющего любую однократную ошибку.
Если изменить условия примера, потребовав исправления до двух ошибок (t=2Þs=4), множество обязательных корней полинома g(z) пришлось бы расширить до V, V2, V3, V4. Поскольку элементы V, V2 and V4 входят в один и тот же сопряженный цикл, т.е. уже охвачены минимальным полиномом g1(z), остается найти лишь минимальный полином для V3 (корнями которого будут и сопряженные с ним элементы V6 и V12= V5). Степень последнего равна трем, так что степень g(z) окажется равной шести, и полученный код есть тривиальный (7,1) код с повторением, передающий лишь один бит информации.
Разумеется, в наши дни системный дизайнер свободен от необходимости поиска порождающих полиномов БЧХ-кодов, поскольку подобная работа давно проведена, и детальные таблицы готовых к употреблению полиномов можно найти во многих источниках. Однако любой инженер или аналитик, причастный к канальному кодированию, должен уметь быстро оценивать параметры БЧХ-кодов. Грубую нижнюю границу числа информационных символов БЧХ-кода легко вывести, учтя, что любая четная степень V2i примитивного элемента V входит в сопряженный цикл элемента меньшей степени Vi и, следовательно, охвачена некоторым уже построенным минимальным полиномом. Как результат, общее количество сопряженных циклов для всех обязательных корней порождающего полинома не больше s/2=t (при s=2t), а так как длина любо
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...