Исправляющая способность кода. Ключевые параметры блоковых кодов

Говорят, что код исправляетвплоть доtошибок, если при искажении любыхtили менее символов в любом его кодовом слове, последнее, тем не менее, декодируется(по минимуму расстояния)верно.

Наименьшее хэммингово расстояние между парами слов в коде называется его минимальным расстоянием(или просторасстоянием)

Теорема 3.4.1 Код исправляет вплоть доt ошибоктогда и только тогда, когда его расстояние удовлетворяет неравенству

Поучительна геометрическая интерпретация этого факта. Хэммингова сфера радиуса t с центром в u_i есть множество точек (векторов), расположенных в пределах хэммингова расстояния t от вектора u_i. Есливсе кодовые векторы удается окружить подобными сферами радиуса t без пересечений между ними, декодер сможет декодировать любой вектор в i-й сфере в i-е кодовое слово. Тем самым любая ошибка кратности t или менее в любом кодовом слове будет исправлена. Но избежать пересечения сфер радиуса t можно лишь при условии, что расстояние между любыми кодовыми векторами не меньше 2t+1.

Нетрудно также убедиться, что для обнаружения ошибок кратности вплоть до t необходимо и достаточно соблюдения условия

Длина кода n вместе с объемом M и расстоянием d составляют тройку ключевых параметров блокового. Вместо объема M можно, разумеется, использовать либо число информационных символов k=logM, либо скорость кода R=k/n. Понятно, что поиск кодов, имеющих высокие показатели в отношении обнаружения и исправления ошибок, сводится к максимизации расстояния d при заданных M (k или R) и n. Дуальной задачей является максимизация скорости R=k/n (эквивалентно k или M) при заданных расстоянии d и длине n.

Важнейшие границы теории кодирования

Очевидно, особый интерес представляют коды с максимальным расстоянием при заданных длине и объеме (или с максимальной скоростью при заданных длине и расстоянии). Что же в этом плане может быть достигнуто в принципе? Отчасти на этот вопрос отвечают фундаментальные границы теории кодирования. Начнем с границы Хэмминга.

Теорема 3.5.1(Граница Хэмминга). Любой двоичный код, исправляющий вплоть доtошибок, удовлетворяет неравенству:

Коды, лежащие на границе Хэмминга (удовлетворяющие ей с равенством), называются совершенными. Совершенные коды исправляют любые ошибки кратности t и менее, но не исправляют и не обнаруживают никаких ошибок большей кратности.

Геометрически такие коды реализуют так называемую «плотную упаковку», при которой все 2ⁿ двоичных векторов распределены по M сферам радиуса t, не имеющих пересечений и промежутков. Они названы совершенными, так как обеспечивают максимальную скорость R, допускаемую фиксированными d=2t+1 и n. Среди двоичных существуют лишь три класса совершенных кодов – тривиальный код с повторением нечетной длины, коды Хэмминга, исправляющие однократные ошибки, и код Голея длины 23 с расстоянием 7 (исправляющий ошибки вплоть до трехкратных).

Близкое по смыслу ограничение устанавливается границей Плоткина.

Теорема 3.5.2 (Граница Плоткина). Любой двоичный блоковый код подчиняется неравенству:

Обе границы декларируют необходимые (но не достаточные) условия существования кодов. Их невыполнение свидетельствует о несуществовании кода с предполагаемыми значениями M, n и d, и поэтому их можно назвать верхними. Известны и более точные (однако и более сложные) верхние границы во всем диапазоне M, n, d (Элайеса и пр.).

С другой стороны, имеются и нижние границы, устанавливающие достаточные условия существования кодов с заданными M, n, d .

Теорема 3.5.3 (Граница Гилберта). Двоичный блоковый код, параметры которого удовлетворяют неравенству

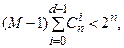
Существует наверняка.

Если k=logM целое число, эта граница модифицируется в более точную границу Варшамова–Гилберта, устанавливающую существование кода, удовлетворяющего неравенству:

Для больших длин n биномиальные коэффициенты в приведенных неравенствах можно аппроксимировать по Стирлингу, придя к асимптотическим версиям нижних и верхних границ, выражающим условия существования кодов в терминах скорости R и относительного кодового расстояния d/n:

Если n>>1, код не существует при нарушении любого из неравенств

(асимптотические границы Хэмминга и Плоткина),но существует наверняка при условии (асимптотическая граница Гильберта):

,

где h(·) – энтропия двоичного ансамбля.

Приведенный ниже рисунок поясняет смысл асимптотических границ.

Коды с параметрами M, n, d,попадающими в область выше любой из границХэмминга или Плоткина, существовать не могут, тогда как в области ниже границы Гилберта существование кодов гарантировано. Область между двумя упомянутыми является зоной неопределенности, для которой однозначный ответ о существовании кода нельзя получить с помощью рассмотренных границ (использование упоминавшихся более точных границ позволяет, разумеется, в той или иной мере сузить зону неопределенности).