Передаточная функция сверточного кода

Изучая решетчатую диаграмму, нетрудно установить, что при отыскании минимального расстояния (минимального веса) сверточного кода следует учитывать лишь пути, ответвляющиеся в некоторой точке от нулевого, а затем вновь сливающиеся с ним без последующих ответвлений. Поскольку движение вдоль нулевого пути веса не увеличивает, можно игнорировать все ветви, соединяющие нулевой узел с самим собой. Имея это в виду, найдем минимальный из весов на множестве путей, отходящих от нулевого в начале диаграммы и сливающихся с ним после некоторого числа шагов.

Пометим каждую ветвь диаграммы состояний формальной переменной D, в степени, равной весу ветви. Так, в примере 9.2.1 ветви между состояниями 00 и 10, имеющей вес два (кодовые символы 11), приписана метка D², ветви из состояния 10 в 01 (01) – метка D, ветви из 01 в 10 (00) – метка D⁰=1 и т.д. Маркированная таким образом диаграмма состояний показана ниже, где ветвь из состояния 00 в себя, согласно сказанному ранее, отброшена, а состояние 00 расщеплено на два: начальное (отвечающее ответвлению от нулевого пути) и конечное (соответствующее слиянию с нулевым путем).

Если теперь, двигаясь по некоторому пути, перемножить метки всех его ветвей, конечный показатель степени D в точности совпадет с весом пути. Если в какой-то узел диаграммы входят два пути, имеющие веса w и v, формальная сумма D^w+D^v отразит это событие без риска неоднозначности.

Так как движение по ветвям диаграммы есть рекуррентный, пошаговый процесс, вес пути на данном шаге можно выразить как сумму веса, аккумулированного на предыдущих шагах, и веса последней ветви. Обозначив веса путей, приводящих в текущие состояния 10, 01 и 11 через Y, Z, U соответственно, а итоговый вес пути в точке слияния через X, мы также можем положить начальный вес в точке ответвления равным нулю (D⁰=1) . При этом справедлива система линейных уравнений

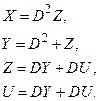
Решая систему (например, по правилу Крамера), получим

Функцию T(D) называют передаточной функцией сверточного кода. Фактически она содержит сведения о весах всех ненулевых путей решетчатой диаграммы, стартующих с нулевого состояния. После деления по схеме 1/(1–x)=1+x+x²+… , T(D) преобразуется к форме

показывающей, что рассматриваемый код имеет свободное расстояние d_f=5: из нулевого состояния выходит единственный путь веса пять, два пути веса шесть и т.д. Действуя в том же духе, передаточную функцию можно модернизировать так, чтобы для любого пути учесть также число единиц входного потока и длину. Усовершенствование состоит в маркировке ветвей диаграммы состояний добавочными формальными переменными N с показателем, равным значению входного информационного бита, и L, степень которой всегда равна единице. При этом диаграмма состояний примет вид, показанный ниже.

Теперь можно составить и решить систему уравнений, придя к передаточной функции T(D,N,L), в которой степени переменных D, N, L равны соответственно весу, числу единиц в кодируемом потоке и длине пути на решетчатой диаграмме. Для нашего примера

откуда видно, что в рассматриваемом коде присутствуют один путь длины 3 и веса 5, кодирующий блок с одним ненулевым битом, путь длиной 4 веса 6, кодирующий последовательность с двумя ненулевыми битами и т.п.

Понятно, что для более сложных кодов, чем взятый для примера, попытка нахождения передаточной функции вручную может обернуться громоздкими и утомительными расчетами, однако решение подобной задачи с помощью компьютера большого труда не составляет. В том случае, когда надобность в знании длины пути и числа ненулевых кодируемых битов отсутствует, передаточную функцию в исходной форме T(D) легко найти из T(D,N,L) подстановкой N=1, L=1.

Алгоритм декодирования Витерби

Рекурсивная природа сверточного кодирования лежит в основе также рекурсивного и ресурсно-экономного алгоритма декодирования Витерби. Подчеркнем сразу, что алгоритм Витерби оптимален, реализуя стратегию максимального правдоподобия, т.е. отыскания кодового слова, ближайшего к наблюдению, а его особое название связано лишь с элегантным способом решения этой задачи. Начнем с реализации алгоритма в жестком варианте, т.е. для ДСК, когда наблюдение y декодируется в кодовое слово, ближайшее к нему в смысле расстояния Хэмминга. Общая идея декодирования по Витерби состоит в пошаговом сравнении всех путей на решетчатой диаграмме (которые и есть кодовые слова) с наблюдением y и отбрасывании тех из них, которые заведомо окажутся дальше от y, чем некоторые другие. Если два пути, входящих в один узел, имеют вплоть до него разные расстояния от наблюдения, то у пути с бóльшим расстоянием нет шанса впоследствии оказаться ближайшим к наблюдению, поскольку при любом общем продолжении обоих путей он останется более удаленным от y, чем другой. Поэтому из двух входящих путей более удаленный от наблюдения можно исключить из дальнейшего поиска ближайшего пути. Более подробно ход декодирования можно описать следующим образом.

Назовем i-м шагом декодирования временной интервал, на котором принимается i-я n-символьная кодовая группа наблюдения y. Непосредственно перед этим моментом все пути (т.е. кодовые слова) проходят через 2^m–1 узлов (состояний) решетчатой диаграммы. На i-м шаге:

1. Вычисляются хэмминговы расстояния от принятой n-символьной группы до каждой из ветвей решетчатой диаграммы. Так как из каждого из2^m–1 узлов (состояний) выходят две ветви, всего нужно найти 2^m расстояний.

2.Исследуются пары ветвей, входящие в каждый из 2^m–1 узлов из разных предшествующих состояний:

2.1. Их расстояния Хэмминга прибавляются к накопленным до i-го шага хэмминговым расстояниям двух соответствующих путей для обновления накопленных расстояний, называемых метриками.

2.2. Метрики двух конкурирующих путей, входящих в один и тот же узел, сравниваются между собой и путь, более удаленный от наблюдения, отбрасывается и не участвует в дальнейшем декодировании. Удерживаемый путь называется выжившим.

3. Все 2^m–1 выживших путей (один на узел) сохраняются в памяти вместе с их метриками, после чего декодер готов к (i+1)-му шагу процедуры.

Как видно, ресурсосберегающий характер алгоритма связан с отбраковкой на каждом шаге ровно половины из 2^m возможных путей, входящих в 2^m–1 узлов решетчатой диаграммы. В итоге число выживших путей остается постоянным и равным общему числу состояний 2^m–1, хотя число конкурирующих кодовых слов удваивается на каждом шаге декодирования. Чтобы лучше понять, почему и как работает алгоритм Витерби, исследуем его детали на конкретном примере

Пример 6.4.1 Обратимся вновь к коду примера 6.1.1. Предположим, что наблюдение y=(100100000000000000000000).

Первые два шага декодирования тривиальны. На первом из них две ветви, стартующие из состояния 00, прибывают в состояние 00 с метрикой 1 и в состояние 10 также с метрикой 1.

На втором шаге метрика узла 00, становится равной двум, так как единственный входящий в него путь стартует из того же состояния 00, имеющего метрику 1, и это значение увеличивается на единицу, поскольку расстояние между ветвью 00®00 и текущей 2-х символьной группой y (текущая группа – на данном шаге 01 – подчеркнута на всех диаграммах) также равно 1. Подобным же образом метрика, например, узла 11, равна 3, так как прибывающий в него путь стартует из узла 10 с метрикой 1, к которой далее прибавляется два: расстояние текущей 2-группы y от ветви 10→11.

Третий шаг нашего примера критически важен в объяснении всего алгоритма. Возьмем состояние 00. Приход в него возможен двумя путями: из состояний 00 или 01. Накопленная метрика первого равна двум, поскольку он начинается из состояния 00 с метрикой 2, а расстояние Хэмминга между ветвью 00®00 и текущей 2-группой y (00) равно нулю. С другой стороны, путь из состояния 01, имеет аккумулированную метрику 3, так как метрика предшествующего состояния 01 равнялась единице, а расстояние Хэмминга ветви 01®00 от наблюдения (00) равно двум. При общем продолжении обоих путей их накопленные метрики возрастут одинаково, так что второй останется на большем расстоянии от наблюдения, чем первый. Однако декодирование по минимуму расстояния означает поиск кодового слова, ближайшего к наблюдению, а значит, путь, который заведомо останется более удаленным от y, чем некоторый другой, можно сразу отбросить. Поэтому мы вправе исключить из анализа путь, проходящий на предыдущем шаге через узел 01 (перечеркнут на рисунке), сохранив лишь путь из состояния 00, являющийся выжившимдля узла 00 на данном шаге. Подобным же образом мы исследуем состояние 10 и видим, что для него выжившим является путь через узел 01, тогда как путь через узел 00 отбрасывается как более удаленный от наблюдения y и т.д.

Следующие два шага не имеют принципиальных отличий от рассмотренного.

Придерживаясь этой стратегии, допустим, что выжили пути, показанные на предыдущем рисунке. На восьмом шаге в узле 10 возникает аналогичная двузначность. Более интересно, однако, что оба пути, прошедшие на предыдущем этапе через узел 11, выбывают из числа выживших. Понятно, таким образом, что случайный выбор пути в узле 11 предыдущего шага не имеет последствий, поскольку любой из конкурирующих путей все равно был бы исключен из дальнейшего анализа. Сценарии этого типа встречаются и на последующих девятом и десятом шагах.

В частности, чтобы устранить двузначность в узлах 10, 01 и 11 шага 9, как и ранее, бросается монета. Однако, уже на шаге 10 спорность этого выбора для узлов 01 и 11 утрачивает свое значение, так как ни один из путей через эти узлы все равно бы не выжил.

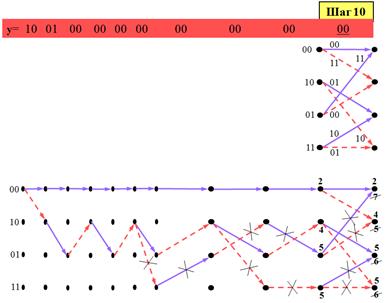
На шаге 11 имеет место ситуация, которую следует обсудить особо. Во-первых, ни один из путей, для которых ранее приходилось разрешать неоднозначность, не выжил, а значит, какие-либо последствия сомнительного выбора выживших путей на предыдущих шагах полностью исключены. Во-вторых, все выжившие пути слились с нулевым вплоть до шага 9. Это значит, что все будущие выжившие пути будут иметь общий начальный сегмент от первого до, по крайней мере, девятого шага, и, следовательно, первые девять битов можно выдать как декодированные в соответствии с информационными битами этого общего сегмента: 000000000. Шаг 12 подобным же образом оставляет среди выживших только пути с общим (нулевым) сегментом, удлиненным еще на один шаг, что позволяет декодировать очередной (десятый) бит: 0000000000.

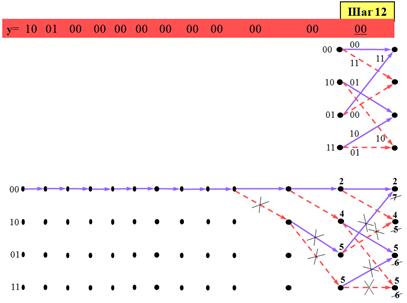
Посмотрим теперь, что происходит после того, как поток передаваемых битов заканчивается. Пусть длина битового потока равна 12. По прекращении битового потока кодер продолжает работу, поскольку для его обнуления потребуются m–1 дополнительных тактов. Можно считать, что в это время на вход кодера поступают m–1 «хвостовых» нулевых битов, предназначенных для «очитки» регистра, о чем декодер априори осведомлен. Так как, однако, генерируемые кодером символы сохраняют зависимость от предшествующих битов, их передача имеет смысл. Для рассматриваемого примера m–1=2 и символы наблюдения, отвечающие хвостовым обнуляющим битам, обесцвечены на рисунке предыдущего слайда. Поскольку декодеру известно, что, начиная с 13-го шага, производится обнуление кодера, возможны лишь переходы в состояния 00 или 01. Тем самым исключаются из рассмотрения четыре из восьми ветвей на решетчатой диаграмме, и метрики необходимо вычислять лишь для двух узлов. В результате выживают всего два пути и декодируется очередной (11-й) бит: 00000000000.

На финальном, 14-м шаге осуществляется выбор между двумя путями, сходящимися в состоянии 00, что завершает декодирование: 000000000000.

Как теперь выясняется, единственным выжившим (а значит, декодированным) путем оказался нулевой. Если нулевое кодовое слово было передано в действительности, значит произошло исправление двукратной ошибки в полном соответствии с корректирующей способностью кода (свободное расстояние d=5).

С позиций практики выдача декодированных битов по мере формирования общего сегмента всех выживших путей, вряд ли удобна. Вследствие этого нередко прибегают к усечению длины пути и принудительной выдаче декодированных битов вплоть до шага, опережающего текущий на фиксированный интервал t_d. Как показали многочисленные натурные эксперименты и компьютерные тесты, при выборе t_d порядка пяти длин кодового ограничения вероятность расхождения выживших путей до момента, опережающего текущий шаг на отрезок t_d, столь мала, что практически не нарушает оптимальности декодирования. Рассмотренный пример в некотором смысле служит тому подтверждением.