Основные свойства неопределенного интеграла

1. Производная неопределенного интеграла равна подынтегральной функции

2. Дифференциал неопределенного интеграла равен подынтегральному выражению

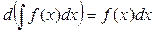
3. Неопределенный интеграл дифференциала функции равен самой функции с точностью до произвольной постоянной

4. Постоянный множитель можно выносить из под знака интеграла

5. Интеграл суммы двух функций равен сумме интегралов от этих функций.

6. Если

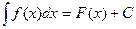
и х=φ(u) - некоторая функция, имеющая непрерывную производную, то

· При вычислении интегралов полезно знать таблицу основных дифференциалов функции

Таблица основных дифференциалов функции

df(x) = f¢(x)dx	f¢(x)dx = df(x)

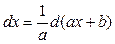
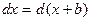
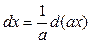
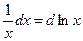
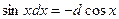
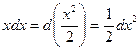
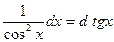
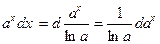
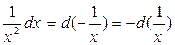
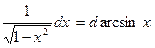
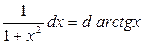
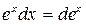
Таблица основных интегралов

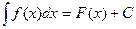
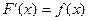
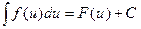
1.
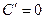
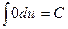
2.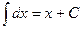
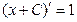
3.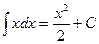
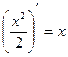
4.
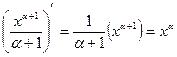
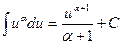
5.
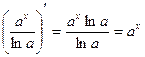
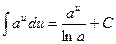
6.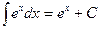
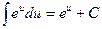
7.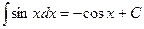
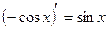
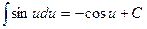
8.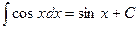
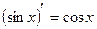
9.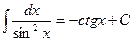
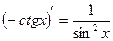
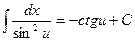
10.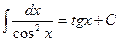
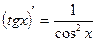
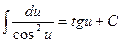
11.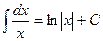
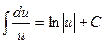
12.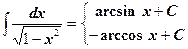
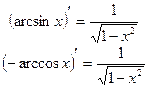
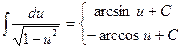
13.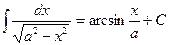
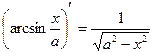
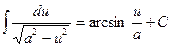
14.
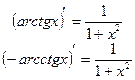
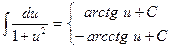
15.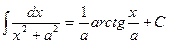
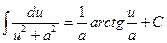
16.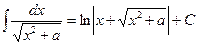
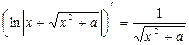
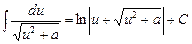
17.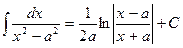

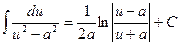
Справедливость формул интегрирования, а также и каждый результат интегрирования можно проверить путем дифференцирования, т.к. интегрирование есть действие, обратное дифференцированию.

Основные методы интегрирования

Непосредственное интегрирование

Непосредственное интегрированиезаключается в вычислении интегралов путем некоторых тождественных преобразований подынтегрального выражения и непосредственного применения таблицы основных интегралов и свойств интегралов.

Метод замены переменной

Пусть требуется вычислить интеграл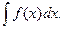

Предположим, что непосредственным интегрированием первообразную подобрать невозможно, тогда сделаем замену переменной в подынтегральном выражении x= j(t),

где j(t) - непрерывная функция с непрерывной производной, имеющая обратную функцию, и вычисление данного интеграла сведем к вычислению другого , более простого интеграла по переменной t:

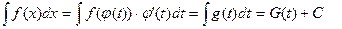
Здесь подразумевается, что после интегрирования в правой части равенства вместо t будет подставлено выражение через х на основании равенства

x = j(t).

По определению дифференциала функции выражение j^¢(х)dx можно заменить dj(х), т.к. j^¢(х)dx = dj(х). Использование данных преобразований называют “подведением под знак дифференциала”.

Интегрирование по частям

При интегрировании по частям используют формулу

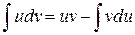
Эта формула интегрирования по частям чаще всего применяется к интегрированию выражений, которые можно так представить в виде произведения двух множителей u и dv, чтобы отыскание функции v по ее дифференциалу dv и вычисление интеграла ∫vdu составляли в совокупности задачу более простую, чем непосредственное вычисление интеграла ∫udv.

Обычно за u выбирается функция, которая при дифференцировании упрощается, а за dv выбирается множитель, содержащий dx, из которого интегрированием можно легко найти v.

Функции, интегрируемые по частям

Ø

где за u принимается u = P(x ) – многочлен целой степени.

Ø 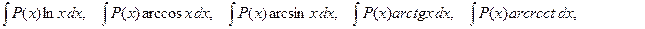u = lnx, u = arccosx, u = arcsinx, u = arctgx, u = arcctgx.

Ø

Ø Формулу интегрирования по частям можно применять неоднократно.

Интегрирование рациональных дробей

· Если числитель является производной знаменателя, то интеграл равен логарифму натуральному от знаменателя.

· Квадратный трехчлен в знаменателе можно разложить на линейные множители, а подынтегральную функцию на простые рациональные дроби:

коэффициенты А и В находят методом неопределенных коэффициентов.

· Квадратный трехчлен в знаменателе нельзя разложить на линейные множители, тогда следует выделить полный квадрат:

После чего вводят новую переменную.

Эти интегралы можно вычислить: первый – подведением под знак дифференциала, второй – непосредственным интегрированием.

Интегрирование тригонометрических функций

· Использование формул понижения степени:

· Подведение функции под знак дифференциала:

· Выделение четной степени и сведение к одной функции.

· Использование формулы произведения для интегралов вида:

.