Категории:

Дом Здоровье Зоология Информатика Искусство Искусство Компьютеры Кулинария Маркетинг Математика Медицина Менеджмент Образование Педагогика Питомцы Программирование Производство Промышленность Психология Разное Религия Социология Спорт Статистика Транспорт Физика Философия Финансы Химия Хобби Экология Экономика Электроника

Автоматизация научных исследований

Введение

Автоматизированные системы, использовавшиеся для управления сложными объектами, производственными и технологическими процессами, в настоящее время находят всё более широкое применение в такой области человеческой деятельности, как научные исследования. Уровень и быстрота научных разработок непосредственно влияют на научно-технический потенциал общества и, в свою очередь, зависят в значительной мере от степени автоматизации экспериментов и комплексных исследований. Сложные процессы в таких объектах глобального масштаба, как океан, земная поверхность или космос, требуют уже хотя бы из-за объемности исследования автоматизированной обработки информации. Ряд исследований из-за недоступности объектов вообще невозможен без использования автоматизированных систем. Поэтому создание и широкое внедрение автоматизированных систем научных исследований (АСНИ) представляют одну из важных инженерно-технических проблем.

Развитие научных направлений настолько многообразно, что создание единой универсальной АСНИ в обозримом будущем невозможнои, пожалуй, нецелесообразно. Однако единый подход к созданию и использованию совместного ряда АСНИ с применением стандартной аппаратуры (например, стандарт КАМАК и др.) абсолютно необходим, что и предусматривается комплексными программами "Автоматизация научных исследований".

Аппаратно-программная часть АСНИ, таким образом, может быть рассмотрена с некоторых единых позиций на основе стандартизации функциональных модулей аппаратуры, использования совместимого программного обеспечения, разработки проблемно-ориентированных комплексов по отдельным направлениям научных исследований и др. Разработанные методы и средства обеспечивают описание процессов обработки данных, отладку и исследование программно-аппаратных компонентов АСНИ, реализуемых в виде систем функционального моделирования. Для исследования реальных автоматизированных систем разрабатываются их цифровые модели, в том числе имитаторы внешней среды, позволяющие решать задачи по конструированию аппаратуры и отладке программного обеспечения. Вместе с тем общая модель системы не может отразить всю специфику объекта исследования, имеющего часто достаточно сложную структуру и невсегда поддающегося математическому описанию в приемлемой форме.

Поэтому кроме модели АСНИ, используемой в первую очередь для создания самой системы, необходимо при организации и проведении научных исследований иметь математическую модель экспериментального исследования объекта или внешней среды. Как правило, именно особенности модели объекта исследования определяют структуру технических и программных средств АСНИ. Это приводит к необходимости рассмотрения в процессе изучения этих систем моделей разного уровня: от моделей систем до моделей элементов исследуемых объектов. При проектировании важно анализировать эти модели с использованием системного подхода, с учетом их функционального взаимодействия в рамках единой АСНИ.

Математические модели АСНИ

Функциональные задачи АСНИ

В общем случае из-за разнообразия объектов исследования классификация АСНИ затруднена, тем неменее ряд классификационных признаков позволяет учесть их различия. Так, можно выделить следующие классификационные признаки АСНИ:

- по виду эксперимента (и, следовательно, моделям объектов): физико-химические эксперименты, медико-биологические и космические исследования, комплексные технические испытания сложных объектов, исследование природных ресурсов Земли и др.;

- по выполняемым функциям: технологические, организационно-технологические;

- по структуре построения: моноцентральные, иерархические, децентрализованные ;

- по методике проведения эксперимента: с математическим экспериментом, с имитационным экспериментом, с натурным экспериментом и со смешанным экспериментом.

Классификация, безусловно, может быть продолжена с учетом характера решаемых задач, роли человека-оператора, использования вычислительной техники. В любом случае большинство АСНИ разрабатывается индивидуально для решения определенного круга задач и исследования конкретных объектов. Использование аппаратуры с определенным стандартным набором функциональных модулей позволяет применять ее для решения целого круга исследовательских задач, сводя при этом разработку системы к созданию программно-алгоритмического и информационного обеспечения. Применение стандартных систем позволяет в определенной мере обобщить структуру АСНИ. Обобщенная структурная схема АСНИ включает в себя технические средства и обеспечивающие подсистемы.

Технические средства содержат экспериментальную установку или объект исследования с набором датчиков измерительной информации, осуществляющие сбор и преобразование информации. В состав технических средств входят также устройства сопряжения и средства передачи данных, средства обработки информации в виде ЭВМ или спецпроцессоров, а также средства регистрации и отображения информации .

К обеспечивающим подсистемам АСНИ можно отнести информационное и программно-математическое обеспечение. Информационное обеспечение содержит формализованное описание объектов, информационных источников и измерительных данных, а также информационную базу с системой создания и ведения информационных массивов.

Программно-математическое обеспечение может быть разделено на машинное, включающее операционную систему, систему программирования и тесты; общесистемное, содержащее управляющие диспетчерские программы и библиотеку стандартных программ; специальное, включающее программы и алгоритмы решения задач исследования, а также математические методы и математические модели.

Таким образом, математические методы и модели входят составной частью в обеспечивающую подсистему АСНИ. В зависимости от объекта исследования эта часть системы будет простой или чрезвычайно сложной, требующей на разработку больших усилий. В любом случае составление математических моделей на основе привлекаемых математических методов представляет собой наиболее сложную творческую часть разработки автоматизированной системы.

Среди общих функциональных задач, решаемых при разработке и реализации экспериментов с АСНИ, модели занимают важное место. Так, рассматривая последовательность задач, решаемых в процессе разработки и осуществления исследований, можно выделить следующий ряд процедур: планирование эксперимента,подготовку эксперимента, проведение исследований и обработку результатов.

Планирование эксперимента включает в себя:

- определение цели эксперимента;

- выбор информационных параметров;

- отбор управляющих параметров объекта или процесса;

- составление модели исследуемого процесса или явления;

- разработку на основе модели плана эксперимента.

Подготовка эксперимента подразумевает:

- разработку требований к средствам проведения эксперимента с учетом составленной модели;

- выбор и подготовку технических средств эксперимента;

- разработку программных средств управления экспериментом.

Проведение исследований осуществляется путем:

- сбора и регистрации информации в процессе исследования;

- взаимодействия экспериментатора с техническими средствами в ходе эксперимента с целью управления и коррекции.

Обработка результатов исследования включаетв себя :

- разработку алгоритма обработки результатов эксперимента с учётом модели объекта или процесса;

- разработку программного обеспечения;

- обработку результатов исследования;

- интерпретацию результатов исследования;

- корректировку модели процесса или явления.

Как видно из перечисленных задач, модель, разрабатываемая на стадии планирования эксперимента, является основой для построения автоматизированной системы подготовки и проведения исследований.

Модели изображений

Для анализа изображений используется три основных вида моделей формирования.

1. Непрерывная модель, при которой процесс преобразования рассматривается как непрерывный и изображение получается после искажения оператором h(x, y, e, h) реального оригинала f(e, h) и воздействия аддитивного шума n(x, y):

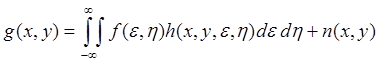. (2.1)

Это общее соотношение предполагает, что импульсная характеристика h(x, y, e, h) может изменяться в поле изображения, то есть быть пространственно зависимой. Во многих реальных системах h(x, y, e, h) является неизменной в поле изображений, то есть пространственно инвариантной, и модель формирования изображения в этом случае описывается в виде:

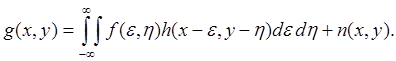(2.2)

Это соотношение представляет собой интеграл свёртки по двум пространственным координатам.

2. Непрерывно-дискретная модель предполагает, что оригинал непрерывен, а изображение представляется в виде отдельных дискретных отсчётов. В этом случае система формирования представляется соотношением

, (2.3)

где N – число отсчётов по одной координате;

h_i – импульсная характеристика (функция рассеивания точки) каждого элемента.

Дискретность вносится датчиком, который имеет мозаичную (матричную) структуру с импульсной характеристикой h₀. Для полного изображения предполагается формирование по двум координатам, т.е. по строкам и столбцам.

3. Дискретная модель предполагает, что уже оригинал изображения получается в дискретном виде путём растрового сканирования или другим способом в виде N x N отсчётов. Оригинал и изображение могут быть представлены в виде одномерных векторов 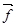и , а импульсная характеристика h(x,y,e,h) за счёт сканирования преобразуется в двумерную матрицу 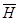. Тогда дискретное изображение на выходе системы формирования запишется в виде:

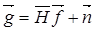, (2.4)

где - вектор шумовой помехи.

Для формирования реальных изображений могут использоваться комбинации приведенных выше моделей.

Модели непрерывных изображений

Изображение представляет собой двумерную систему, поэтому преобразование над изображениями описывается набором двумерных преобразований. Так, если f₁(x,y),...,f_N (x,y) представляет собой набор исходных двумерных функций оригинала, то с помощью набора операторов O_m ( ) можно записать выходные функции, т.е. изображения g₁(x,y),...,g_M(x,y) в виде:

При этом М и N могут иметь произвольные соотношения, а при M=N=1 получим соотношение g(x,y)=O{f(x,y)}. Модель получения изображения для пространственно инвариантной импульсной характеристики может быть представлена в виде соотношения:

, (2.5)

где d( x-e, y-h) - d-функция, расположенная в координатных осях (x,y) и имеющая координаты соответственно e и h (см. рис.2.5).

Рис.2.5

В выражении (2.5) отражены фильтрующие свойства d-функции, которые проявляются в том, что амплитуда d-функции в каждой точке пространства равна значению функции f(e,h).

Изменяя порядок действия линейного оператора О, получаем следующее соотношение:

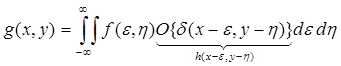. (2.6)

Таким образом, оператор О осуществляет искажение d-функции так, что в результате получается импульсная характеристика h или функция рассеивания точки, что приводит к рассмотренному ранее соотношению для формирования изображения

. (2.7)

Физически процесс формирования изображения можно представить на рис. 2.6,

Рис 2.6

где f(e,h) - неискажённый объект;

h(e,h) - функция рассеивания точки;

h(-e,-h) - функция рассеивания точки в инвертированных координатах.

Как видно из рисунка, в заштрихованной области произведение f(e,h)h(x-e, y-h)¹0 и интегрирование по ней даёт размытость непрерывного изображения на границах реального сформированного изображения g(x,y).

2.4. Двумерные спектральные преобразования

При формировании изображений

Модель двумерного непрерывного изображения позволяет осуществить переход с помощью двумерного преобразования Фурье в области пространственных частот w_x и w_y, у которых обычно используемый временной аргумент t заменяется на пространственный x,y. Двумерное преобразование Фурье имеет вид:

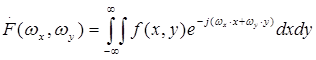, (2.8)

где

x, y - пространственные координаты изображений;

w_х и w_у - пространственные частоты;

f(x,y) - изображение .

В символическом виде преобразование Фурье можно записать в виде .

В общем случае спектр является комплексной величиной и его можно представить в виде:

где - амплитудно-частотная характеристика,

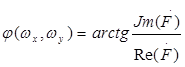- фазочастотная характеристика.

Исходный вид изображения может быть восстановлен с помощью обратного преобразования Фурье:

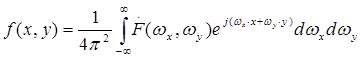(2.9)

или в символическом виде:

Так как ядро двумерного преобразования Фурье разделимо, то определение спектра может осуществляться в два этапа.

На первом этапе вычисляется спектр по оси х:

На втором этапе вычисляется спектр по оси у:

Двумерное преобразование Фурье обладает рядом важных свойств, которые переносятся на изображение, представляемое в виде преобразования Фурье.

1. Свойство линейности заключается в выполнении следующего соотношения :

; (2.10)

2. Свойство изменения масштаба представляется формулой:

. (2.11)

Из (2.11) видно, что изменение масштаба пространственных переменных приводит к обратному изменению масштаба пространственных частот. Сжатие изображения вдоль оси х или у приводит к растяжению вдоль соответствующей оси частотной плоскости и наоборот.

3. Сдвиг или смещение координат на плоскости х, у приводит к фазовым изменениям на частотной плоскости:

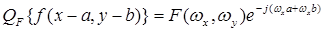. (2.12)

И обратно сдвиг частотной плоскости вызывает фазовые изменения исходной пространственной плоскости:

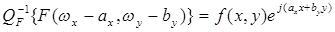. (2.13)

4. Энергия изображения может быть выражена через функцию изображения f(x,y) или спектр этого изображения F(w_x, w_y). При этом они равны, что определяется теоремой Парсеваля:

. (2.14)

5. Свёртка изображений – это наиболее распространённый вид обработки изображений. Фактически это реализация интеграла свёртки в частотной области.

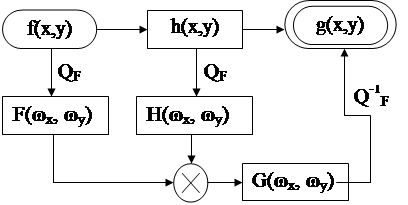Рис. 2.7.

Процедура формирования изображений по заданному объекту f(x,y) и

заданной импульсной характеристике схемы формирования h(x,y) математически удобно вычислять в частотной плоскости, как это иллюстрируется на рис.2.7, где

f(x,y) – оригинал изображения;

F(ω_x, ω_y) – Фурье-образ оригинала;

h(x,y) – функция рассеивания точки (ФРТ);

H(ω_x, ω_y) – Фурье-образ импульсной характеристики;

G(ω_x, ω_y) – Фурье-образ изображения;

Q_F – прямое преобразование Фурье;

Q^-1_F – обратное преобразование Фурье.

Фурье-образ изображения легко получается обычным перемножением:

G(ω_x, ω_y) = F(ω_x, ω_y)H(ω_x, ω_y),

откудно видно, что H(ω_x, ω_y) является фактически передаточной функцией схемы формирования изображений. А сформированное изображение получается из соотношения

g(x,y) = Q^-1_F{G(ω_x, ω_y)}.

Такой путь формирования изображений часто оказывается проще, чем вычисление интеграла свертки.

Дискретизация изображений

При цифровой обработке изображений последовательные ЭВМ работают с массивом чисел, получаемых путём дискретизации реальных непрерывных изображений по пространственным координатам. При анализе изображений их обычно рассматривают с двух точек зрения:

- как детерминированные поля, к которым применимы поэлементные преобразования и возможен спектральный анализ;

- как реализация двумерного случайного процесса. При этом могут вычисляться статистические характеристики изображения, такие как математическое ожидание, дисперсия, законы распределения, и может исследоваться влияние случайных шумов или помех. Рассматривается процесс дискретизации детерминированного изображения, который описывается с помощью дискретизирующей двумерной δ-функции в бесконечных пределах,

,

где Δx и Δy – шаг дискретизации соответственно по x и y.

На рис.2.8 показан процесс дискретизации непрерывного изображения f(x,y), а стрелками показаны значения отсчетов дискретизированного изображения f_d(x,y).

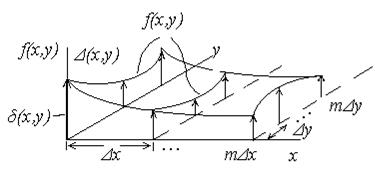Рис. 2.8

Таким образом, дискретизированное изображение получается из непрерывного в виде:

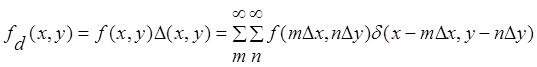, (2.15)

где используется фильтрующее свойство d-функции по пространству непрерывного изображения.

Если обозначить F_d(ω_x, ω_y)=Q_f{f_d(x,y)} – пространственный спектр дискретизованного изображения, F(ω_x, ω_y)=Q_f{f(x,y)} – спектр непрерывного изображения, S(ω_x, ω_y)=Q_f{Δ(x,y)} – преобразование Фурье от двумерной дискретизирующей функции, то соотношение между ними в частотной области определяется как свёртка:

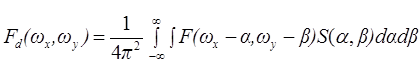, (2.16)

где α и β – параметры интегрирования.

Фурье представление сигналов

Каждая строка или столбец цифрового изображения могут рассматриваться в процессе обработки как одномерный сигнал с дискретными отсчетами. Однако для удобства изложения спектрального анализа вначале целесообразно рассмотреть аналоговую форму представления.

Непрерывный сигнал произвольной формы может быть представлен в виде суммы множества синусоид и косинусоид различной амплитуды:

,

где t - текущее время, а применительно к изображениям может рассматриваться как координата строки или столбца;

a₀ - постоянная составляющая сигнала;

а_n и b_n - коэффициенты Фурье (амплитуды) n-х гармоник соответствующих синусных и косинусных периодических функций;

w₀ (рад/с) - основная угловая частота (для изображений это пространственная частота), , Т - период основной (пространственной) частоты f, от которого отсчитываются все гармоники.

Коэффициенты Фурье определяются из соотношений

; ; .

Таким образом, следует, что сигнал x(t), заданный на интервале Т, приведенный, например, на рис.3.1, может быть представлен набором действительных чисел

{a₀, a_n, b_n}. Если исходную функцию представить набором гармонических функций вкомплексной форме:

Рис.3.1 , тогда сам сигнал x(t) можно представить в с помощью комплексного коэффициента в виде

, где . (3.1)

При этом связь с коэффициентами Фурье выражается соотношениями

; .

Для периодического сигнала x_p(t) с периодом Т и для заданного смещения t разложенный по комплексному ряду Фурье-сигнал, приведенный на рис.3.2, может быть представлен в виде

.

Рис.3.2

При этом не зависит от времени t и, следовательно, на спектр разложения не влияет, то есть его можно представить в виде

. Эта величина называется мощностью n-й гармонической составляющей и обладает такими свойствами, как инвариантность величине временного сдвига, неотрицательность, и является чётной функцией n, так как .

Амплитудный Фурье-спектр , n=1,±1,±2,...

Фазовый Фурье-спектр периодического сигнала определяется для каждой гармоники соотношением

,

где - мнимая часть коэффициента;

- действительная часть коэффициента.

Фазовый Фурье-спектр обладает следующими свойствами :

спектр y_n является функцией сдвига t, то есть изменяется при сдвиге сигнала вдоль оси времени; он не зависит от ослабления или усиления сигнала по амплитуде, в то время как спектр мощности P_n является функцией усиления; y_n является нечётной функцией n, так как y_-_n= -y_n.

3.2. Преобразование Фурье

Рассмотрим переход от ряда Фурье к преобразованию Фурье на конкретном примере .

Раскладывается периодическая функция х_р(t), приведенная на рис.3.3, в комплексный ряд Фурье:

,

где коэффициент разложения вычисляется в виде Рис.3.3

, (3.2)

n=0,±1,...

Для случая непрерывного сигнала, то есть при Т®¥, последовательность импульсов будет вырождаться в единственный импульс, то есть в апериодическую функцию x(t).

Из рис.3.3 видно, что при Т®¥ спектр линий сжимается и превращается в непрерывную функцию - огибающую вида sinx/x.

Коэффициент Фурье, выражающийся в виде и при Т®¥ изменится, и его составляющие станут w₀®dw, nw₀®w, т.е. n-я гармоника становится непрерывной угловой частотой, а , где F(w) - непрерывная функция, которая представляет собой преобразование Фурье непрерывной функции x(t),

. (3.3)

Само разложение для периодической функции Х_р(t), имеющее вид

, изменится, и при T®¥ суммирование по всем гармоникам можно заменить интегрированием по всем частотам соответственно dw; nw₀®w; , так что разложение будет иметь вид

.

Это соотношение называется обратным преобразованием Фурье, оно позволяет вычислить исходную функцию времени по известному преобразованию .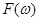

Для преобразования Фурье вводятся понятия:

- спектр мощности ;

- амплитудный спектр , который может быть разложен на действительную и мнимую части F(w)=A(w)+jB(w);

- фазовый спектр .

3.3. Дискретное преобразование Фурье (ДПФ)

Для представления дискретных сигналов, то есть дискретных или цифровых последовательностей, вводится понятие дискретного преобразования Фурье. Обозначается {X(m)} - последовательность конечных действительных или комплексных чисел X(m), .

Дискретное преобразование Фурье для такой последовательности определяется в виде

, (3.4)

где - экспоненциальные функции, обладающие условием ортогональности:

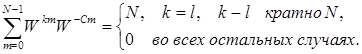
Обратное дискретное преобразование Фурье определяется формулой

, (3.5)

то есть существуют эквивалентность перехода и однозначная связь X(m)ÛC_x(k).

Функции W^km являются периодическими с периодом повторения дискретной последовательности N:

W^km=W^(k+N)m=W^k(m+N), km = 0, ±1, ±2,...

Значит, последовательности {C_x(k)}, {X(m)} являются N-периодическими, т.е.

X(±m)=X(SN±m),

C_x(±k)= C_x (SN±k), S=0,±1, ±2….

Поэтому суммы дискретных преобразований Фурье можно брать в любых интервалах, но так, чтобы разность между нижним и верхним пределами была N-1.

Дискретное преобразование Фурье имеет свойства, широко используемые при обработке цифровых изображений.

1.Свойство линейности

Теорема линейности говорит о том, что ДПФ является линейным преобразованием, т.е. если Х(m)«C_x(k), где Х(m) – временная последовательность, а С_x(k) – коэффициенты ДПФ, то для новой последовательности Z(m)=aX(m)+bY(m) коэффициенты ДПФ определяются как C_z(k)=aC_x(k)+bC_y(k). (3.6)

2.Свойство комплексной сопряжённости

Если в последовательности {X(m)}={x(0),x(1),...,x(N-1)} действительных чисел N/2 будет целым числом, тогда при отсчете от середины N/2 в обе стороны коэффициенты Фурье будут комплексно-сопряжёнными для любых l=1,2,...,N/2, то есть

С_X(N/2+l)=C_X^*(N/2-l). (3.7)

Сдвиг последовательности

Если X(m)«C_X(k), тогда для Z(m)=X(m+h), 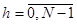коэффициенты ДПФ определяются соотношением

С_Z(k)=W^-khC_x(k). (3.8)

Свёртка последовательности

Если {X(m)} и {Y(m)} – последовательности, для которых коэффициенты ДПФ вычислены соответственно X(m)«C_x(k) и Y(m)«C_y(k), то свёртка последовательности определяется соотношением

, , (3.9)

тогда коэффициенты вычисляются в виде

С_z(k)=C_x(k)C_y(k). (3.10)

Таким образом свертка временных последовательностей эквивалентна умножению их коэффициентов ДПФ.

Библиографический список

1. Виттих В.А., Сергеев А.В., Сойфер В.А. Обработка изображений в автоматизированных системах научных исследований. М.: Наука, 1982.

2. Ярославский Л.Н. Введение в цифровую обработку изображений. М.: Сов.радио, 1979.

3. Ахмед Н., Рао К.Р. Ортогональные преобразования при обработке цифровых сигналов. М.: Связь, 1980.

4. Дондик Е.М. Математические методы АСНИ: Сб. Учеб.пособие. Рязань: РРТИ, 1989.

ОГЛАВЛЕНИЕ

Введение...................................................................................................................................... 1

1.Математические модели АСНИ....................................................................................... 2

1.1. Автоматизация научных исследований........................................................... 2

1.2. Функциональные задачи АСНИ........................................................................... 3

1.3. Виды математических моделей АСНИ.............................................................. 5

2. Формирование и структура изображений..................................................................... 7

2.1. Методы формирования изображений................................................................. 7

2.2. Модели изображений............................................................................................... 9

2.3.Модели непрерывных изображений.................................................................. 10

2.4. Двумерные спектральные преобразования при формировании

изображений.................................................................................................................... 12

2.5. Дискретизация изображений............................................................................... 14

2.6.Дискретизация реальных изображений........................................................... 17

2.7.Восстановление непрерывных изображений................................................ 18

2.8.Матричное представление дискретных изображений................................ 21

2.9.Элементарные операции с дискретными изображениями........................ 23

2.10.Обращение и транспонирование изображений............................................ 25

2.11.Матричные и векторные характеристики изображений.......................... 26

3. Спектральный анализ изображений............................................................................. 29

3.1.Фурье представление сигналов.......................................................................... 29

3.2. Преобразование Фурье.......................................................................................... 31

3.3. Дискретное преобразование Фурье (ДПФ)...................................................... 32

3.4. Быстрое преобразование Фурье (БПФ)............................................................ 34

Библиографический список................................................................................................ 40

Дондик Евгений Михайлович

Редактор И.П. Перехрест

Корректор Н.А. Орлова

Лицензия № 020446.

Подписано в печать 22.07.02.Формат бумаги 60´84 1/16.

Бумага газетная. Печать трафаретная. Усл. печ. л. 2,5.

Уч.-изд.л. 2,5. Тираж 25 экз. Заказаказ 093 Ц. 50 р.

Рязанская государственная радиотехническая академия.

390005, Рязань, ул. Гагарина, 59/1.

Редакционно-издательский центр РГРТА.

Введение

Автоматизированные системы, использовавшиеся для управления сложными объектами, производственными и технологическими процессами, в настоящее время находят всё более широкое применение в такой области человеческой деятельности, как научные исследования. Уровень и быстрота научных разработок непосредственно влияют на научно-технический потенциал общества и, в свою очередь, зависят в значительной мере от степени автоматизации экспериментов и комплексных исследований. Сложные процессы в таких объектах глобального масштаба, как океан, земная поверхность или космос, требуют уже хотя бы из-за объемности исследования автоматизированной обработки информации. Ряд исследований из-за недоступности объектов вообще невозможен без использования автоматизированных систем. Поэтому создание и широкое внедрение автоматизированных систем научных исследований (АСНИ) представляют одну из важных инженерно-технических проблем.

Развитие научных направлений настолько многообразно, что создание единой универсальной АСНИ в обозримом будущем невозможнои, пожалуй, нецелесообразно. Однако единый подход к созданию и использованию совместного ряда АСНИ с применением стандартной аппаратуры (например, стандарт КАМАК и др.) абсолютно необходим, что и предусматривается комплексными программами "Автоматизация научных исследований".

Аппаратно-программная часть АСНИ, таким образом, может быть рассмотрена с некоторых единых позиций на основе стандартизации функциональных модулей аппаратуры, использования совместимого программного обеспечения, разработки проблемно-ориентированных комплексов по отдельным направлениям научных исследований и др. Разработанные методы и средства обеспечивают описание процессов обработки данных, отладку и исследование программно-аппаратных компонентов АСНИ, реализуемых в виде систем функционального моделирования. Для исследования реальных автоматизированных систем разрабатываются их цифровые модели, в том числе имитаторы внешней среды, позволяющие решать задачи по конструированию аппаратуры и отладке программного обеспечения. Вместе с тем общая модель системы не может отразить всю специфику объекта исследования, имеющего часто достаточно сложную структуру и невсегда поддающегося математическому описанию в приемлемой форме.

Поэтому кроме модели АСНИ, используемой в первую очередь для создания самой системы, необходимо при организации и проведении научных исследований иметь математическую модель экспериментального исследования объекта или внешней среды. Как правило, именно особенности модели объекта исследования определяют структуру технических и программных средств АСНИ. Это приводит к необходимости рассмотрения в процессе изучения этих систем моделей разного уровня: от моделей систем до моделей элементов исследуемых объектов. При проектировании важно анализировать эти модели с использованием системного подхода, с учетом их функционального взаимодействия в рамках единой АСНИ.

Математические модели АСНИ

Автоматизация научных исследований

Наука в наше время является одной из основных движущих сил технического прогресса. Ускоренное внедрение научных исследований непосредственно создает условия для динамичного развития производительных сил общества. Это справедливо для всех научных направлений, но в первую очередь для комплексных исследований таких объектов, как океан, земная поверхность, космос и т.д. Изучение их вследствие объемности, а также сложности протекающих процессов представляет собой достаточно трудную задачу, тем более что необходимая информация, как правило, превышает возможности человеческого восприятия. Поэтому автоматизация процесса обработки научной информации является едва ли не единственным средством, позволяющим обобщать результаты, устанавливать закономерности, делать выводы.

Наука развивается по множеству направлений, поэтому и научные исследования настолько многообразны, что изучать их полностью с единых позиций и едиными методами весьма затруднительно. Необходима определенная привязка к объектам исследования. Следовательно, в процессе изучения и проектирования АСНИ можно выделить объектный уровень рассмотрения, при котором делается упор на динамические, статистические или другие модели объекта исследования, и системный уровень, предполагающий системотехнический анализ функциональных модулей, разработку программно-алгоритмического обеспечения системы и т.д.

Научные исследования вообще подразделяются на два направления - теоретические и экспериментальные. Хотя принципиально для обоих направлений существует возможность автоматизации, однако теоретические исследо

12 3 4 5