Матричные и векторные характеристики изображений

Следом квадратной матрицы размером NxN называется сумма ее диагональных элементов

tr[ ]= .

Для двух квадратных изображений справедливо соотношение

tr[ ]=tr[ ]. (2.47)

След прямого произведения двух матричных изображений определяется в виде

tr[ ]=tr( )tr( 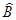). (2.48)

Нормой матрицы произвольного размера называется скаляр, определяемый как

.

Нормой вектора размером Nx1 называется скаляр определяемый в виде

.

Скалярным произведением векторов и размером Nx1 является скаляр, определяемый как

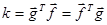(2.49)

или для элементов

.

Матричным произведением векторов размером Мх1 и размером Nx1 является матрица

,

где элементы матрицы определяются как

A(m,n)=g(m) f(n). (2.50)

Квадратичной формой вектора размером Nx1 является скаляр

,

где - матрица размером NxN. Обычно матрица берется симметричной.

Для анализа изображений иногда удобно перейти от матричного представления

размерностью (N₁xN₂)

к векторному, собирая элементы столбцов (или строк) матрицы в один вектор большой размерности.

Формально эту операцию можно представить с помощью вспомогательного вектора размером (N₂x1) и матрицы размером (N₁N₂xN₁), которые определяются в виде

, . (2.51)

В этом случае матрица будет определена в векторной форме с помощью операции упорядочения как

. (2.52)

Вектор выделяет n-й столбец матрицы , а матрица помещает этот столбец на место, отведенное для n-го отрезка вектора . Таким образом, вектор содержит все элементы матрицы , последовательно считанные по столбцам.

Обратная операция преобразования вектора в матрицу описывается соотношением

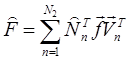. (2.53)

Формулы (2.52) и (2.53) устанавливают однозначную связь между матричным и векторным представлением изображений.

Достоинствами векторного представления изображений являются большая компактность обозначений, а также возможность анализа последовательной обработки на основании методов, разработанных для одномерных сигналов. Однако векторное представление имеет существенный недостаток – учитывается корреляция элементов изображения только вдоль столбцов или строк, а не всего изображения, как это существует в реальности.

Спектральный анализ изображений

Фурье представление сигналов

Каждая строка или столбец цифрового изображения могут рассматриваться в процессе обработки как одномерный сигнал с дискретными отсчетами. Однако для удобства изложения спектрального анализа вначале целесообразно рассмотреть аналоговую форму представления.

Непрерывный сигнал произвольной формы может быть представлен в виде суммы множества синусоид и косинусоид различной амплитуды:

,

где t - текущее время, а применительно к изображениям может рассматриваться как координата строки или столбца;

a₀ - постоянная составляющая сигнала;

а_n и b_n - коэффициенты Фурье (амплитуды) n-х гармоник соответствующих синусных и косинусных периодических функций;

w₀ (рад/с) - основная угловая частота (для изображений это пространственная частота), , Т - период основной (пространственной) частоты f, от которого отсчитываются все гармоники.

Коэффициенты Фурье определяются из соотношений

; ; .

Таким образом, следует, что сигнал x(t), заданный на интервале Т, приведенный, например, на рис.3.1, может быть представлен набором действительных чисел

{a₀, a_n, b_n}. Если исходную функцию представить набором гармонических функций вкомплексной форме:

Рис.3.1 , тогда сам сигнал x(t) можно представить в с помощью комплексного коэффициента в виде

, где . (3.1)

При этом связь с коэффициентами Фурье выражается соотношениями

; .

Для периодического сигнала x_p(t) с периодом Т и для заданного смещения t разложенный по комплексному ряду Фурье-сигнал, приведенный на рис.3.2, может быть представлен в виде

.

Рис.3.2

При этом не зависит от времени t и, следовательно, на спектр разложения не влияет, то есть его можно представить в виде

. Эта величина называется мощностью n-й гармонической составляющей и обладает такими свойствами, как инвариантность величине временного сдвига, неотрицательность, и является чётной функцией n, так как .

Амплитудный Фурье-спектр , n=1,±1,±2,...

Фазовый Фурье-спектр периодического сигнала определяется для каждой гармоники соотношением

,

где - мнимая часть коэффициента;

- действительная часть коэффициента.

Фазовый Фурье-спектр обладает следующими свойствами :

спектр y_n является функцией сдвига t, то есть изменяется при сдвиге сигнала вдоль оси времени; он не зависит от ослабления или усиления сигнала по амплитуде, в то время как спектр мощности P_n является функцией усиления; y_n является нечётной функцией n, так как y_-n = -y_n.

3.2. Преобразование Фурье

Рассмотрим переход от ряда Фурье к преобразованию Фурье на конкретном примере .

Раскладывается периодическая функция х_р(t), приведенная на рис.3.3, в комплексный ряд Фурье:

,

где коэффициент разложения вычисляется в виде Рис.3.3

, (3.2)

n=0,±1,...

Для случая непрерывного сигнала, то есть при Т®¥, последовательность импульсов будет вырождаться в единственный импульс, то есть в апериодическую функцию x(t).

Из рис.3.3 видно, что при Т®¥ спектр линий сжимается и превращается в непрерывную функцию - огибающую вида sinx/x.

Коэффициент Фурье, выражающийся в виде и при Т®¥ изменится, и его составляющие станут w₀®dw, nw₀®w, т.е. n-я гармоника становится непрерывной угловой частотой, а , где F(w) - непрерывная функция, которая представляет собой преобразование Фурье непрерывной функции x(t),

. (3.3)

Само разложение для периодической функции Х_р(t), имеющее вид

, изменится, и при T®¥ суммирование по всем гармоникам можно заменить интегрированием по всем частотам соответственно dw; nw₀®w; , так что разложение будет иметь вид

.

Это соотношение называется обратным преобразованием Фурье, оно позволяет вычислить исходную функцию времени по известному преобразованию .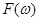

Для преобразования Фурье вводятся понятия:

- спектр мощности ;

- амплитудный спектр , который может быть разложен на действительную и мнимую части F(w)=A(w)+jB(w);

- фазовый спектр .

3.3. Дискретное преобразование Фурье (ДПФ)

Для представления дискретных сигналов, то есть дискретных или цифровых последовательностей, вводится понятие дискретного преобразования Фурье. Обозначается {X(m)} - последовательность конечных действительных или комплексных чисел X(m), .

Дискретное преобразование Фурье для такой последовательности определяется в виде

, (3.4)

где - экспоненциальные функции, обладающие условием ортогональности:

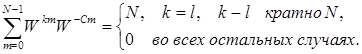
Обратное дискретное преобразование Фурье определяется формулой

, (3.5)

то есть существуют эквивалентность перехода и однозначная связь X(m)ÛC_x(k).

Функции W^km являются периодическими с периодом повторения дискретной последовательности N:

W^km =W^(k+N)m =W^k(m+N), km = 0, ±1, ±2,...

Значит, последовательности {C_x(k)}, {X(m)} являются N-периодическими, т.е.

X(±m)=X(SN±m),

C_x(±k)= C_x (SN±k), S=0,±1, ±2….

Поэтому суммы дискретных преобразований Фурье можно брать в любых интервалах, но так, чтобы разность между нижним и верхним пределами была N-1.

Дискретное преобразование Фурье имеет свойства, широко используемые при обработке цифровых изображений.

1.Свойство линейности

Теорема линейности говорит о том, что ДПФ является линейным преобразованием, т.е. если Х(m)«C_x(k), где Х(m) – временная последовательность, а С_x(k) – коэффициенты ДПФ, то для новой последовательности Z(m)=aX(m)+bY(m) коэффициенты ДПФ определяются как C_z(k)=aC_x(k)+bC_y(k). (3.6)

2.Свойство комплексной сопряжённости

Если в последовательности {X(m)}={x(0),x(1),...,x(N-1)} действительных чисел N/2 будет целым числом, тогда при отсчете от середины N/2 в обе стороны коэффициенты Фурье будут комплексно-сопряжёнными для любых l=1,2,...,N/2, то есть

С_X(N/2+l)=C_X^*(N/2-l). (3.7)

Сдвиг последовательности

Если X(m)«C_X(k), тогда для Z(m)=X(m+h), 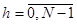коэффициенты ДПФ определяются соотношением

С_Z(k)=W^-khC_x(k). (3.8)

Свёртка последовательности

Если {X(m)} и {Y(m)} – последовательности, для которых коэффициенты ДПФ вычислены соответственно X(m)«C_x(k) и Y(m)«C_y(k), то свёртка последовательности определяется соотношением

, , (3.9)

тогда коэффициенты вычисляются в виде

С_z(k)=C_x(k)C_y(k). (3.10)

Таким образом свертка временных последовательностей эквивалентна умножению их коэффициентов ДПФ.