
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Амплитудный спектр и спектр мощности ДПФ
Если последовательность {X(m)} имеет коэффициенты ДПФ Cx(k), то существует соотношение
 , (3.13)
, (3.13)
называемое теоремой Парсеваля.
Левая часть равенства описывает среднюю за период мощность, рассеиваемую резистором, а величина ½Сx(k)½2 представляет собой мощность, содержащуюся в каждой гармонике, имеющей частоту с номером k. Спектр мощности ДПФ определяется:
P(k)=½Cx(k)½2,  .
.
Однако так как у ДПФ имеется только N/2 независимых спектральных точек при {X(m)} действительных, а остальные являются комплексно-сопряжёнными, мощность определяется только активной составляющей  , то есть спектр мощности является чётной функцией относительно точки k=N/2 и инвариантен к сдвигам N-периодической временной последовательности. Амплитудный спектр определяется соотношением
, то есть спектр мощности является чётной функцией относительно точки k=N/2 и инвариантен к сдвигам N-периодической временной последовательности. Амплитудный спектр определяется соотношением  . Фазовый спектр ДПФ определяется соотношением:
. Фазовый спектр ДПФ определяется соотношением: 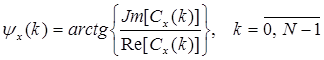 ,
,
где Jm, Re - соответственно мнимая и действительная части коэффициента ДПФ.
Главным свойством фазового спектра является его инвариантность к умножению {X(m)} последовательности на постоянную величину. Фазовый спектр представляет собой нечётную функцию относительно середины N/2 последовательности.
3.4. Быстрое преобразование Фурье (БПФ)
Быстрым преобразованием Фурье (БПФ) называется частный случай ДПФ с теми же формулами для определения коэффициентов разложения
 , (3.14)
, (3.14)
только число дискретных отсчётов должно быть N=2n,  , т.е. N=4,8,16,32,64,...
, т.е. N=4,8,16,32,64,...
Это условие не ограничивает возможности использования БПФ, так как N всегда выбирается достаточно большим, чтобы выдержать условие дискретизации, то есть N³2BL, где B – полоса частот сигнала x(t); L – длительность сигнала .Возможно использование БПФ и для N¹2n с помощью специальных приемов.
Рассматривается случай, когда N=8, 0£m£N-1.
Представляется каждое текущее значение отсчёта m в двоичной форме:
m=mn-12n-1+...mn2n+...+m121+m020, где  .
.
Аналогично выразится к.
ДПФ обладает свойством комплексной сопряжённости, поэтому для N=8 коэффициенты, отсчитываемые относительно k=4, окажутся равными, т.е.
Cx(4+l)=C*x(4-l), l=1,2,3.
Поэтому можно рассмотреть только k=0,1,2,3:
 , k=
, k=  , (3.15)
, (3.15)
где  .
.
Для рассматриваемого случая N=8=23, поэтому можно рассматривать только 3 разряда двоичных чисел:  ,
,
 ,
,
где m2, m1,m0,k2,k1,k0=  .
.
Например, при последовательности изменений m отсчетов m2, m1,m0 принимают обычные значения, приведенные в таблице.
| m | m2 | m1 | m0 |
Подставляя эти значения в формулу (3.15), можно получить граф для вычисления БПФ.
Пусть  - двоичное представление числа, тогда последовательно подставляя значения m, получаем следующее соотношение: - двоичное представление числа, тогда последовательно подставляя значения m, получаем следующее соотношение:
|
| 0 1 2 3 4 5 6 7 | 0 0 0 0 1 1 1 1 | 0 0 1 1 0 0 1 1 | 0 1 0 1 0 1 0 1 |
 , (3.16)
, (3.16)
где  - двоичное представление числа x(m).
- двоичное представление числа x(m).
При этом внутренняя сумма по m2 будет
 .
.
Так как 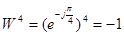 , тогда внутренняя сумма представится в виде
, тогда внутренняя сумма представится в виде
 .
.
Поскольку  , как чётная степень (-1), тогда
, как чётная степень (-1), тогда
 . (3.17)
. (3.17)
Подставив обозначение 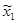 в (3.16), получим
в (3.16), получим
 . (3.18)
. (3.18)
Теперь рассматриваем внутреннее суммирование по m1:
 ,
,
а учитывая, что
 ,
,
получаем
 . (3.19)
. (3.19)
Суммирование по m1 приводит к функции, зависящей от k0, k1, m0:
 .
.
Подставив  в формулу (3.16), получим
в формулу (3.16), получим
 .
.
Обозначая последнюю сумму по m0 как М0 и учитывая, что  , получаем
, получаем
 . (3.20)
. (3.20)
Суммирование по m0 приводит к третьей итерации, т.е.  или
или
 .
.
Определим коэффициенты (-1), (-j),  в виде корня из
в виде корня из  , т.е.
, т.е.  .
.
Они являются соответственно корнями 2,4 и 8-й степени.
Введём обозначения  , где r=1,2,...,log2N, а
, где r=1,2,...,log2N, а  .
.
Рассмотрим первую сумму с учетом введенных обозначений
 . (3.21)
. (3.21)
Теперь, раскрывая первую сумму по m2, которая принимает значение 0 или 1, получаем
 ,
,
а так как  тоже принимает два значения, то для каждой k0 будет 4 уравнения при переменных m1 и m0.
тоже принимает два значения, то для каждой k0 будет 4 уравнения при переменных m1 и m0.
При k=0:  ,
,
 ,
,
 ,
,
 .
.
При k=1:  ,
,
 ,
,
 ,
,
 .
.
Общей формулы для вычисления промежуточных итераций нет, а результаты могут быть получены последовательно для каждой итерации.
Для первой итерации:
 , (3.22)
, (3.22)
где запишутся по 4 уравнения для k0 =0и k0=1.
Для второй итерации
 (3.23)
(3.23)
или
 . (3.24)
. (3.24)
Для каждой комбинации (k0,k1) будет по два уравнения
| (0,0) | 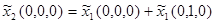 , ,
|
 ; ;
| |
| (0,1) |  , ,
|
 ; (3.25) ; (3.25)
| |
| (1,0) |  , ,
|
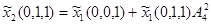 ; ;
| |
  (1,1) (1,1)
|  , ,
|
 . .
|
Для третьей итерации
 . (3.26)
. (3.26)
 Теперь можно построить граф последовательных вычислений для каждой итерации N=8. При этом возможны два варианта графа в зависимости от очередности следования отсчетов исходной дискретной последователь-ности. Если берется прямая последовательность отсчетов по строке или столбцу пространства изображений, то коэффициенты разложения получаются в двоично-инвертированной последовательнос-
Теперь можно построить граф последовательных вычислений для каждой итерации N=8. При этом возможны два варианта графа в зависимости от очередности следования отсчетов исходной дискретной последователь-ности. Если берется прямая последовательность отсчетов по строке или столбцу пространства изображений, то коэффициенты разложения получаются в двоично-инвертированной последовательнос-
ти, как это показано на рис.3.4, при этом коэффициенты БПФ следуют в прямой последовательности.
Рис.3.4
 Из структуры графа следует, что можно воспользоваться универсальной схемой вычисления значений каждой последующей итерации по двум предшествующим значениям, как это показано на рис.3.5, где использованы обозначения
Из структуры графа следует, что можно воспользоваться универсальной схемой вычисления значений каждой последующей итерации по двум предшествующим значениям, как это показано на рис.3.5, где использованы обозначения
C=A+WSB , D=A-WSB, а коэффициенты WS вычисляются
Рис.3.5 по формуле
 (3.27)
(3.27)
В приведенном графе вычисления БПФ коэффициенты не делятся на число отсчетов исходной последовательности N.
Вычисление обратного быстрого преобразования Фурье (ОБПФ) осуществляется по аналогичной методике с использованием такого же графа, при этом значения результатов делятся на N.
Дискретное преобразование Фурье можно обобщить на случай многомерного разложения, причем наиболее полезным оказывается обобщение на случай двумерного разложения, поскольку оно широко применяется при обработке изображений. Двумерное ДПФ определяется следующим соотношением
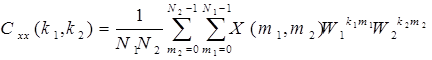 , (3.28)
, (3.28)
где  и
и  изменяются в пределах от 0 до
изменяются в пределах от 0 до 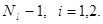 Массив данных образует матрицу
Массив данных образует матрицу  размером
размером  :
:
 . (3.29)
. (3.29)
Выражение внутренней суммы определяется как
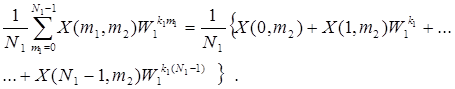 (3.30)
(3.30)
Откуда следует, что правая часть представляет собой ДПФ каждого столбца данных  , поэтому можно ввести обозначение
, поэтому можно ввести обозначение
 . (3.31)
. (3.31)
Коэффициенты 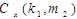 в выражении (3.31) можно записать в форме матрицы
в выражении (3.31) можно записать в форме матрицы  размером
размером  :
:
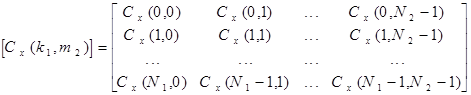 . (3.32)
. (3.32)
В результате подстановки (3.31) в выражение (3.28) получается выражение
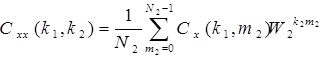 . (3.33)
. (3.33)
Это означает, что коэффициенты  получаются путем вычисления ДПФ каждой строки матрицы
получаются путем вычисления ДПФ каждой строки матрицы  , определенной выражением (3.32). В результате получается множество из
, определенной выражением (3.32). В результате получается множество из  коэффициентов, которые могут быть также записаны в виде матрицы
коэффициентов, которые могут быть также записаны в виде матрицы
 . (3.34)
. (3.34)
Из приведенных выше рассуждений следует, что двумерное ДПФ в выражении (3.28) можно рассматривать как  - кратное использование одномерного ДПФ.
- кратное использование одномерного ДПФ.
Важной стороной спектрального анализа является вычисление пространственно-частотных спектров изображений, получаемых на основе преобразования Фурье. Наиболее важными составляющими спектра изображений являются амплитудный и фазовый спектры. Амплитудный спектр, в общем, не содержит информации о наличии и положении световой границы, но в нем заключена информация о яркости и резкости изображения. Информация о положении световой границы, в основном, заключена в фазовом спектре. Изображение может быть подвергнуто значительным линейным и нелинейным искажениям, но если искажения фазового спектра при этом будут невелики, так что они не вызовут исчезновения или появления новых световых границ, изображение будет легко узнаваться. К таким искажениям относятся интегрирование (расфокусировка), дифференцирование (подчеркивание границ), поэлементные преобразования. Если же в результате преобразования существенно искажается фазовый спектр изображения, то может произойти полная потеря узнаваемости изображаемого объекта.
На основании изложенного можно сделать вывод, что при передаче изображений особое влияние следует уделять передаче фазового спектра.
Библиографический список
1. Виттих В.А., Сергеев А.В., Сойфер В.А. Обработка изображений в автоматизированных системах научных исследований. М.: Наука, 1982.
2. Ярославский Л.Н. Введение в цифровую обработку изображений. М.: Сов.радио, 1979.
3. Ахмед Н., Рао К.Р. Ортогональные преобразования при обработке цифровых сигналов. М.: Связь, 1980.
4. Дондик Е.М. Математические методы АСНИ: Сб. Учеб.пособие. Рязань: РРТИ, 1989.
ОГЛАВЛЕНИЕ
Введение...................................................................................................................................... 1
1.Математические модели АСНИ....................................................................................... 2
1.1. Автоматизация научных исследований........................................................... 2
1.2. Функциональные задачи АСНИ........................................................................... 3
1.3. Виды математических моделей АСНИ.............................................................. 5
2. Формирование и структура изображений..................................................................... 7
2.1. Методы формирования изображений................................................................. 7
2.2. Модели изображений............................................................................................... 9
2.3.Модели непрерывных изображений.................................................................. 10
2.4. Двумерные спектральные преобразования при формировании
изображений.................................................................................................................... 12
2.5. Дискретизация изображений............................................................................... 14
2.6.Дискретизация реальных изображений........................................................... 17
2.7.Восстановление непрерывных изображений................................................ 18
2.8.Матричное представление дискретных изображений................................ 21
2.9.Элементарные операции с дискретными изображениями........................ 23
2.10.Обращение и транспонирование изображений............................................ 25
2.11.Матричные и векторные характеристики изображений.......................... 26
3. Спектральный анализ изображений............................................................................. 29
3.1.Фурье представление сигналов.......................................................................... 29
3.2. Преобразование Фурье.......................................................................................... 31
3.3. Дискретное преобразование Фурье (ДПФ)...................................................... 32
3.4. Быстрое преобразование Фурье (БПФ)............................................................ 34
Библиографический список................................................................................................ 40
Дондик Евгений Михайлович
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...