
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Связь с сопряженным уравнением. Нормальная разрешимость.
Некоторые теоремы.
I. Пусть Т – вполне непрерывный оператор, действующий в банаховом пространстве Е1 с областью значений, принадлежащей банахову пространству Е2. Тогда для уравнения (I+T)x=y, где I – единичный оператор, xÎE1, yÎE2, справедлива теорема Фредгольма.
II. Пусть {xa} - некоторое множество элементов банахова пространства, пространства Е и {xa} - множество линейных ограниченных функционалов, определенных на пространстве Е. Эти два множества называются биортогональными, если xj(xi)=1 при i=j и xj(xi)=0 при i¹j. Имеют место следующие утверждения:
1. Пусть x1,x2,…,xn – первоначальная линейно-независимая система элементов пространства Е, тогда существует биортогональная система линейных ограниченных функционалов, т.е. в сопряженном пространстве Е* найдутся такие элементы x1,x2,…,xn, что
1 при i=j
 (0.1)
(0.1)
0 при i¹j
2. Пусть x1,x2,…,xn – произвольная линейно-независимая система линейных ограниченных функционалов над пространством Е, тогда найдутся такие элементы x1,x2,…,xn для которых выполняются соотношения (0.1).
II. Теорема Банаха. Если линейный ограниченный оператор В отображает все банахово пространство Е1 на все банахово пространство Е2 взаимно однозначно, то существует линейный ограниченный оператор В-1, обратный оператору В, отображающий Е2 на Е1.
IV. Пусть линейный ограниченный оператор В отображает банахово пространство Е в себя и ||B||bq<1. Тогда оператор I+B имеет обратный линейный ограниченный оператор.
V. Пусть в банаховом пространстве Е задано линейное многообразие X и элемент x0Ï  , находящийся на расстоянии d>0 от X
, находящийся на расстоянии d>0 от X 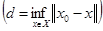 . Тогда существует функционал f(x), определенный всюду на Е и такой, что f(x)=0 для xÎX, f(x0)=1.
. Тогда существует функционал f(x), определенный всюду на Е и такой, что f(x)=0 для xÎX, f(x0)=1.
VI. Если для элемента x банахова пространства Е и всех функционалов f, определенных на этом пространстве, выполнено соотношение f(x)=0, то x=0.
VII. Если пространство Е бесконечномерно, то единичный шар F не компактен.
VIII. Если А – вполне непрерывный оператор, отображающий банахово пространство Е1 в банахово пространство Е2, то сопряженный оператор А*, отображающий  в
в 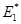 , также вполне непрерывен.
, также вполне непрерывен.
IX. Если А – линейный ограниченный оператор, множествозначений которого замкнуто, то для разрешимости уравнения А*f=  необходимо и достаточно чтобы
необходимо и достаточно чтобы  для всех x являющихся решением уравнения Ах=0.
для всех x являющихся решением уравнения Ах=0.
Х. Если L – подпространство банахова пространства Е и размерность пространства L конечна, то L имеет прямое дополнение в Е, т.е. Е=L+M, где М – подпространство пространства Е. При этом  .
.
Определения.
Пусть Е1 и Е2 – банаховы пространства, {Е1→Е2} – пространство линейных ограниченных операторов, действующих из Е1 в Е2.
Рассмотрим уравнение
Вх=0 , ВÎ{Е1→Е2}. (1.1)
Решения уравнения (1.1) называются нулями оператора В. Множество нулей оператора В называется ядром оператора В и обозначается ker B или N(B).
ker B = N(B)={x: Bx=0}.
Множество kerB линейно изамкнуто:
а) В(a1x1+a1x2)=a1Bx1+a2Bx2=0, если Вх1=0, Вх2=0, a1,a2 – комплексные постоянные;
в) если Вхn=0 и lim xn=x0, то
 .
.
Таким образом, ker B – подпространство банахова пространства Е1.
Число линейно независимых нулей оператора В, точнее – размерность подпространства ker B, называется первым дефектным числом оператора В и обозначается a=dim ker B.
Рассмотрим неоднородное уравнение:
Вх=y (1.2)
Оператор В, а вместе с ним и соответствующее ему уравнение (1.2) называется нормально разрешимым, если в пространстве  , сопряженном с Е2, существует (быть может, пустое) множество N*(B) функционалов
, сопряженном с Е2, существует (быть может, пустое) множество N*(B) функционалов  , таких, что для разрешимости уравнения (1.1) необходимо и достаточно, чтобы
, таких, что для разрешимости уравнения (1.1) необходимо и достаточно, чтобы  для всех
для всех  .
.
Множество N*(B) называют ядром оператора В и обозначают N*(B)=cokerB. Элементы множества N*(B) называют дефектными функционалами. Если N*(B) замкнуто, то оно будет подпространством пространства  , называемым дефектным подпространством оператора В. Его размерность обозначается так: dim coker B=b и называется вторым дефектным числом оператора В.
, называемым дефектным подпространством оператора В. Его размерность обозначается так: dim coker B=b и называется вторым дефектным числом оператора В.
Упорядоченная пара (a,b) чисел a и b называется дефектнойхарактеристикой, или коротко: d – характеристикой оператора В, а число æ=a-b - его индексом. Индекс определен, если хотя бы одно из чисел a и b конечно.
В дальнейшем мы иногда будем писать вместо æ, a и b соответственно æ(В), a(В) и b(В) для того, чтобы подчеркнуть, что эти величины относятся к оператору В.
Нормально разрешимый оператор ВÎ{Е1→Е2}, у которого оба дефектные числа конечны, называется оператором Нетера или Ф-оператором.
Если a конечно, b=¥, то соответствующий оператор ВÎ{Е1→Е2}, называется Ф+ - оператором. В этом случае в пространстве N(B) существует a-мерный базис х1,х2,…,хa
Если a=¥, b - конечно, то оператор называется Ф- оператором. В этом случае в пространстве N*(B) существует b-мерный базис z1,z2,…,zb.
Для нетерова оператора В общее решение однородного уравнения Вх=0 будет
 (ск – произвольные постоянные),
(ск – произвольные постоянные),
а условия разрешимости неоднородного Вх=y имеют вид
zj(y)=0 , j=1,2,…,b. (1.3)
Если a=b, то оператор называется квазифредгольмовым. Частным случаем квазифредгольмовых операторов являются операторы Фредгольма, т.е. операторы вида
В=I+T,
где Т – вполне непрерывный оператор, а I - единичный оператор. Простым примером оператора Фредгольма является интегральный оператор с непрерывным ядром К(s,t)
Bx=x+Tx , Tx= 
Как известно, он действует из пространства непрерывных на отрезке [a,b] функций С[a,b] и С[a,b], причем является вполне непрерывным оператором.
Название «оператор Нетера» имеет следующую историю. Теория сингулярных интегральных уравнений с ядром  впервые разрабатывалась в трудах Ф.Нетера. Основные теоремы этой теории носят его имя. Нормальные разрешимые операторы с конечной d-характеристикой являются естественным обобщением интегральных операторов с ядром
впервые разрабатывалась в трудах Ф.Нетера. Основные теоремы этой теории носят его имя. Нормальные разрешимые операторы с конечной d-характеристикой являются естественным обобщением интегральных операторов с ядром  , поэтому за ними и укрепилось название «операторы Нетера».
, поэтому за ними и укрепилось название «операторы Нетера».
Теория сингулярных интегральных уравнений с ядром Коши развивались в работах Т.
2. Разложения пространства Е1 и Е2 в прямые суммы.
Пусть В – оператор Нетера. Обозначим через  a - мерное подпространство нулей этого оператора. Возьмем в
a - мерное подпространство нулей этого оператора. Возьмем в  какие-либо базисные элементы х1, х2,…, хa, тогда в сопряженном с Е1 пространстве существует биортогональная система функционалов x1,x2,…,xa:
какие-либо базисные элементы х1, х2,…, хa, тогда в сопряженном с Е1 пространстве существует биортогональная система функционалов x1,x2,…,xa:
1 , j=I,

0, j¹i.
Положим
 (2.1)
(2.1)
Оператор Р – линейный, ограниченный в силу непрерывности функционалов xj(x). Очевидно, Рхк=хк, Р2х=Рх. Оператор Р называется оператором проектирования на подпространстве  или коротко проектором. Пусть х – любой элемент Е1. положим х′=Рх, х″=(I-P)x, тогда
или коротко проектором. Пусть х – любой элемент Е1. положим х′=Рх, х″=(I-P)x, тогда
Х=Рх+(х-Рх)=х′+х″. (2.2)
Таким образом,  . Элементы х″ аннулируются проектором Р. в самом деле
. Элементы х″ аннулируются проектором Р. в самом деле
Рх″=Р(х-Рх)=0 (2.3)
От сюда следует, что элементы х″ образуют ядро линейно ограниченного оператора Р: {х″}=кеr Р. следовательно, {х″} –замкнутое линейное многообразие, т.е. подпространство пространства Е1. обозначим это подпространство  . Из (2.1) и (2.2) следует, что элементы х″Î
. Из (2.1) и (2.2) следует, что элементы х″Î  аннулируются также и функционалами xj:
аннулируются также и функционалами xj:
xj(x″)=0 , j=1,2,…,a.
Представление (2.2) единственно, так как равенство х′+х″=0. В самом деле, так как х′Î  , то существует единственным образом определенные постоянные dk, такие, что
, то существует единственным образом определенные постоянные dk, такие, что  .При условии xк(х″)=0 получаем: dk=0, т.е. х″=0. Отсюда заключаем, что пространство Е1 разлагается в прямую сумму подпространств
.При условии xк(х″)=0 получаем: dk=0, т.е. х″=0. Отсюда заключаем, что пространство Е1 разлагается в прямую сумму подпространств  и
и  :
:
Е1=  +
+  .
.
Аналогичное разбиение проведем в пространстве Е2. За основу возьмем систему z1,z2,…,zb элементов пространства Е2, биортогональных дефектным функционалам z1,z2,…,zb, т.е. таких, что zj(zi)=dij.
Введем в Е2 проектор Qy на b - мерное подпространство  , базисом которого служат элементы zk, к=1,2,…, b, проложив
, базисом которого служат элементы zk, к=1,2,…, b, проложив
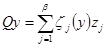 (2.4)
(2.4)
Произвольный элемент yÎ Е2 можно единственным образом представить в виде y=Qy+[y-Qy]=y′+y″, где y′=Qy, y″=(I-Q)y, множество {y″} обозначим  . Очевидно, Q y″==0. следовательно,
. Очевидно, Q y″==0. следовательно,  как ядро ограниченного оператора Q будет подпространством пространства Е2. В силу линейной независимости элементов zj на (2.4) вытекает, что zj(y″)=0 для всех j=1,2,…,b. Таким образом, подпространство
как ядро ограниченного оператора Q будет подпространством пространства Е2. В силу линейной независимости элементов zj на (2.4) вытекает, что zj(y″)=0 для всех j=1,2,…,b. Таким образом, подпространство  состоит из тех элементов y″Î Е2, для которых разрешимо уравнение Вх=у. Следовательно, пространство
состоит из тех элементов y″Î Е2, для которых разрешимо уравнение Вх=у. Следовательно, пространство  - это область значений или образ JmB оператора В. ясно, что при b=0 пространство
- это область значений или образ JmB оператора В. ясно, что при b=0 пространство  совпадает со пространством Е2 .
совпадает со пространством Е2 .
Так же, как и в случае пространства Е1, имеем представление пространства Е2 в виде прямой суммы:
Е2=  +
+  .
.
3. Сужение нетерова оператора В на  .
.
Если a=b=0, то уравнение Вх=у имеет единственное решение х=В-1у, где В-1 – обратный к В, ограниченный по теореме Банаха оператор.
Что будет в случае a+b>0 ? Тогда уравнение Вх=у или неразрешимо, или у него решение не единственное, т.е. обратного оператора на всем Е2 здесь не будет. Обозначим через  сужение оператора В на
сужение оператора В на  . Оператор
. Оператор  устанавливает между пространствами
устанавливает между пространствами  и
и  взаимно однозначное соответствие. В самом деле, каждому
взаимно однозначное соответствие. В самом деле, каждому  отвечает один элемент Вх″, принадлежащий
отвечает один элемент Вх″, принадлежащий  в силу того, что уравнение Вх=Вх″ разрешимо (оно имеет решение х=х″). Наоборот, уравнение Вх=у″ разрешимо при у″Î
в силу того, что уравнение Вх=Вх″ разрешимо (оно имеет решение х=х″). Наоборот, уравнение Вх=у″ разрешимо при у″Î  , и в
, и в  это решение единственно, ибо разность двух различных решений в
это решение единственно, ибо разность двух различных решений в должна одновременно принадлежать и
должна одновременно принадлежать и  и
и  ,что невозможно, если эта разность не нуль. По теореме Банаха, из взаимно однозначного соответствия между
,что невозможно, если эта разность не нуль. По теореме Банаха, из взаимно однозначного соответствия между  и
и  вытекает существование обратного ограниченного оператора
вытекает существование обратного ограниченного оператора  . Разумеется, в Е1 решение уравнения Вх=у при уÎ
. Разумеется, в Е1 решение уравнения Вх=у при уÎ  , a>0 будет не единственным:
, a>0 будет не единственным:
 (ск – произвольные постоянные)
(ск – произвольные постоянные)
4. Лемма Шмидта и теорема Никольского.
Прежде чем приступить к формулировке и доказательству одного важного свойства квазифредгольмовых операторов, покажем, что для интегрального уравнения Фредгольма добавлением интегрального слагаемого с вырожденным ядром можно всегда прийти к первому случаю альтернативы Фредгольма (разрешимость неоднородного уравнения при любой правой части и лишь нулевое решение у соответствующего однородного уравнения).
Итак, пусть для уравнения
 (4.1)
(4.1)
имеет место второй случай альтернативы Фредгольма, т.е. соответствующее ему однородное уравнение
 (4.2)
(4.2)
имеет a (a>0) линейно независимых решений.
Рассмотрим вспомогательное уравнение
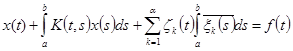 ; (4.3)
; (4.3)
содержащее неопределенные пока функции zк(t) и xк(s), которые подберем так, чтобы для уравнения (4.8) имел место первый случай альтернативы.
Запишем однородное уравнение, соответствующее уравнению (4.8), в виде
 (4.4)
(4.4)
и будем рассматривать как неоднородное со свободным членом

Если х(t) – какое-либо ненулевое решение уравнения (4.4), то должно выполняться условие ортогональности его правой части функциям zj(t), образующим базис решений однородного уравнения, сопряженного с уравнением (4.2). Напишем это условие в виде
 (4.5)
(4.5)
Выберем функции zk(t) так, чтобы выполнялись равенства
 .
.
При таком выборе функций zk(t) из (4.5) получим
 (4.6)
(4.6)
Если эти соотношения выполнены, то уравнение (4.4) совпадает с исходным однородным уравнением (4.2). Следовательно, 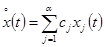 , где хj(t) – базис решений уравнения (4.2), сj – некоторые постоянные.
, где хj(t) – базис решений уравнения (4.2), сj – некоторые постоянные.
Подставляя полученное выражение для  в (4.5), будем иметь
в (4.5), будем иметь
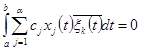 , к=1,2,…,a.
, к=1,2,…,a.
Если теперь выбрать функции xk(t) так, чтобы
 ,
,
то из предыдущего равенства будет вытекать, что сj=0, j=1,2,…, a, а это означает, чтоо и  =0.
=0.
Итак, для того, чтобы уравнение (4.4) не имело других решений, кроме нулевого, функции xk(t) и z k(t) должны быть биортогональными функциями хj(t) и zj(t) соответственно. Если хj(t) и zj(t) были ортонормированны, то проще всего взять
xk(t)= хк(t), z k(t)= zк(t).
Вспомогательное уравнение (4.3) при этом имеет вид
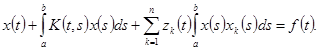
Заметим далее, что если исходное уравнение (4.1) при некоторой правой части f(t) разрешимо, т.е. выполнены условия
 , J=1,2,…, a (4.7)
, J=1,2,…, a (4.7)
то решение уравнения (4.3) при этой же правой части будет удовлетворять уравнению (4.1). В самом деле, выражение  , принадлежащее образу оператора
, принадлежащее образу оператора  , ортогонально функциям zj(t). Отсюда, в силу ортогональности системы функций хк(s), к=1, 2,…, a и равенства (4.3) вытекает, что
, ортогонально функциям zj(t). Отсюда, в силу ортогональности системы функций хк(s), к=1, 2,…, a и равенства (4.3) вытекает, что

Из этого равенства следует, что уравнение (4.8) совпадает с (4.1), что и утверждалось.
Сейчас мы сформулируем соответствующий результат для общих квазифредгольмовых операторов, обобщив конструкцию, использованную выше.
Лемма Шмидта. Пусть ВÎ{Е1®Е2} - квазифредгольмов оператор и

 ,
,
тогда:
1. Оператор 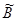 имеет ограниченный обратный: уравнение
имеет ограниченный обратный: уравнение 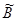 х = у единственным образом разрешимо в Е1 при любом у на Е2
х = у единственным образом разрешимо в Е1 при любом у на Е2
2. Если  , то решение уравнения
, то решение уравнения 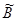 х = у совпадает с решением уравнения
х = у совпадает с решением уравнения  в подпространстве
в подпространстве  .
.
3. Если  , то решение уравнения
, то решение уравнения 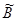 х = у совпадает с решением уравнения Rx=y и в подпространстве
х = у совпадает с решением уравнения Rx=y и в подпространстве  .
.
Доказательство. Запишем уравнение 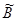 х = у в виде системы:
х = у в виде системы:
 , к=1, 2,…, a.
, к=1, 2,…, a.
Условия разрешимости первого уравнения этой системы имеют вид
 , m=1, 2,…, a.
, m=1, 2,…, a.
Учитывая биортогональность элементов {zk} функционалам {zк}, заключаем, что  . Следовательно, первое из уравнений (4.8) примет вид:
. Следовательно, первое из уравнений (4.8) примет вид:
 .
.
Будем решать это уравнение в пространстве Е1, тогда

Распорядимся постоянными dk так, чтобы удовлетворить соотношениям Сm=xm(х)
 .
.
Так как  , а на таких элементах функционалы xm исчезают, то dm=zm(y).
, а на таких элементах функционалы xm исчезают, то dm=zm(y).
Итак,
 (4.9)
(4.9)
Первое утверждение леммы Шмидта доказано.
Пусть теперь  , тогда zк(y)=0 в формуле (4.9) и
, тогда zк(y)=0 в формуле (4.9) и  . Первое из этих равенств следует из определения пространства
. Первое из этих равенств следует из определения пространства  , а второе из первого проектора Q:
, а второе из первого проектора Q:
 .
.
От сюда вытекает искомое равенство  , что и завершает доказательство леммы Шмидта.
, что и завершает доказательство леммы Шмидта.
Выводы: 1) Из первой части леммы Шмидта вытекает, что
 ,
,
т.е. квазифредгольмов оператор В представим в виде суммы обратимого оператора 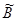 и конечномерного (проектора
и конечномерного (проектора  ).
).
2) Из второй части леммы Шмидта следует, что оператор 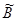 является расширением оператора
является расширением оператора  из пространства
из пространства  на новое пространство Е1.
на новое пространство Е1.
3.) Оператор 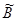 устанавливает взаимно однозначное соответствие между базисом {хк} нулей оператора В и элементами {zk} биортогональными дефектным функционалам {zк}. В самом деле,
устанавливает взаимно однозначное соответствие между базисом {хк} нулей оператора В и элементами {zk} биортогональными дефектным функционалам {zк}. В самом деле,

так как zi-Qzi=zi-zi=0.
Замечание. Рольслагаемого  , входящего в оператор
, входящего в оператор 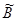 , такова: если
, такова: если 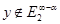 , то естественно ввести свободный член уравнения в пространство
, то естественно ввести свободный член уравнения в пространство  , т.е. некоторую линейную комбинацию элементов z.k. Коэффициенты этой линейной комбинации, являющиеся функционалами, действующими на искомый элемент х, подбираются так, чтобы полученное однородное уравнение имело лишь тривиальное решение. Подобные рассуждения часто применяются при исследовании разрешимости различных функциональных уравнений.
, т.е. некоторую линейную комбинацию элементов z.k. Коэффициенты этой линейной комбинации, являющиеся функционалами, действующими на искомый элемент х, подбираются так, чтобы полученное однородное уравнение имело лишь тривиальное решение. Подобные рассуждения часто применяются при исследовании разрешимости различных функциональных уравнений.
Теорема С. М. Никольского. Для того, чтобы оператор ВÎ{Е1®Е2} был квазифредгольмовым оператором, необходимо и достаточно выполнение одного из следующих условий:
а) B=A+V, где А имеет ограниченный обратный А-1, а V – вполне непрерывный;
б) В=А1+V1, где А1 имеет ограниченный обратный 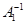 , а V1 – конечномерный;
, а V1 – конечномерный;
Доказательство. Необходимость следует из леммы Шмидта с учетом того, что конечномерный оператор вполне непрерывный. Достаточность следует доказывать только в предположении а), т.к. конечномерный оператор, фигурирующий в б), вполне непрерывен.
Имеем: уравнение Вх=у эквивалентно уравнению А-1Вх=А-1у, иными словами,
 .
.
Но А-1V=U – вполне непрерывный оператор как композиция ограниченного А-1 и вполне непрерывного V, а для уравнений вида

с вполне непрерывным оператором U справедлива теория Фредгольма.
Характеристические операторы
В теории сингулярных интегральных уравнений с ядром Коши важную роль играют так называемые характеристические сингулярные операторы
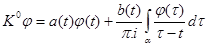 ,
, 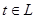
(  - гладкий, простой, замкнутый контур;
- гладкий, простой, замкнутый контур;  ,
,  - заданные функции, удовлетворяющие условию
- заданные функции, удовлетворяющие условию  ).
).
В зависимости от коэффициентов  и
и  индекс æ оператора
индекс æ оператора  может быть положительным, нулевым или отрицательным, а
может быть положительным, нулевым или отрицательным, а 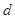 - характеристика этого оператора может иметь лишь три формы:
- характеристика этого оператора может иметь лишь три формы:
1)  - в случае
- в случае  ,
,
2) (0,0) - в случае 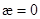 ,
,
3) 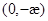 - случае
- случае  .
.
Многие вопросы теории сингулярных уравнений с ядром Коши решаются при помощи выделения на полного сингулярного оператороа его характеристической части.
Естественно обобщить эту операцию на случай произвольного оператора Нетера  .
.
Пусть 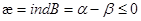 . Покажем, что оператор
. Покажем, что оператор  можно представить в виде
можно представить в виде
 ,
,
где 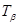 - конечномерный оператор, оператор Нетера
- конечномерный оператор, оператор Нетера 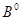 имеет
имеет 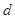 - характеристику вида
- характеристику вида 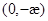 .
.
Воспользуемся конструкцией из леммы Шмидта
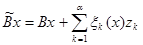 . (11.2)
. (11.2)
Ясно, что индекс оператора 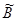 равен
равен  , так как
, так как 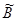 отличается от
отличается от  на конечномерный оператор. Мы покажем, что оператор
на конечномерный оператор. Мы покажем, что оператор 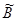 не имеет других нулей, кроме тривиального.
не имеет других нулей, кроме тривиального.
Отсюда будет следовать, что его 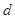 - характеристика имеет вид
- характеристика имеет вид 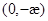 . Таким образом, из (11.2) получим представление(11.1) при
. Таким образом, из (11.2) получим представление(11.1) при  и
и  .
.
Обращаем внимание на то, что суммирование ведется в пределах от 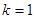 до
до 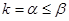 по числу функционалов
по числу функционалов  . Число элементов
. Число элементов  равно
равно  , следовательно, элементов
, следовательно, элементов  хватит для образования суммы
хватит для образования суммы 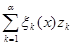 .
.
Пусть 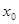 - какое-либо решение уравнения
- какое-либо решение уравнения  . Так как
. Так как  , то
, то 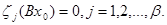 Учитывая это, положим в (11.2)
Учитывая это, положим в (11.2) 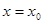 и применим к обеим частям полученного равенства функционалы
и применим к обеим частям полученного равенства функционалы 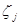 . В результате получим
. В результате получим
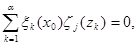
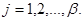
Отсюда, ограничиваясь значениями 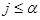 и учитывая равенства
и учитывая равенства  , получаем
, получаем  для
для 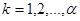 . Это означает, что
. Это означает, что 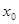 является решением уравнения
является решением уравнения 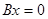 , т.е.
, т.е.  . Из равенств
. Из равенств  вытекает, что все
вытекает, что все 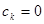 , т.е.
, т.е. 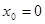 , что и требовалось доказать.
, что и требовалось доказать.
Пусть  . Покажем, что имеет место представление (11.1), где
. Покажем, что имеет место представление (11.1), где 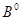 имеет
имеет 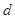 - характеристику вида
- характеристику вида  .
.
Положим
 (11.3)
(11.3)
(на этот раз  , поэтому суммирование ведется лишь до
, поэтому суммирование ведется лишь до  )
)
Ясно, что 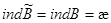 и нам достаточно показать, что
и нам достаточно показать, что  . Рассмотрим уравнение
. Рассмотрим уравнение  , т.е.
, т.е.
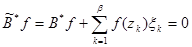 . (11.4)
. (11.4)
Аналогично предыдущему легко показать, что у этого уравнения нет решений, кроме нулевого. В самом деле, 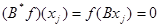 . Следовательно, если
. Следовательно, если  - какое-либо решение уравнения (11.4), то
- какое-либо решение уравнения (11.4), то  ,
, 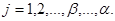
Учитывая равенства 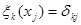 , получаем, что
, получаем, что 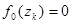 . Соотношение (11.4) при
. Соотношение (11.4) при  обращается в
обращается в  и, следовательно,
и, следовательно,  , где
, где  - произвольные постоянные, а
- произвольные постоянные, а  дефектные функционалы оператора
дефектные функционалы оператора  . Подставляя полученное выражение в равенство
. Подставляя полученное выражение в равенство 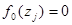 , будем иметь
, будем иметь  ,
, 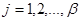 .
.
Учитывая равенства  , заключаем, что
, заключаем, что 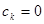 , а
, а 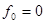 , что и требовалось доказать. Итак,
, что и требовалось доказать. Итак,  , а так как
, а так как 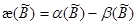 , то
, то 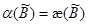 и
и  .
.
Таким образом, оператор  представим в виде (11.1) при
представим в виде (11.1) при  и
и  .
.
Ясно, что определение характеристической части оператора в указанном выше смысле не будет однозначным.
Замечание. Рассмотрим совокупность операторов вида  , где
, где  - фиксированный оператор Нетера, имеющий положительный индекс
- фиксированный оператор Нетера, имеющий положительный индекс 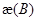 , а
, а 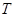 пробегает всевозможные вполне непрерывные операторы. Как мы знаем
пробегает всевозможные вполне непрерывные операторы. Как мы знаем  и, следовательно,
и, следовательно, 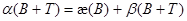 .
.
Отсюда число нулей каждого из операторов  не меньше, чем
не меньше, чем 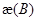 . Минимально возможное число нулей равно
. Минимально возможное число нулей равно 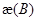 , и оно действительно достигается при
, и оно действительно достигается при  .
.
В терминах характеристической части оператора удобно формулировать теоремы о возмущении нетеровых операторов. Одна из таких теорем приводится ниже.
Пусть 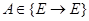 - оператор Нетера,
- оператор Нетера, 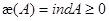 ,
,  , где
, где  - характеристическая часть оператора
- характеристическая часть оператора 
 ,
,  - вполне непрерывный оператор. Через
- вполне непрерывный оператор. Через 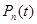 обозначим многочлен от
обозначим многочлен от 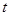 степени
степени 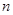 с постоянными коэффициентами.
с постоянными коэффициентами.
Теорема 1.11. Пусть оператор  удовлетворяет условию
удовлетворяет условию  , где
, где  - некоторый вполне непрерывный оператор. Тогда оператор
- некоторый вполне непрерывный оператор. Тогда оператор  при всех постоянных значениях
при всех постоянных значениях  , таких, что
, таких, что  является оператором нетера и
является оператором нетера и  .
.
Доказательство. При выполнении условий  и
и  оператор
оператор  имеет нулевой индекс. Следовательно, по теореме Никольского он представим в виде
имеет нулевой индекс. Следовательно, по теореме Никольского он представим в виде  , где
, где  - обратимый, а
- обратимый, а 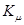 - вполне непрерывный операторы, действующие в пространстве
- вполне непрерывный операторы, действующие в пространстве 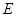 .
.
Легко убедиться непосредственной проверкой, что оператор  можно представить в виде (см. § 10, формула 10.5)
можно представить в виде (см. § 10, формула 10.5)
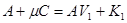 , (11.5)
, (11.5)
где 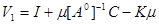 - обратимый оператор, а
- обратимый оператор, а 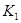 определяется равенством
определяется равенством
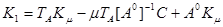 . (11.6)
. (11.6)
Так как 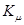 и
и  вполне непрерывны, то
вполне непрерывны, то 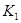 - вполне непрерывный оператор, следовательно, по теореме 5.10 из представления (11.5) вытекает, что
- вполне непрерывный оператор, следовательно, по теореме 5.10 из представления (11.5) вытекает, что  - оператор Нетера и
- оператор Нетера и  . Теорема 1.11 доказана Е.А. Ивановым.
. Теорема 1.11 доказана Е.А. Ивановым.
Примеры линейных операторов
- Нуль- оператор определяется равенством
 ,
,  .
.
Очевидно  и
и  может быть как конечны, так и бесконечным в зависимости от того, конечномерно или бесконечномерно пространство
может быть как конечны, так и бесконечным в зависимости от того, конечномерно или бесконечномерно пространство  . Для определения
. Для определения  учтем, что уравнение
учтем, что уравнение  разрешимо лишь при
разрешимо лишь при  . Поэтому
. Поэтому  , если и
, если и 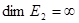 и
и  , если
, если  . Таким образом, при различных предположениях относительно размерности пространств
. Таким образом, при различных предположениях относительно размерности пространств  и
и  нуль оператор может оказаться как оператором Нетера, так и
нуль оператор может оказаться как оператором Нетера, так и  - оператором; также возможен случай, когда оба числа
- оператором; также возможен случай, когда оба числа  и
и  бесконечны.
бесконечны.
- Единичный оператор
 определен, если
определен, если  . Ясно, что
. Ясно, что  при
при
любом выборе пространства  , т.е.
, т.е.  . Второе дефектное число зависит от того, каково пространство
. Второе дефектное число зависит от того, каково пространство  . Если
. Если  , то
, то  и оператор обратим. Если же
и оператор обратим. Если же  , то
, то 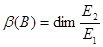 и могут иметь место различные случаи. Пусть, например,
и могут иметь место различные случаи. Пусть, например,  - пространство комплекснозначных функций
- пространство комплекснозначных функций  точек
точек 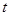 единичной окружности
единичной окружности  с суммируемым квадратом, а
с суммируемым квадратом, а  - подпространство
- подпространство  , состоящее из функций
, состоящее из функций  таких, что
таких, что
 ,
, 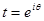 .
.
Тогда для того, чтобы функция  из
из  принадлежала образу оператора
принадлежала образу оператора  , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
 .
.
В этом случае  и
и  - оператор Нетера
- оператор Нетера
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...