Условия принадлежности линейного оператора классу операторов Нетера.

Вернемся к рассмотрению операторов Нетера. Обобщением теоремы Никольского является следующее утверждение, содержащее необходимое и достаточное условие принадлежности оператора классу операторов Нетера.

Теорема 1.7. первая теорема Аткинсона.

Для того, чтобы оператор ВÎ{Е₁®Е₂} был оператором Нетера, необходимо и достаточно, чтобы существовали:

а) линейный оператор UÎ{ Е₂® Е₁},

б) конечномерные операторы К₁Î{ Е₁® Е₁} и К₂Î{ Е₂® Е₂} такие, что

UB=I+ К₁, BU= I+ К₂. (7.1)

Доказательство. Необходимость. Покажем, что если S – оператор Нетера с d – характеристикой (a,b), то имеют место предположения (7.1), при

на ,

U= К₁=-Р, К₂=-Q,

0 на ,

где Р и Q соответственно a и b - мерные проекторы вида (2.1) и (2.4), а - сужение В на .

Действительно, если хÎЕ₁, то

UBx= Bx= B(P+I-P)x= B(I-P)x=(I-P)x,

а если уÎЕ₂,то

Buy=BU(Q+I-Q)y=B (I-Q)y=(I-Q)y.

В первой строке ВР=0, B=I на элементах из . Во второй строке BUQy=0, так как QyÎ и B =I на элементах (I-Q)y, принадлежащих пространству . Достаточность будет доказана ниже при доказательстве второй теоремы Аткинсона.

Теорема 2.7. вторая теорема Аткинсона.

Для того, чтобы оператор ВÎ{Е₁®Е₂} был нетеровым, необходимо и достаточно, чтобы существовали линейные операторы UÎ{ Е₂® Е₁} и VÎ{ Е₂® Е₁} такие, что UB и BV – нетеровы операторы.

Доказательство. Необходимость условий теоремы вытекает из доказанной выше необходимости условий первой теоремы Аткинсона. Докажем их достаточность. Сперва установим, что числа a и b у оператора В конечны. Рассмотрим уравнение UBx=0. каждый нуль оператора В является нулем UB, т.е. ker BÌker UB. Так как dimker UB – конечная величина, ибо UB – оператор Нетера, то конечной будет и величина dimker B.

Учтем теперь, что BV – оператор Нетера. Разложим пространство Е₂ в прямую сумму:

,

где b(BV) – размерность коядра нетерова оператора BV; 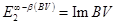. Имеют место вложения:

.

Поэтому справедливо неравенство

,

т.е. b(B)£ b(BV). Итак, оператор В имеет конечную d-характеристику. Остается показать, что множество ImB значений оператора В замкнуто. С этой целью представим пространство Е₁ в виде прямой суммы

подпространств =ker B и .

Покажем сначала, что выполняется неравенство

, (7.2)

из которого затем выводом замкнутости образа оператора В. Если указанное неравенство не выполняется, то найдется такая последовательность , чтоо . Действительно, для каждого n в этом случае найдется такое , что . Можно считать, что ||x_n||=1, n=1,2,…В самом деле, , следовательно, , где , причем .Учтем теперь, что оператору UB как нетерову отвечает такой оператор W, что WUB=I+T₁, где Т₁ – конечномерный, а значит, и вполне непрерывный. Так как последовательность ограничена, то существует такая ее подпоследовательность (опять назовем ее ), что Т₁ сходится к некоторому элементу ÎЕ₁. Так как WUB ®0, то из равенства WUB = + Т₁ следует, что (-æ)Î . Так как , то Î . Но у подпространства и единственный общий элемент-ноль, следовательно, =0, что противоречит соотношениям ||x_n||=1 и х=lim x_n.

Из неравенства (7.2) вытекает, что если имеется последовательность у_n=Вх_n, х_nÎ такая, что существует , то для достаточно больших m и n

.

Отсюда вытекает существование предела , принадлежащего пространству Е₁ в силу его полноты.

В результате получаем возможность сделать предельный переход в равенстве у_n=Вх_n, что дает , а это и требовалось доказать. Вторая теорема Аткинсона полностью доказана.

Из доказанной достаточности условий второй теоремы Аткинсона очевидно вытекает и достаточность условий первой теоремы Аткинсона.

Следствие. Если В – оператор Нетера, то и В^* – оператор Нетера, причем æ(В^*)=-æ(В). В самом деле, переходя в равенствах (7.1) к сопряженным оператора, получим

.

Так как операторы и вполне непрерывны, а оператор U^* – ограниченный, то по второй теореме Аткинсона (достаточность) В^* – оператор Нетера.

Покажем, что æ(В^*)=-æ(В). с этой целью рассмотрим уравнение (В^*f)=g, где . Для любого х из Е₁ имеем: (В^*f)х=g(х) или f(Bx)=g(x). Последнее равенство определяет искомый функционал f на элементах подпространства Im B= , т.е. на одном из слагаемых прямой суммы, в которую разлагается пространство Е₂:

Е₂= + .

Ниже будет показано, что значения f на элементах подпространства можно задавать произвольно. Возьмем далее и положим у=Qy+(I-Q)y. Тогда (I-Q)yÎ , а . Отсюда f(y)=f[(I-Q)y]+f(Qy)=f[(I-Q)y]+ . Первое слагаемое в этом равенстве определить, так как (I+Q)yÎIm B, а именно f[(I-Q)y]=g(x), где х – решение уравнения Вх=(I-Q)y, имеющее вид:

.

Здесь {x_k} – базис ядра оператора В, (определение оператора см. в §3). Таким образом, решение уравнения В^*f=g имеет вид

.

Для непрерывности функционала f(y) необходимо и достаточно, чтобы g(x_k)=0, k=1,2,…,a. В самом деле, лишь при выполнении этого условия f(y)®0 при ||y||®0. Отсюда заключаем, что b(В^*)=a(В). Далее имеем

. (7.3)

Так как , то функционал f, определенный формулой (7.3), будет решением уравнения ^B*f=g при произвольных значениях f(z_j). Следовательно, a(В^*)= b(В). таким образом, æ(В^*)=a (В^*)-b(В^*)=b(В)- a(В)=- æ(В), что и требовалось доказатьь.

При доказательстве второй теоремы Аткинсона мы воспользовались тем фактом, что оценка (7.2) позволяет сделать вывод о замкнутости образа оператора В.

Можно доказать более сильное утверждение.

Теорема 3.7. Пусть ВÎ{Е₁®Е₂} и

, где КÎ{Е₁®Е₂} - некоторый вполне непрерывный оператор. Тогда ядро оператора В конечномерно, а его образ замкнут.

Доказательство. 1. Покажем, что из любой последовательности решений однородного уравнения Вх=0 можно выделить сходящуюся подпоследовательность. Это будет означать, что единичный шар в подпространстве компактен, что может быть лишь в случае, когда - конечномерно. Указанным свойством обладает подпоследовательность такая, что последовательность имеет предел. В самом деле, учитывая, что В =0, получим из условия теоремы

Отсюда следует, что подпоследовательность сходящаяся, что и требовалось установить.

2. Для доказательства замкнутости образа оператора В рассмотрим подпоследовательность

у_nÎIm B, имеющую предел . Для каждого у_n найдем такое решение х_n уравнения Вх=у_n, норма которого минимальна. Такое решение существует, так как ядро оператора В конечномерно.

3. Покажем, что последовательность {x_n} ограничена в Е₁. предположим противное. Тогда существует такая подпоследовательность , что . Так как последовательность 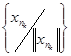ограниченная, то можно построить такую ее подпоследовательность, что будет существовать предел . Для любых двух членов этой последовательности и , будет выполняться неравенство

. (7.4)

Так как последовательность {||y_n||} ограниченная, то из (7.4) следует, что последовательность 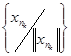фундаментальна в Е₁ и имеет предел . Из равенства 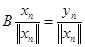заключаем, что В =0. переходя в (7.4) к пределу при m_k®¥ и учитывая, что , получим

.

Значит, существует такое число N, что

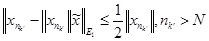. (7.5)

Имеем , а это в силу (7.5) противоречит минимальности .

4. Так как последовательность {x_n} ограниченная, то, разрежая, если нужно, эту последовательность, можно добиться сходимости последовательности (избегая усложнения записи мы не вводим новых обозначений для элементов разреженной последовательности S). Из (7.3) получим для произвольных и оценку

. (7.6)

Учитывая сходимость последовательности {y_n} из(7.6), заключаем, что последовательность фундаментальная. В силу полноты пространства Е₁ отсюда следует, что существует . Следовательно, в равенстве можно переходить к пределу при . Сделав этот предельный переход, получаем равенство . Таким образом, элемент , определенный как предел последовательности элементов у_n, принадлежащих образу оператора В, сам принадлежит образу оператора В. отсюда вытекает, что Im B – замкнутое множество.

Теорема доказана.

8. Регуляризация операторов.

Пусть ВÎ{Е₁®Е₂}. Ограниченный оператор R₁Î{Е₁®Е₂} такой, что R₁B=I+

T₁, где Т₁Î{Е₁®Е₁} - вполне непрерывный оператор, называется левым регуляризатором оператора В. аналогично вводится понятие о правом регуляризаторе, т.е. таком ограниченном операторе R_nÎ{Е₂®Е₁}, что BR_n=I+T₂, где Т₂Î{Е₂®Е₂} - вполне непрерывный оператор.

Замечание 1. Если оператор допускает левую регуляризацию, то он, очевидно, имеет не более конечного числа нулей. В самом деле, все нули исходного оператора будут нулями регуляризованного, т.е. ker BÌker R_лB. Отсюда вытекает, что dim ker B≤dim ker R_лB<¥, так как R_лB – оператор Фредгольма, размерность ядра которого, как известно, конечна.

Замечание 2. Если R_лÎ{Е₂®Е₁} - левый регуляризатор оператора В и оператор Î{Е₂®Е₁} - вполне непрерывный, то R_л+ также будет левым регуляризатором оператора В. Аналогичное утверждение справедливо и для правого регуляризатора.

Теорема 1.8. Если у ограниченного оператора ВÎ{Е₁®Е₂} есть левый регуляризатор R_лÎ{Е₂®Е₁} и правый регуляризатор R_пÎ{Е₂®Е₁}, то R_л будет также правым регуляризатором оператора В, а R_л – его левым регуляризатором.

Доказательство. По определению регуляризаторов имеем равенства

R_лB=I+T₁ , T₁Î{Е₁®Е₁},

ВR_п=I+T₂ , T₂Î{Е₂®Е₂},

Где Т₁ и Т₂ – вполне непрерывные операторы.

Умножая первое из полученных равенств справа на R_п, а второе – слева на R_л и вычитая из первого соотношения второе получим

.

Отсюда заключаем, что .

Операторы T₁R_пÎ{Е₂®Е₁} и R_лT₂Î{Е₂®Е₁} - вполне непрерывные как композиции вполне непрерывных и ограниченных, следовательно, R_п=R_л+T₃, где Т₃ - вполне непрерывный оператор. Поэтому R_п будет также левым регуляризатором, а R_л – правым. Заметим еще, что из условий теоремы вытекает, что В – оператор Нетера.

Следствие. Любой регуляризатор оператора Нетера – также оператор Нетера.

В самом деле, если R – левый (правый) регуляризатор нетерова оператора В, то R также будет и правым (левым) регуляризатором этого оператора, так как у В по первой теореме Аткинсона заведомо есть еще правый (левый) регуляризатор. Отсюда получаем

RB=I+T₁ , T₁Î{Е₁®Е₁},

BR=I+T₂ , T₂Î{Е₂®Е₂},

Где Т₁ и Т₂ – вполне непрерывные операторы. Отсюда видно, что В можно рассматривать как левый и правый регуляризатор оператора R. Существование левого и правого регуляризатора у оператора R обеспечивает по второй теореме Аткинсона его нетеровость.

Теорема 2.8. Если оператор ВÎ{Е₁®Е₂} допускает левую регуляризацию, то он нормально разрешим.

С. Г. Михлин доказал эту теорему для линейных замкнутых операторов. Для ограниченных операторов В доказательство этой теоремы содержится в приведенном выше доказательстве достаточности условий второй теоремы Аткинсона, причем это доказательство можно приспособить и к более общему случаю замкнутого оператора.

§9. Свойства операторов Нетера.

Теорема 1.9. (Теорема Аткинсона о композиции операторов Нетера).

Если ВÎ{Е₁®Е₂}, АÎ{Е₂®Е₃} - операторы Нетера, то оператор АВÎ{Е₁®Е₃} также оператор Нетера, причем

æ(АВ)=æ(А)+æ(В),

где

æ(А)=int A, æ(B)=int B, æ(AB)=int AB.

Доказательство. Покажем сначала, что АВ – оператор Нетера. По первой теореме Аткинсона (обозначения ясны из текста) имеем:

.

Тогда

,

Операторы и , по свойству композиции ограниченных операторов, из которых один является конечномерным, будут конечномерными, а тогда по первой теореме Аткинсона (достаточность) оператор будет оператором Нетера.

Определим теперь æ .

Для подсчета обозначим через -базис нулей оператора , а базис нулей оператора через . Из уравнения получаем:

, где - некоторые постоянные. Если таковы, что это уравнение разрешимо, то его решение будет решением исходного уравнения. Следовательно, для отыскания всех решений уравнения надо подобрать постоянные так, чтобы уравнение

(9.1)

оказалось разрешенным. Условия разрешимости уравнения (9.1), если принять за дефектные функционалы оператора элементы базиса ядра оператора , имеют вид:

,

, ,

Если , то линейно-независимых решений у системы (9.2) будет .

Отсюда

, (9.3)

где -произвольные постоянные, -линейные комбинации элементов , они, очевидно, линейно-независимые. Из (9.8) получаем

,

где - решение уравнения , 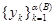- базис нулей оператора , -произвольные постоянные. Отсюда можно заключить, что , если будет показано, что система функций 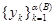линейно-независима. Это легко доказать методом от противого. Пусть

и не все равны нулю. Если при этом все , то получится, что линейно-независимыми будут 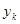, что невозможно. Если же хотя бы одно из отлично от нуля, например , то неоднородное уравнение (9.3) будет иметь своим решением нулевой элемент, что также невозможно.

Подсчитаем теперь . Рассмотрим уравнение

и применим к нему предыдущие рассуждения. Тогда получим

, причем постоянные следует выбирать так, чтобы это уравнение было разрешимо.

Из теоремы следует, что условие, необходимое и достаточное для разрешимости полученного уравнения, состоит в выполнении равенств

Эта система является транспонированной к системе (9.2), следовательно, ранг её матрицы также равен ; повторяя предыдущие рассуждения, получим

.

Отсюда следует, что

т.е. , что и требовалось.

Следствие. Индекс регуляризатора (левого и правого) оператора Нетера обратен по знаку индексу .

В самом деле, регуляризатор оператора Нетера сам является оператором Нетера, поэтому к выражениям

,

применима только что доказанная теорема. Учитывая, что индекс операторов Фредгольма и равен нулю, получаем требуемое.

Покажем, что свойство æ является характерным для индекса в том смысле, что любой функционал, обладающий этим свойством, при выполнении некоторых условий лишь целым постоянным множителем отличается от индекса. С этой целью рассмотрим множество операторов Нетера 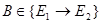, удовлетворяющее следующим условиям:

а) если , то и ;

б) если и -любой вполне-непрерывный оператор, то ;

в) существует такой оператор , что ;

г) если оператор , то его регуляризатор также принадлежит .

Теорема 2.9. Пусть функционал 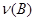, определенный на множестве операторов , удовлетворяет следующим условиям:

. Значения 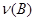- целые положительные или отрицательные числа или ноль.

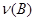. Функционал непрерывен на .

. Если , то .

. Если и имеет ограниченный обратный оператор , то . При этих условиях имеет место равенство 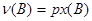, где -индекс оператора ,

а - целое число.

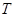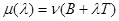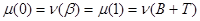Доказательство. Докажем сначала, что функционал не меняется, если к добавить вполне непрерывный оператор . В самом деле, и по выражение будет целозначной непрерывной функцией . Отсюда следует: , что и утверждалось.

Теперь докажем следующее свойство функционала : Если , то и . Действительно, если , то по теории Никольского , где -обратимый, а -вполне непрерывный операторы.

Следовательно, по .

Переходим к доказательству соотношения .

Возьмем произвольный оператор . Пусть Учитывая равенства ( - регуляризатор оператора ), заключаем, что . Отсюда из доказанного выше вытекает, что , следовательно, по , . Для вычисления значения заметим, что , где - вполне непрерывный оператор. Следовательно, , так как ,то . Следовательно, , где ,что и требовалось. Если же , то 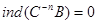и, следовательно, , т.е. и снова . Теорема доказана полностью.

Теорема 3.9. Если любые два из трех операторов , нетеровы, то и третий оператор нетеров, причем .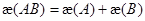

Доказательство. В случае, когда и - операторы Нетера, теорема доказана выше.

Пусть и - операторы Нетера. Обозначим через регуляризатор оператора и применим к равенству слева, что приводит к соотношению

, (9.4.)

в котором 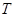- вполне непрерывный оператор. Из (9.4) заключаем, что оператор представим в виде

. (9.5)

Так как - операторы Нетера и - вполне непрерывный оператор, то из (9.5) следует, что и - оператор Нетера. Воспользовавшись второй частью теоремы 1.9, из равенства

получаем

.

Аналогичным образом доказывается теорема и в случае, когда и - операторы Нетера.