
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Эквивалентная регуляризация операторов
Введем следующие определения. Левый регуляризатор 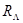 называеся левым эквивалентным, если уравнения
называеся левым эквивалентным, если уравнения  и
и  эквивалентны, т.е. каждое решение одного является в то же время решением другого.
эквивалентны, т.е. каждое решение одного является в то же время решением другого.
Правый регуляризатор  называется првым эквивалентным, если уравнения
называется првым эквивалентным, если уравнения  и
и  однозначно разрешимы или неразрешимы, причем в первом случае любое решение уравнения
однозначно разрешимы или неразрешимы, причем в первом случае любое решение уравнения  ,
,  представимо в виде
представимо в виде 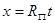 . Это означает, что уравнение
. Это означает, что уравнение 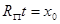 разрешимо для всех
разрешимо для всех  , так как любой такой элемент
, так как любой такой элемент 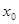 является решением уравнения
является решением уравнения  ,
,  .
.
Таким образом, в случае правой эквивалентной регуляризация не может произойти ни потери решений, ни приобретения новых решений, так как каждое решение регуляризованного уравнения  порождает решение
порождает решение  исходного уравнения
исходного уравнения
 , и наоборот, если
, и наоборот, если  - решение уравнения
- решение уравнения  , то
, то 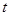 , найденное из уравнения
, найденное из уравнения  , будет удовлетворять уравнению
, будет удовлетворять уравнению  .
.
Теорема 1.13. (об эквивалентной регуляризации).
Если  - оператор Нетера, то его всегда можно эквивалентно регуляризировать: слева, если
- оператор Нетера, то его всегда можно эквивалентно регуляризировать: слева, если  , и справа, если
, и справа, если  .
.
Доказательство. При  применим к
применим к  слева какой- либо регуляризатор
слева какой- либо регуляризатор  , так что
, так что
 , (13.1)
, (13.1)
где  - вполне непрерывный оператор. Заметим, что
- вполне непрерывный оператор. Заметим, что  . Воспользовавшись формулой (11.1), представим
. Воспользовавшись формулой (11.1), представим  в виде
в виде
 (13.2)
(13.2)
где  имеет
имеет 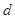 - характеристику
- характеристику  , а
, а  - вполне непрерывный оператор.
- вполне непрерывный оператор.
Из (13.1) и(13.2) получим
 .
.
Оператор  - вполне непрерывный и поэтому
- вполне непрерывный и поэтому  - левый регуляризатор оператора
- левый регуляризатор оператора  , а так как уравнение
, а так как уравнение  не имеет решений, отличных от нулевого, то регуляризация.
не имеет решений, отличных от нулевого, то регуляризация.
Если  , то применим к оператору
, то применим к оператору  справа какой-либо его регуляризатор
справа какой-либо его регуляризатор  :
:
 .
.
В данном случае  . Опять будем исходить из представления
. Опять будем исходить из представления
 ,
,
где  имеет
имеет 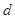 - характеристику
- характеристику  , а
, а  - вполне непрерывный оператор. Имеем
- вполне непрерывный оператор. Имеем
 .
.
Так как  - вполне непрерывный оператор, то
- вполне непрерывный оператор, то  -левый регуляризатор оператора
-левый регуляризатор оператора  . Уравнение
. Уравнение  разрешимо при любом
разрешимо при любом  , так как
, так как  имеет
имеет 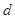 - характеристику
- характеристику  . Следовательно, по определению,
. Следовательно, по определению,  эквивалентный регуляризатор.
эквивалентный регуляризатор.
Отметим следующее важное обстоятельство. В случае положительного индекса после левой равносильной регуляризации получается уравнение с оператором, ядро которого совпадает с ядром исходного оператора ( соответствующие однородные уравнения имеют одни и те же решения). В случае же отрицательного индекса ( при правой эквивалентной регуляризации) это не так. А именно,  , где
, где  - любой правый равносильный регуляризатор. Для доказательства вспомним (см. доказательство теоремы о композиции операторов Нетера), что число нулей оператора
- любой правый равносильный регуляризатор. Для доказательства вспомним (см. доказательство теоремы о композиции операторов Нетера), что число нулей оператора  равно
равно  , где
, где  , следовательно,
, следовательно,  , так как
, так как  и
и  , что и требовалось доказать.
, что и требовалось доказать.
Следующее утверждение часто используется на практике при установлении эквивалентности уравнений.
Лемма. Пусть  - ограниченный оператор. Для того, чтобы уравнения
- ограниченный оператор. Для того, чтобы уравнения  и
и  были эквивалентны при любом свободном члене
были эквивалентны при любом свободном члене  , необходимо и достаточно, чтобы оператор
, необходимо и достаточно, чтобы оператор  не имел других нулей, кроме тривиального
не имел других нулей, кроме тривиального  .
.
Доказательство. Начнем с достаточности. Любое решение уравнения  удовлетворяет и уравнению
удовлетворяет и уравнению  , и наоборот, если
, и наоборот, если  - решение уравнения
- решение уравнения  , т.е.
, т.е.  , то
, то  .
.
Необходимость докажем так. Пусть  . Уравнения
. Уравнения  и
и  по предположению эквивалентны, причем второе уравнение сводится к однородному
по предположению эквивалентны, причем второе уравнение сводится к однородному  , у которого обязательно будет нулевое решение
, у которого обязательно будет нулевое решение  . Это решение должно удовлетворять и исходному уравнению
. Это решение должно удовлетворять и исходному уравнению  , откуда
, откуда  , следовательно, любой нуль оператора
, следовательно, любой нуль оператора 
Является тривиальным, что и требовалось установить.
Из доказанного утверждения следует, что в случае отрицательного индекса 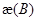 нельзя эквивалентным образом слева регулиризировать нетеров оператор
нельзя эквивалентным образом слева регулиризировать нетеров оператор  . В самом деле, индекс регуляризатора
. В самом деле, индекс регуляризатора  должен быть положительным и у него в соответствии с замечанием, сделанным в конце § 11, будет минимум
должен быть положительным и у него в соответствии с замечанием, сделанным в конце § 11, будет минимум  нулей, что, согласно лемме, исключает равносильность данного и регуляризованного уравнений.
нулей, что, согласно лемме, исключает равносильность данного и регуляризованного уравнений.
Необходимые и достаточные условия левой эквивалентной регуляризациии содержит следующая теорема С.Г. Михнина.
Теорема 2.13. Для того, чтобы оператор 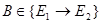 допускал левую эквивалентную регуляризацию, необходимо и достаточно, чтобы он был оператором Нетера с неотрицательным индексом.
допускал левую эквивалентную регуляризацию, необходимо и достаточно, чтобы он был оператором Нетера с неотрицательным индексом.
Доказательство. Достаточность условий теоремы вытекает из теоремы 1.13 об эквивалентной регуляризиции.
Для доказательства необходимости заметим, что по теореме 2.8. оператор  нормально разрешим. Далее,
нормально разрешим. Далее,  , так как по условию уравнения
, так как по условию уравнения 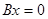 и
и  эквивалентны. Остается доказать, что
эквивалентны. Остается доказать, что  конечно и
конечно и  .
.
Уравнения  и
и  эквивалентны при любом
эквивалентны при любом  . Следовательно, условием необходимым и достаточным для разрешимости уравнения
. Следовательно, условием необходимым и достаточным для разрешимости уравнения  будут равенства, обеспечивающие разрешимость уравнения Фредгольма
будут равенства, обеспечивающие разрешимость уравнения Фредгольма  :
:
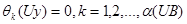 , (13.3)
, (13.3)
где  - решение уравнения
- решение уравнения  .
.
Условия (13.3) перепишем в виде
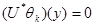 ,
,  . (13.4)
. (13.4)
Таким образом, функционалы 
 удовлетворяют уравнению
удовлетворяют уравнению  и условия (13.4) являются необходимыми и достаточными для разрешимости уравнения
и условия (13.4) являются необходимыми и достаточными для разрешимости уравнения 
. Отсюда следует, что эти функционалы исчерпывают ядро оператора  , хотя, быть может, среди них есть и линейно-зависимые, т.е.
, хотя, быть может, среди них есть и линейно-зависимые, т.е.  . Так как
. Так как  , то
, то 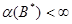 и
и  . Теорема доказана.
. Теорема доказана.
Рассмотрим теперь вопрос об эквивалентной регуляризации оператора справа.
Теорема 3.13. Для того, чтобы оператор Нетера  имел эквивалентный правый регуляризатор, необходимо и достаточно, чтобы индекс оператора
имел эквивалентный правый регуляризатор, необходимо и достаточно, чтобы индекс оператора  был неположительным.
был неположительным.
Доказательство. Достаточность условий теоремы вытекает из теоремы 1.13 об эквивалентной регуляризации.
Необходимость: пусть  - эквивалентный праый регуляризатор. Предположим, вопреки тому, что требуется доказать, что
- эквивалентный праый регуляризатор. Предположим, вопреки тому, что требуется доказать, что  . Следовательно,
. Следовательно,  , т.е.
, т.е.  , а это противоречит тому, что уравнение
, а это противоречит тому, что уравнение  разрешимо для любого
разрешимо для любого  .
.
Теорема 4.13. Пусть 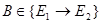 - оператор Нетера,
- оператор Нетера,  . Для того, чтобы его правый регуляризатор
. Для того, чтобы его правый регуляризатор  был эквивалентным регуляризатором, необходимо и достаточно, чтобы его
был эквивалентным регуляризатором, необходимо и достаточно, чтобы его 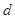 - характеристика имела вид
- характеристика имела вид  .
.
Доказательство. Необходимость: пусть  - правый эквивалентный регуляризатор. Тогда
- правый эквивалентный регуляризатор. Тогда  и уравнение
и уравнение  должно быть разрешимым при любом
должно быть разрешимым при любом  , следовательно,
, следовательно,  и
и  .
.
Достаточность: так как 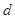 - характеристика оператора
- характеристика оператора  имеет вид
имеет вид  , то уравнение
, то уравнение  разрешимо при любом
разрешимо при любом  , т.е.
, т.е.  - эквивалентный регуляризатор.
- эквивалентный регуляризатор.
Теорема 2.13 дает полную характеристику множества операторов, допускающих левую эквивалентную регуляризацию. В случае гильбертова пространства можно дать такую же характеристику множества операторов, допускающих левую регуляризацию вообще (не обязательно эквивалентную ); И.Ц.Гохберг доказал, что для того, чтобы оператор 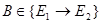 допускал левую регуляризацию, необходимо и достаточно, чтобы он был нормально разрешим и имел конечное число нулей. Однако для произвольных банаховых пространств этот факт уже не имеет места. И.Нисто доказал, что для существования левого регуляризатора у оператора
допускал левую регуляризацию, необходимо и достаточно, чтобы он был нормально разрешим и имел конечное число нулей. Однако для произвольных банаховых пространств этот факт уже не имеет места. И.Нисто доказал, что для существования левого регуляризатора у оператора 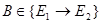 небходимо и достаточно, чтобы
небходимо и достаточно, чтобы  было конечным числом и образ
было конечным числом и образ  имел в
имел в  топологическое дополнение.
топологическое дополнение. 
Аналогичное утверждение справедливо и для правой регуляризации. Для существования у оператора 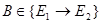 правого регуляризатора необходимо и достаточно, чтобы
правого регуляризатора необходимо и достаточно, чтобы  был конечным числом и ядро
был конечным числом и ядро  имело в
имело в  топологическое дополнение.
топологическое дополнение.
Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...