
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Принцип включення-виключення в альтернативній формі
Ця форма принципу включення-виключення використовується для розв’язування задач, де необхідно знайти кількість елементів заданої множини А, які не мають жодної з n властивостей 
Позначимо:
 – підмножина елементів, що мають властивість
– підмножина елементів, що мають властивість  ;
;
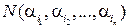 – кількість елементів множини А, які одночасно мають властивості
– кількість елементів множини А, які одночасно мають властивості  ;
;
 – кількість елементів множини А, що не мають жодної властивості
– кількість елементів множини А, що не мають жодної властивості  ;
;
N – кількість елементів множини А.
Тоді

За принципом включення-виключення отримаємо:
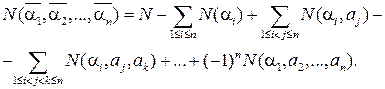
Доведення рівностей з множинами
Доводити рівності з множинами можна різними способами.
Спосіб 1. Для доведення рівності використовується теорема про те, що дві множини А та В рівні тоді й лише тоді, коли  та
та  .
.
Приклад 6.1. Доведемо рівність множин, яка є формулюванням закону де Моргана  .
.
Припустимо, що  . Тоді
. Тоді  , звідси
, звідси  або
або  . Отже
. Отже 
 або
або  , а це означає, що
, а це означає, що  . Отже, доведено, що
. Отже, доведено, що  .
.
Навпаки, нехай  . Тоді
. Тоді  або
або  , звідки
, звідки  або
або  . Це означає, що
. Це означає, що  , тобто
, тобто  . Отже
. Отже  .p
.p
Cпосіб 2.Доведення рівності множин із використанням таблиць належності. У цих таблицях розглядають усі можливі комбінації належності елементів множинам і позначають 1,якщо елемент належить множині, 0 – якщо елемент їй не належить.
Приклад 6.2. Доведемо цим способом рівність 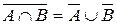 .Доведення подано у табл. 6.1.
.Доведення подано у табл. 6.1.
Таблиця 6.1
| А | В | 
| 
| 
| 
| 
|
Стовпчики, які в табл. 6.1 відповідають множинам  та
та  збіглися, отже
збіглися, отже 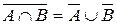 .p
.p
Спосіб 3. Доведення рівності множин з використанням законів логіки.
Приклад 6.3. Доведемо попередню рівність 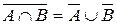 .
.
Доведення полягає в послідовній перевірці наступних рівностей


 .p
.p
Спосіб 4.Доведення рівності множин із використанням основних законів (табл. 3.1).
Приклад 6.4. Доведемо, що . Використовуючи закони де Моргана та комутативності, можна записати:
. Використовуючи закони де Моргана та комутативності, можна записати:
 – за законом де Моргана;
– за законом де Моргана;
 – за законом де Моргана;
– за законом де Моргана;
 – за законом комутативності;
– за законом комутативності;
=  – за законом комутативності. p
– за законом комутативності. p
Комп’ютерне представлення множин
Зобразити множини у комп’ютері можна різними способами. Наприклад, накопичити елементи множини в невпорядкованому вигляді. Але тоді операції із множинами вимагатимуть значних ресурсів часу, адже щоразу необхідно буде здійснювати перегляд елементів. Тому є інші способи зображення множин у комп'ютері.
Одним із найпоширеніших та найпростіших способів є зображення множин за допомогою бітових рядків. Нехай універсальна множина U містить п елементів. Упорядкуємо довільним способом елементи універсальної множини. Тоді 
Множину 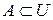 зображають у комп'ютері рядком із 0 та 1 довжини п так: якщо
зображають у комп'ютері рядком із 0 та 1 довжини п так: якщо  , то і-й біт дорівнює 1, якщо
, то і-й біт дорівнює 1, якщо  , то і-й біт дорівнює 0.
, то і-й біт дорівнює 0.
Приклад 7.1.Нехай  ,
,  ,
,  . Тоді множину A зобразимо рядком 010000110110, а множину В – рядком 110001100100. p
. Тоді множину A зобразимо рядком 010000110110, а множину В – рядком 110001100100. p
Після представлення множин у вигляді бітових рядків, легко робити операції над ними, адже це будуть порозрядні логічні операції над відповідними рядками.
Наприклад, перетин множин – це порозрядна кон'юнкція над бітовими рядками, а об'єднання множин – порозрядна диз'юнкція над бітовими рядками.
Логічні операції наведені в табл. 7.1.
Таблиця 7.1.
| аi | bi | 
| 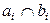
|
Приклад 7.2. Нехай 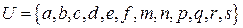 ,
,  ,
,  . Знайдемо комп'ютерне зображення перетину множин
. Знайдемо комп'ютерне зображення перетину множин  .Виконаємо порозрядну кон'юнкцію рядків, які зображають множини А та В:
.Виконаємо порозрядну кон'юнкцію рядків, які зображають множини А та В:
 = 010000110110;
= 010000110110;
 = 110001100100.
= 110001100100.
 = 010000100100.
= 010000100100.
Отже, повертаючись до звичайного зображення множин, маємо  .p
.p
Приклад 7.3. Нехай 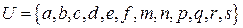 ,
,  ,
,  .Знайдемо об'єднання множин
.Знайдемо об'єднання множин  . Виконаємо порозрядну диз'юнкцію рядків, які зображають множини А та В:
. Виконаємо порозрядну диз'юнкцію рядків, які зображають множини А та В:
 = 010000110110;
= 010000110110;
 = 110001100100;
= 110001100100;
 = 110001110110.
= 110001110110.
Отже,  .p
.p
Якщо універсальна множина U має велику потужність, а підмножини універсальної множини не дуже потужні, то зображення за допомогою бітових рядків не є ефективним з точки зору витрат пам'яті. У такому разі для зображення множин доцільно використовувати інші структури даних – як правило, зв'язані списки, масиви або хеш-таблиці.
Приклади розв’язування завдань
Приклад 8.1. Задати двома різними способами множину А всіх парних чисел 2, 4, 6, ...., що не перевищують 1000.
Розв’язання:
1. Перерахуванням: А={2, 4, 6, 8, 10, …, 998, 1000};
2. Описом: А={(x|xÎN)  (х/2ÎN), N£1000}; (N – множина натуральних чисел 1, 2, 3, ….).▲
(х/2ÎN), N£1000}; (N – множина натуральних чисел 1, 2, 3, ….).▲
Приклад 8.2. Зобразіть фігури, задані множинами 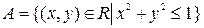 ,
,  , де
, де 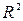 – дійсна площина. Які фігури зображають множини
– дійсна площина. Які фігури зображають множини  ?
?
Розв’язання:
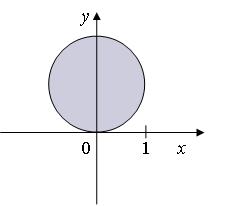

Множина А Множина В
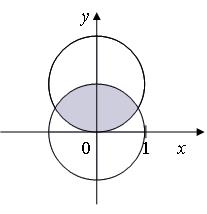

Множина  Множина
Множина 

Множина 
Приклад 8.3. Чи правильні рівності:
1) {{1,2}, {2,3}}={1,2,3}?
2) {{1,2}}={1,2}?
Розв’язання:
1) Ні, адже елементами першої множини є підмножини {1,2} та {2,3}, а другої – елементи 1,2,3.
2) Ні, тому що перша множина одноелементна, тобто складається з одного елемента – підмножини {1,2}, а друга має два елементи 1 та 2. ▲
Приклад 8.4. Перечисліть елементи наступних множин:
1) А={a|aÍB, B={1,2,3}};
2) A={a|aÎB, B={1,2,3}}.
Розв’язання:
1) Так, як аÍВ, а В – трьохелементна множина, то існує 23=8 підмножин: А={{1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}, Æ}.
2) Так, як аÎВ, то А=В={1,2,3}.▲
Приклад 8.5. Довести, використовуючи закони алгебри множин, що 
Розв’язання:
 ▲
▲
Приклад 8.6. Спростити вираз 
Розв’язання:
Використовуючи закони алгебри множин:
 ▲
▲
Приклад 8.7. Опитування 100 студентів показало, що серед них англійську мову вивчають 29 студентів, німецьку – 30, французьку – 9, лише французьку – 1, англійську та німецьку – 10, німецьку та французьку – 4, всі три мови – 3 студенти. Скільки студентів не вивчають жодної мови? Скільки студентів вивчають лише німецьку мову? У розв’язку використовувати діаграми Ейлера-Венна.
Розв’язання:
Введемо позначення:
U – множина всіх опитаних студентів;
А – множина студентів, які вивчають англійську мову;
Н – множина студентів, які вивчають німецьку мову;
Ф – множина студентів, які вивчають англійську мову.
З умови задачі очевидно, що  =3, тоді
=3, тоді  =4-3=1;
=4-3=1; 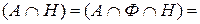 10-3=7. У такому випадку лише німецьку мову вивчають 30-7-3-1=19 студентів.
10-3=7. У такому випадку лише німецьку мову вивчають 30-7-3-1=19 студентів.
Із умови задачі також випливає, що  9-1-1-3=4, тому лише англійську мову вивчають 29-4-3-7=15 студентів. Тоді число студентів, що не вивчають жодної мови, буде рівним
9-1-1-3=4, тому лише англійську мову вивчають 29-4-3-7=15 студентів. Тоді число студентів, що не вивчають жодної мови, буде рівним  100-(1+1+3+4+7+15+19)=50 студентів.
100-(1+1+3+4+7+15+19)=50 студентів.

Рис. 8.1 Діаграма Ейлера-Венна
Приклад 8.8. Довести, що для будь-яких множин А та В виконується рівність  .
.
Розв’язання:
Для доведення використаємо метод від супротивного, тобто нехай  і
і  .
.
Із АÍВ випливає, що якщо аÎА, то аÎВ. (1)
З іншої сторони із  Ë
Ë 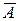 існує такий елемент а, що
існує такий елемент а, що  та
та  , отже
, отже 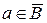 і
і  . (2)
. (2)
Використовуючи (1) та (2):
З того, що  і
і  випливає, що
випливає, що  та
та  , а звідси
, а звідси  =Æ, тобто отримали суперечність.
=Æ, тобто отримали суперечність.
Таким чином, вираз  хибний і тому
хибний і тому  , тобто
, тобто  .
.
Аналогічно можна показати, що  і, отже,
і, отже,  , що і потрібно було довести. ▲
, що і потрібно було довести. ▲
Приклад 8.9. Знайти декартовий добуток множин A={1,2,3}, B={a,b} та його потужність.
Розв’язання:
A´B = {(1,a), (1,b), (2,a), (2,b), (3,a), (3,b) },
B´A = {(a,1), (a,2), (a,3), (b,1), (b,2), (b,3) }.
Як бачимо, A´B ¹ B´A.
Потужність декартового добутку: |A´B|=|B´A| = 3×2=6. ▲
Приклад 8.10. Довести рівність множин:(AÈB)´С=(A´C)È(B´C)
Розв’язання:
Доведемо, що (AÈB)´СÍ(A´C)È(B´C).
Нехай zÎ(AÈB)´С, тоді z=(x,y), де xÎAÈB та yÎС. Отже, xÎA або xÎВ. Тобто xÎA та yÎС або xÎВ та yÎС. Тому zÎA´C або zÎB´C. За означенням об’єднання zÎ(A´C)È(B´C).
Доведемо, що (AÈB)´СÊ(A´C)È(B´C).
Нехай zÎ(A´C)È(B´C), тоді zÎA´C або zÎB´C. Так як z=(x,y), то xÎA, yÎС або xÎB, yÎС.Отже, xÎA або xÎВ при yÎС. Тому xÎAÈB і yÎС. За означенням декартового добутку zÎ(AÈB)´С. ▲
Приклад 8.11. Зобразіть на координатній площині декартовий добуток множин А×В, якщо:
a) А= {1,2,3}, В=[3,5];
b) А={х ׀ x  R, 1≤x≤3}; B={y ׀ y
R, 1≤x≤3}; B={y ׀ y  R, 3≤y≤5};
R, 3≤y≤5};
c) А=R, В=[3,5];
d) А=R, В=R.
Розв’язання:
а) Так як множина А складається з трьох елементів, а множина В містить всі дійсні числа від 3 до 5, включаючи і самі ці числа, то декартовий добуток А×В складатиметься з нескінченної кількості пар, перша компонента яких або 1, або 2, або 3, а друга – будь-яке дійсне число з проміжку [3, 5]. Безліч таких пар дійсних чисел на координатній площині зобразиться трьома відрізками (рис. 8.2).
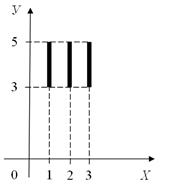
Рис. 8.2.
b) У цьому випадку нескінченними є обидві множини А і В. Тому першою координатою пари, що належить множині А×В, може бути будь-яке число з проміжку [1, 3], а другою – будь-яке число з проміжку [3,5] і, отже, точки, що зображують елементи декартового добутку даних множин А і В, утворюють квадрат (рис. 8.3).
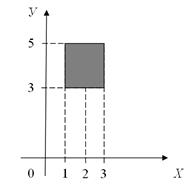
Рис. 8.3.
с) Цей випадок відрізняється від попереднього тим, що множина А складається з усіх дійсних чисел, тобто абсциса точок, що зображають елементи множини А×В, приймає всі дійсні значення, в той час як ордината вибирається з проміжку [3, 5].
Безліч таких точок утворює нескінченну смугу (рис. 8.4).
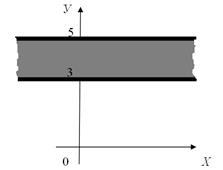
Рис. 8.4.
d) Декартовий добуток R×R складається з різноманітних дійсних чисел. Точки, що зображують ці пари, суцільно заповнюють координатну площину.
Таким чином, декартовий добуток R×R містить стільки ж елементів, скільки точок знаходиться на координатній площині. ▲
Приклад 8.12. На координатній площині побудувати множину (-1; 3]×[1; 3).
Розв’язання:
Першу множину поміщаємо на осі OX, другу на осі OY. Множина всіх пар, тобто декартовий добуток, зображається точками заштрихованого прямокутника, але без лівої та нижньої сторони (рис. 8.5).

Рис. 8.5 Декартовий добуток
Приклад 8.13. Скільки цілих чисел між 0 та 1000 містять рівно одну цифру 6?
Розв’язання:
Нехай S – множина цілих чисел між 0 та 1000, що містять рівно одну цифру 6. Розглянемо три підмножини S1, S2 та S3 множини S.
S1 – множина, яка містить число, що складається з однієї цифри і ця цифра 6;
S2 – множина, яка містить двохзначне число, що містить лише одну цифру, яка рівна 6;
S3 – множина, яка містить трьохзначне число, що містить лише одну цифру, яка рівна 6.
Множина S1 містить лише один елемент – число 6.Отже, | S1|=1.
У множині S2 кожен елемент, що містить 6, є або першою, або другою цифрою. Якщо 6 – друга цифра, то існує 8 різних чисел, які будуть стояти на першій позиції, оскільки перше число не може бути 0 або 6. Якщо 6 – перша цифра, то таких чисел 9, оскільки друга цифра не може бути рівна 6. Таким чином, S2 містить 8+9=17 елементів, тобто | S2|=17.
Елемент із S3 може містити 6 як першою, так і другою чи третьою цифрою. Якщо 6 – перша цифра, то існує 9 варіантів вибору другої цифри та 9 варіантів вибору третьої цифри. Згідно комбінаторному принципу множення, S3 містить 9 ´ 9=81 чисел з першою цифрою 6. Якщо 6 –друга цифра, то існує 9 варіантів вибору третьої цифри та 8 варіантів вибору першої цифри, оскільки перша цифра не може бути нулем. Очевидно, S3 містить 9´8=72 чисел, у яких 6 – друга цифра. Аналогічно, S3 містить 72 числа, у яких 6 – третя цифра. Отже, всього S3 містить 81+72+72=225 елементів, тобто |S3|=225.
Оскільки  та множини S1, S2 і S3 – ті, що попарно не перетинаються, тоді
та множини S1, S2 і S3 – ті, що попарно не перетинаються, тоді
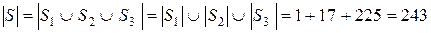 .▲
.▲
Приклад 8.14. Скільки додатних цілих чисел, менших 1001, діляться на 2, 3 чи 5?
Розв’язання:
Нехай X – множина додатних цілих чисел, які діляться на 2, 3 чи 5. Розглянемо три підмножини X1, X2 і X3 множини X.
X1 – множина додатних цілих чисел, які діляться на 2. Число елементів чи потужність цієї множини дорівнює  .
.
X2 – множина додатних цілих чисел, які діляться на 3 Число елементів чи потужність цієї множини дорівнює  .
.
X3 – множина додатних цілих чисел, які діляться на 5. Число елементів чи потужність цієї множини дорівнює  .
.
Тоді множина X1ÇX2 – множина додатних цілих чисел, які діляться на 2 або 3. Відповідно  . Множина X1ÇX3 – множина додатних цілих чисел, які діляться на 2 або 5. Тоді
. Множина X1ÇX3 – множина додатних цілих чисел, які діляться на 2 або 5. Тоді  . Множина X2ÇX3 – множина додатних цілих чисел, які діляться на 3 або 5. Аналогічно
. Множина X2ÇX3 – множина додатних цілих чисел, які діляться на 3 або 5. Аналогічно  .
.
Множина X1ÇX2ÇX3 – множина додатних цілих чисел, які діляться на 2, 3 або 5. Число елементів чи потужність цієї множини дорівнює  .
.
Використовуючи формулу включення і виключення:
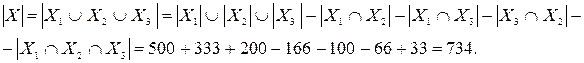
Приклад 8.15. Про множини А, B, С відомо, що:  = {1, 2, 3, 4, 5, 6},
= {1, 2, 3, 4, 5, 6},  = {3},
= {3}, 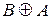 ={1, 2, 4, 6},
={1, 2, 4, 6},  ={2, 5, 6},
={2, 5, 6}, 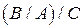 = {2},
= {2},  {1, 2, 5},
{1, 2, 5},  {1, 6}.
{1, 6}.
Знайдіть множини А, B, С.
Розв’язання:
Зобразимо перетин трьох множин A, B, C на рис. 8.6. і позначимо всеможливі утворені множини  :
:

Рис. 8.6 Приклад перетину трьох множин
Складемо систему рівнянь:
1.  =
=  {1, 2, 3, 4, 5, 6};
{1, 2, 3, 4, 5, 6};
2.  ={3};
={3};
3.  ={1, 2, 4, 6};
={1, 2, 4, 6};
4.  ={2, 5, 6};
={2, 5, 6};
5.  = {2};
= {2};
6.  ={1, 2, 5};
={1, 2, 5};
7. 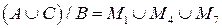 ={1, 6}.
={1, 6}.
Отримаємо:
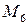 ={3},
={3},  ={2}.
={2}.
Із рівнянь (6 - 7) зрозуміло, що  ={1}.
={1}.
Тоді з рівняння (6) випливає, що  ={5}, а з рівняння (7) та (3) випливає, що
={5}, а з рівняння (7) та (3) випливає, що  , а
, а  ={6}. Із рівняння (3)
={6}. Із рівняння (3)  ={4}.
={4}.
Отже,  =
=  {1, 3, 5, 6},
{1, 3, 5, 6},
 =
=  {2, 3, 4, 5},
{2, 3, 4, 5},
 =
=  {3, 4, 6}.p
{3, 4, 6}.p
9. Завдання до виконання
1. Нехай А={{1,2,3}, {1,3}, 1, 2}. Чи справедливо, що
a) {1, 2}ÎА;
b) {1, 2}ÌA.
2. Перелічити елементи множини:
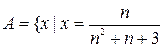 , n=1, 2,…}.
, n=1, 2,…}.
3. Перелічити елементи наступних множин:
a) 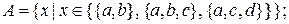
b) 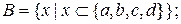
c) 
4. Нехай А – довільна множина. Що являють собою наступні множини:
a) 
b) 
c) 
d) 
5.Записати множини, перелічивши їх елементи. Яка потужність даних множин?
a) А = {n | n — додатні числа, кратні 7 і менші 60};
b) В = {x ׀ x2 - 5x + 6 = 0}.
6. Записати усі підмножини множини А ={а, b, с}.
a) Чи рівні множини {a, b, c, d}і {b, d, с, а}?
b) Нехай М = {чотирикутники}. Чи належать до множини М такі фігури: квадрат, ромб, коло, шестикутник?
7. Нехай А – множина цілих чисел, що діляться на 4, а В – множина цілих чисел, що діляться на 3. Які з чисел 9, 0, -24, -53, 128, 242048 входять у множину  ?
?
8. Нехай А = {1, 2, 3, 4, 5, 6, 7} і В = {2, 4, 6}. Знайти:
a) суму С;
b) різницю R;
c) переріз Р множин А і В.
9. Нехай Ν = {натуральні числа}, М ={додатні раціональні числа}, Р={прості числа}, Q = {додатні непарні числа}. Чи правильне твердження  ?
?
10. Нехай А – множина, що складається з 30 стільців, а В – множина, що складається з 30 студентів. Чи А=В ? Обґрунтувати відповідь.
11. За допомогою наочного зображення на площині впевнитись, що для будь-яких трьох множин А, В і С справджуються такі рівності:
a)  ;
;
b)  .
.
12. Користуючись кругами Ейлера, довести рівності:
a)  ;
;
b)  .
.
13. Вказати, які з поданих нижче множин скінченні, а які нескінченні (поясніть, чому):
a) множина цілих чисел, що діляться на 5;
b) множина коренів заданого многочлена;
c) множина всіх рослин на Землі.
14. Записати формули, відповідні до діаграм Венна:
a)  b)
b) c)
c)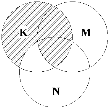 d)
d)
15. Зобразити на координатній площині декартові добутки множин А та В. У задачі b записати також усі елементи декартових добутків:
a)  ;
;
b)  .
.
16. Задані множини A={a,b,c}, B={x,y}, C={0,1}. Побудувати декартові добутки а-d:
a) 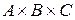 ;
;
b)  ;
;
c) 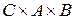 ;
;
d)  .
.
17. Задані множини А={a,b,c,d,e} та В={a,b,c,d,e,f,g,h}. Побудувати множини а-d:
a) 
b)  ;
;
c) А\В;
d) В\А.
18. Знайти множини А та В, якщо А\В={1,5,7,8}, B\A={2,10} та  ={3,6,9}.
={3,6,9}.
19. А та В – множини. Довести рівність A\B=A  .
.
20. А та В – множини . Довести рівність  .
.
21. Нехай А, В та С – довільні множини. Довести, що:
a) 
b) 
22. Задані множини А, В та С. Довести рівність множин 
23. Задані множини А={0,2,4,6,8,10}, B={0,1,2,3,4,5,6} та С={4,5,6,7,8,9,10}.
Побудувати множини:
a)  ;
;
b)  ;
;
c)  ;
;
d) 
24. Чи можна стверджувати, що А=В, якщо А, В та С – множини, для яких виконані такі рівності:
a)  ;
;
b)  ;
;
c)  .
.
25. Нехай А, В та С – довільні множини. Довести, що:

26. Множина А складається із натуральних чисел, що діляться на 4, множина В – із натуральних чисел, що діляться на 10, множина С – із натуральних чисел, що діляться на 75. Із яких чисел складається множина 
27. Дано довільні множини А, В, С такі, що:  і
і 
 і
і 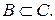
Чому рівні вирази:
a) 
b) 
28. Задано довільні множини А, В, С такі, що 
 . Чому рівні множини:
. Чому рівні множини:
a) 
b) 
c) 
d) 
29. Задані множини:
a) А={h,o,t} і B={t,o,o,t,h};
b) A={r,e,s,t} і В={s,t,r,e,e,t}.
Чи правильно, що 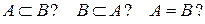
30. Відомо, що:
a) 
b)  .
.
Що випливає з даних рівнянь?
31.Задано, що S={a1, a2, a3}, причому відомо, що  , A={a1, a2};
, A={a1, a2};  , B={a2, a3};
, B={a2, a3};  ; C={a2}. Знайти елементи наступних множин:
; C={a2}. Знайти елементи наступних множин:
a) 
b) 
c) 
d) 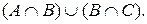
32. Нехай U={1,2,3,4,5}, X={1,5}, Y={1,2,4}, Z={2,5}.
Знайти множини:
a)  ;
;
b) 
c)  ;
;
d) 
e) 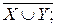
f) 
g) 
h) 
i) 
j) 
k) 
33. Нехай U ={a,b,c,d,e,f}, A={a,b,c}, B={f,e,c,a}, C={d,e,f}.
Знайти множини:
a) 
b) 
c) 
d) 
e) 
f) 
g) 
h) 
i) 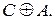
34. Задані дві довільні множини А та В такі, що  Як виглядають множини
Як виглядають множини  та
та 
35. Задані дві довільні множини С та D такі, що  Як виглядають множини
Як виглядають множини  та
та 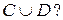
36. Задано довільну множину Х. Знайти множини:
a) 
b) 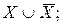
c) 
d)  .
.
37. Які з наступних тверджень правильні:
a) 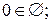
b) 
c) 
38. Спростити вирази:
a) 
b) 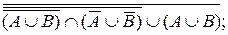
c) 
d) 
e) 
f) 
g) 
h) 
i)  .
.
39. Довести твердження, використовуючи закони алгебри множин:
a) 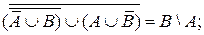
b) 
c) 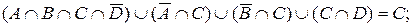
d) 
40. Для довільних множин А, В, С, D Ì U побудувати діаграми Ейлера-Венна при умові:
a) 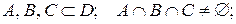
b) 
c) 
41. У студентському потоці 37 людей добре знають математику, а 25 людей – електроніку і 19 людей добре знають і математику і електроніку. Скільки студентів в потоці добре знає тільки один предмет ?
42. Із 250 студентів 151 вивчають німецьку мову, 136 – французьку мову, 27 – італійську, 63 – французьку і німецьку, 7 – італійську та французьку, 11 – німецьку та італійську, 4 – всі три мови.
a) Скільки студентів вивчають німецьку чи французьку мову?
b) Скільки студентів вивчають лише італійську мову?
c) Скільки студентів вивчають німецьку і французьку, але не італійську?
d) Скільки студентів не вивчають жодної мови?
e) Скільки студентів вивчають хоча б дві іноземні мови?
43. Знайти декартовий добуток множин А та В і зобразити його на координатній площині:
a) А={х ׀ x  N, 2 <x≤ 5}; B={y ׀ y
N, 2 <x≤ 5}; B={y ׀ y  N, 3 ≤y ≤ 8};
N, 3 ≤y ≤ 8};
b) А={х ׀ x  R, x>0}; B={y ׀ y
R, x>0}; B={y ׀ y  R, y<0};
R, y<0};
c) А={х ׀ x  R, x≤2}; B={y ׀ y
R, x≤2}; B={y ׀ y  R};
R};
d) А={х ׀ x  R, 0≤x≤1}; B={y ׀ y
R, 0≤x≤1}; B={y ׀ y  R, 3<y<5};
R, 3<y<5};
e) А={х ׀ x2 –5x+6=0}; B={y ׀y2 –1=0};
f) А={х ׀ x3– 4x=0}; B={y ׀ y2 +10y+24=0}.
44. Про множини А, B, С відомо, що:  = {1, 2, 3},
= {1, 2, 3},  = {3},
= {3},  ={3},
={3},  ={1, 2, 3, 4, 5},
={1, 2, 3, 4, 5}, 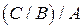 = {4, 5},
= {4, 5},  {3},
{3},  {1, 2}.
{1, 2}.
Знайдіть множини А, B, С.
45. Про множини А, B, С відомо, що:  = {a, b, c, d, e, f ,g},
= {a, b, c, d, e, f ,g},  ={a, b, c, d},
={a, b, c, d},  {a, b, c, d, e, f ,g},
{a, b, c, d, e, f ,g},  .
.
Знайдіть множини А, B, С.
46. Про множини А, B, С відомо, що:  {b, c, d},
{b, c, d},  ={a},
={a},  {a },
{a },  ={a, e, f}.
={a, e, f}.
Знайдіть множини А, B, С.
47. У спортивному таборі 55 % дітей вміють грати в футбол, 58 % — у волейбол і 93 % — у баскетбол. Яка гарантована найменша кількість дітей у % , які вміють грати і у футбол, і у баскетбол, і у волейбол?
48. У класі з 99 учнів 67 уміють плавати, 79 — грати у шахи і тільки 10 не вміють ні того, ні іншого. Скільки учнів уміють плавати і грати у шахи?
Контрольні запитання.
<Последнее изменение этой страницы: 2016-06-09
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...