
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Теорема № 3. (о пределе промежуточной переменной )
Еслидве переменные имеют один тот же предел, а третья переменная,
заключена между ними, то она имеет тот же предел.
(докажем для последовательности).
( У Письменного доказательство проведено для функций).
Дано. (1) 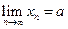 , (2)
, (2)  ,
, 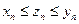
 .
.
Доказать.  .
.
Доказательство.
Из (1) 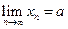 по определению предела последовательности, имеем
по определению предела последовательности, имеем
 или
или  , или
, или  .
.
Из (2)  по определению предела последовательности, имеем
по определению предела последовательности, имеем
 или
или  , или
, или  .
.
Выберем номер  , тогда
, тогда 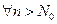 будут выполняться все три
будут выполняться все три
подчёркнутые неравенства, т.е.  . Тогда получили, что
. Тогда получили, что
 , т.е.
, т.е. 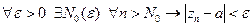 , значит доказали, что
, значит доказали, что
 .
.
Первый замечательный предел.
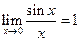
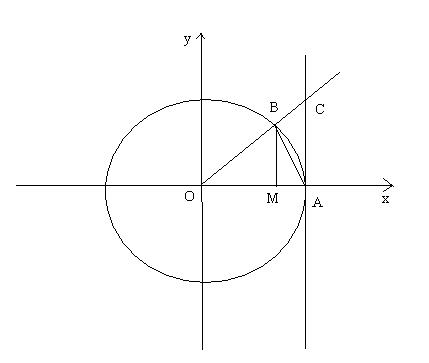
Доказательство первого замечательного предела.
1). Докажем при  . Пусть
. Пусть  , угол задан в радианной мере. На чертеже
, угол задан в радианной мере. На чертеже
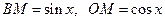 , дуга
, дуга 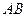 численно равна центральному углу
численно равна центральному углу 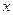 ,
,  .
.
Из чертежа видно, что 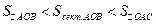 . Запишем площади полученных фигур и будем иметь следующее неравенство
. Запишем площади полученных фигур и будем иметь следующее неравенство 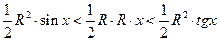 . Поделим полученное неравенство
. Поделим полученное неравенство 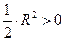 , будем иметь
, будем иметь 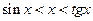 (
( 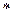 ). Так как
). Так как  ,то
,то
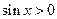 . Разделим неравенство
. Разделим неравенство 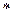 на
на 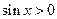 и получим следующее
и получим следующее 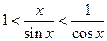 или
или
 . К последнему неравенству применим теорему о пределе промежуточной
. К последнему неравенству применим теорему о пределе промежуточной
переменной.  . Получили, что
. Получили, что 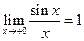 .
.
2). Докажем при 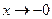 . Пусть
. Пусть 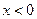 , тогда
, тогда 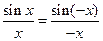 , где
, где 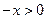 . Поэтому
. Поэтому 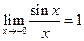 .
.
Следствия из первого замечательного предела.
1.  . Докажем.
. Докажем. 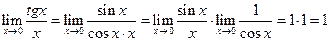 .
.
2.  . Докажем. Сделаем замену
. Докажем. Сделаем замену 


 .
.
3.  . Докажем. Сделаем замену
. Докажем. Сделаем замену 


 .
.
Второй замечательный предел
 .
.
Доказательство второго замечательного предела.
Рассмотрим переменную величину – числовую последовательность 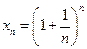 , где
, где 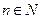 . Можно доказать, что эта последовательность возрастающая и ограниченная сверху
. Можно доказать, что эта последовательность возрастающая и ограниченная сверху 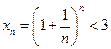 , значит по теореме Вейерштрасса о пределе монотонной последовательности делаем вывод, что
, значит по теореме Вейерштрасса о пределе монотонной последовательности делаем вывод, что  ,
, 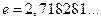
так как 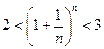 . Равенство
. Равенство 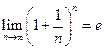 справедливо при
справедливо при 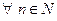 .
.
Докажем, что к числу 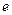 стремится и функция
стремится и функция 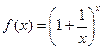 при
при  ,
,  ,
,
где  – множество действительных чисел.
– множество действительных чисел.
1 часть.Пусть 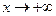 . Докажем
. Докажем 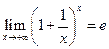 .
.
Любое действительное число 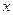 заключено между двумя натуральными числами:
заключено между двумя натуральными числами: 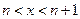 (1). Отсюда следует
(1). Отсюда следует 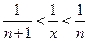 , так как
, так как 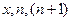 – числа положительные. Добавим к каждой части предыдущего неравенства число
– числа положительные. Добавим к каждой части предыдущего неравенства число  и получим
и получим  (2). Возведём соответственно каждую часть последнего неравенства (2)в соответствующие степени неравенства (1)и получим
(2). Возведём соответственно каждую часть последнего неравенства (2)в соответствующие степени неравенства (1)и получим
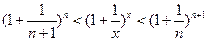 (3) .
(3) .
Найдём пределы крайних частей неравенства (3)при 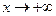 и
и 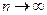 .
.
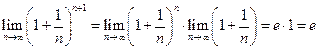 ,
,
 .
.
Применяя теорему о пределе промежуточной переменной к неравенству (3) , получим
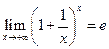 (4).
(4).
2 часть.Пусть 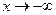 . Докажем
. Докажем  .
.
Введём новую переменную  или
или  , где
, где 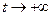 при
при 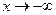 .
.
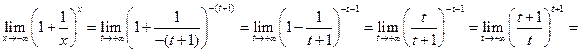

Получили  (5). Из (4)и (5)будем иметь
(5). Из (4)и (5)будем иметь  ,что и требовалось
,что и требовалось
доказать.
Замечание.Если в формуле второго замечательного предела  положить, что
положить, что 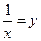 , где
, где 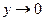 при
при  , то получим
, то получим 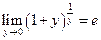 . Можно записать
. Можно записать
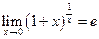 .
.
Получили две формы записи второго замечательного предела:
 и
и 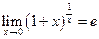 .
.
Применяется второй замечательный предел для раскрытия неопределённости 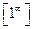 .
.
Функция  называется экспоненциальной. Обратной функцией для данной будет являться функция
называется экспоненциальной. Обратной функцией для данной будет являться функция 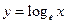 и обозначается
и обозначается 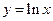 и называется натуральным логарифмом.
и называется натуральным логарифмом.
Справедливы следующие формулы  ,
, 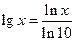 ,
,  ,
, 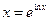 .
.
Следствия из второго замечательного предела.
1.  /в силу непрерывности функции
/в силу непрерывности функции 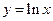 , можно поменять местами знак функции и знак
, можно поменять местами знак функции и знак  /
/  .
.
Получили формулу первого следствия:  .
.
2.  .
.
3. 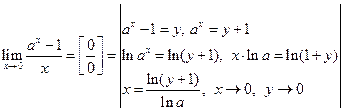 =
=  .
.
Получили формулу третьего следствия:  .
.
4. 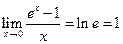 .
.
5.  .
.
Эквивалентные бесконечно малые величины.
Определение. Две бесконечно малые 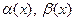 называются эквивалентными, если предел их отношения равен 1, т.е.
называются эквивалентными, если предел их отношения равен 1, т.е.  , и обозначается это так:
, и обозначается это так: 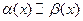 .
.
Определение.Две бесконечно малые 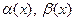 называются бесконечно малыми одного порядка малости, если предел их отношения равен постоянному числу
называются бесконечно малыми одного порядка малости, если предел их отношения равен постоянному числу  .
.
Пример:  , значит бесконечно малые
, значит бесконечно малые  и
и 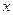 являются бесконечно малыми одного порядка малости.
являются бесконечно малыми одного порядка малости.
Определение.Если  при
при  , то бесконечно малая
, то бесконечно малая  называется бесконечно малой более высокого порядка, чем
называется бесконечно малой более высокого порядка, чем  .
.
Пример:  , значит
, значит 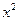 – бесконечно малая более высокого порядка, чем
– бесконечно малая более высокого порядка, чем  .
.
Замечание.При вычислении пределов можно одну бесконечно малую заменять другой ей эквивалентной более простой. Замену эквивалентными можно выполнять в частном и в произведении.
Таблица эквивалентных бесконечно малых величин.
1. 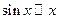
 6.
6. 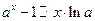

2. 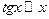
 7.
7. 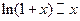

3. 
 8.
8. 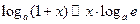

4. 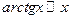
 9.
9. 

5. 

Последнее изменение этой страницы: 2016-07-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...