
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Лекция 11. Неопределенный интеграл
Интегральное исчисление
Интеграл - одно из важнейших математических понятий. Он широко применяется во многих отраслях науки, техники, экономики; имеет мировоззренческое значение.
Цель:показать,что операция дифференцирования имеет обратную операцию – интегрирование. Эта операция неоднозначная, что следует из геометрического смысла неопределенного интеграла.
Задача: научиться различать является ли данный интеграл табличным (околотабличным); овладеть способами интегрирования, позволяющими сложные интегралы сводить к табличным.
Лекция 11. Неопределенный интеграл
 11.1. Понятие первообразной и неопределенного интеграла
11.1. Понятие первообразной и неопределенного интеграла
11.2. Свойства неопределенного интеграла.
11.3. Таблица интегралов.
11.4. Некоторые методы интегрирования:
- метод подстановки;
- интегрирование некоторых выражений, содержащих в знаменателе квадратный трехчлен;
- интегрирование по частям.
11.5. Понятие о неберущихся интегралах.
Первообразная и неопределенный интеграл.
При решении многих задач физики, математики требуется по заданной функции 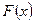 найти ее производную
найти ее производную 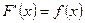 Но достаточно часто приходится сталкивать с обратными задачами, когда по известной производной
Но достаточно часто приходится сталкивать с обратными задачами, когда по известной производной 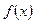 требуется найти саму функцию
требуется найти саму функцию 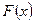 .
.
 Например, по закону измерения скорости V=V(t) необходимо найти закон движения S=S(t). Но
Например, по закону измерения скорости V=V(t) необходимо найти закон движения S=S(t). Но 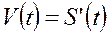 . Таким образом, по известной производной
. Таким образом, по известной производной 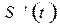 следует найти функцию
следует найти функцию  .
.
 Определение. Операция отыскания функции по ее производной называется интегрированием, а раздел математики, изучающий способы интегрирования функций – интегральным исчислением.
Определение. Операция отыскания функции по ее производной называется интегрированием, а раздел математики, изучающий способы интегрирования функций – интегральным исчислением.
Определение. Функция 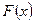 , определенная на промежутке
, определенная на промежутке 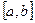 называется первообразной для функции
называется первообразной для функции 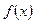 на том же отрезке, если для любого
на том же отрезке, если для любого 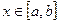 имеет место равенство
имеет место равенство 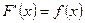
Примеры.

Очевидно, что если 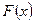 - первообразная для функции
- первообразная для функции 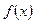 , то
, то  , где
, где 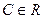 есть также первообразная той же функции.
есть также первообразная той же функции.
Действительно, пусть 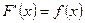 , но и
, но и  .
.
Вывод: если функция 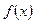 имеет хотя бы одну первообразную, то для нее существует бесчисленное множество первообразных.
имеет хотя бы одну первообразную, то для нее существует бесчисленное множество первообразных.
Теорема 11.1.
Если 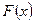 некоторая первообразная функции
некоторая первообразная функции 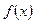 , то выражение
, то выражение  ,
,
где С – произвольная постоянная величина, исчерпывает множество всех
первообразных функции 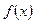 на данном промежутке.
на данном промежутке.
Доказательство.
Пусть 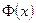 наряду с
наряду с 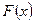 есть первообразная функции
есть первообразная функции 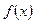 . Это означает, что:
. Это означает, что:
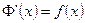

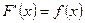
отсюда  , то есть
, то есть  ,
,
или 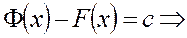
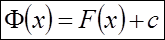 .
.
иными словами, любые первообразные функции 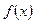 отмечаются на постоянную величину.
отмечаются на постоянную величину.
 Функция
Функция 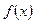 имеющая на некотором промежутке первообразную, называется интегрируемой на этом промежутке.
имеющая на некотором промежутке первообразную, называется интегрируемой на этом промежутке.
Определение. Множество всех первообразных для функции 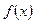 на данном промежутке называется неопределенным интегралом и обозначается следующим образом
на данном промежутке называется неопределенным интегралом и обозначается следующим образом
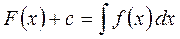
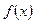 – подынтегральная функция
– подынтегральная функция
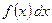 – подынтегральное выражение
– подынтегральное выражение
 Очевидно, операция интегрирования ставит соответствие функции
Очевидно, операция интегрирования ставит соответствие функции 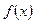 бесчисленное множество функций (первообразных)
бесчисленное множество функций (первообразных) 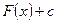 или говорят семейство функций.
или говорят семейство функций.
|
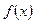 означает нахождение уравнения кривой по известному в каждой ее точке угловому коэффициенту касательной. Очевидно, в силу произвольности С таких кривых существует бесчисленное множество. Геометрически это объясняется тем, что в каждой задается лишь направление касательной, а не сама касательная. Каждая кривая
означает нахождение уравнения кривой по известному в каждой ее точке угловому коэффициенту касательной. Очевидно, в силу произвольности С таких кривых существует бесчисленное множество. Геометрически это объясняется тем, что в каждой задается лишь направление касательной, а не сама касательная. Каждая кривая 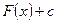 получается с параллельным любой из них вверх (вниз). Каждая из кривых называется интегральной кривой.
получается с параллельным любой из них вверх (вниз). Каждая из кривых называется интегральной кривой.
Таким образом, с геометрической точки зрения неопределенный интеграл представляет собой бесчисленное множество (или семейство) интегральных кривых.
Пример 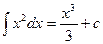 – семейство кубических парабол.
– семейство кубических парабол.
Теорема существования неопределенного интеграла.Если
подынтегральная функция 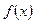 непрерывна на некотором отрезке, то она на
непрерывна на некотором отрезке, то она на
нем интегрируема.
Примеры.
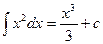 ,
, 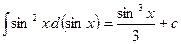 ,
, 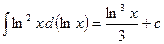
Таблица основных интегралов.
1.  7.
7. 
2.  8.
8. 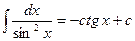
3. 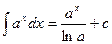 9.
9. 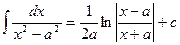
4. 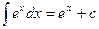 10.
10. 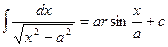
5.  11.
11. 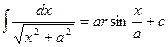
6. 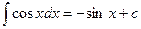 12.
12. 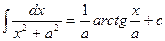
Замечание. Не путать интегралы 9 с 11 и 10 с 12.
Задача успешного интегрирования состоит в умении свети интеграл к табличному.
Примеры.
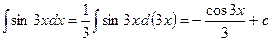
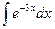
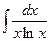

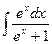
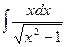

Метод подстановки.
Метод подстановки (или метод замены переменной) – один из основных методов интегрирования. Рассмотрим 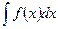 , где
, где  – непрерывная и дифференцируемая функция. Тогда
– непрерывная и дифференцируемая функция. Тогда
 (11.1)
(11.1)
Докажем.
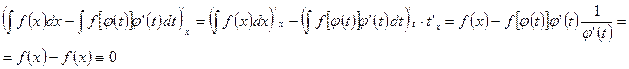 Отсюда
Отсюда
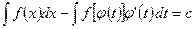
Так как неопределенные интегралы определены с точностью до постоянной, то отбросив указанную постоянную, получим формулу (11.1).
Смысл использования замены 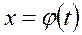 - от заданного интеграла перейти к более простому или даже табличному.
- от заданного интеграла перейти к более простому или даже табличному.
Пример 1. 
Замечание. Часто удобно вводить замену 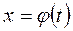 в неявном виде, то есть рассматривать новую переменную t как функцию от х
в неявном виде, то есть рассматривать новую переменную t как функцию от х 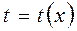 .
.
Пример 2.
 .
.
Пример 3
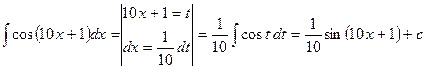 .
.
Пример.

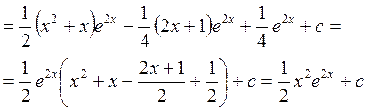
Следует иметь в виду, что по частям находят интегралы типов:
а) 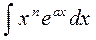 ;
;  ;
; 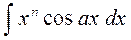 ;
;
б) 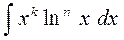 ;
; 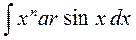 ;
;  ;
;
в)  ;
; 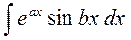 ,
,
где a, b, k – действительные числа, n – целое положительное число.
При вычислении интегралов группы «а)» принимают xn=u; при вычислении интегралов группы «б)» принимают dv=xkdx.
Формула Ньютона-Лейбница.
Рассмотрим неопределенный интеграл 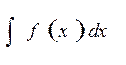 Пусть известна одна из его первообразных
Пусть известна одна из его первообразных 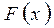 полагаем C=0, то есть
полагаем C=0, то есть 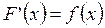 на отрезке
на отрезке  . Из дифференцируемости
. Из дифференцируемости 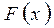 следует, что она непрерывна на отрезке
следует, что она непрерывна на отрезке  . Значит, удовлетворяет на этом отрезке теореме Лагранжа.
. Значит, удовлетворяет на этом отрезке теореме Лагранжа.




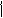






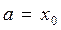
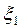
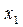
 …
… 
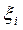
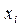 …
… 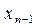
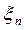

Рассмотрим разность  Разобьем отрезок
Разобьем отрезок  . Произвольно на n элементарных отрезков точками
. Произвольно на n элементарных отрезков точками 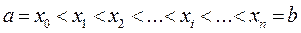
 .
.
Для каждой разности, стоящей в квадратных скобках, используем теорему Лагранжа 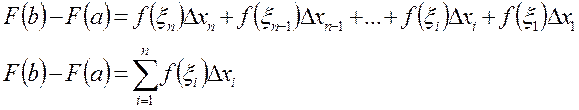
Переходя в последнем равенстве к пределу при 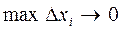 , получаем
, получаем
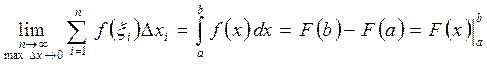
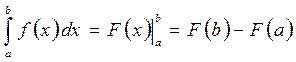 (12.7)
(12.7)
(12.7) называется формулой Ньютона-Лейбница для вычисления определенного интеграла. Эта формула устанавливает связь между определенным и неопределенным интегралами.
Возвращаясь к примеру 3, получаем 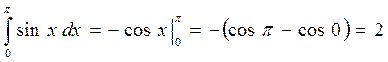
Пример 4. 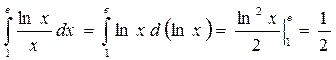
Доказательство.
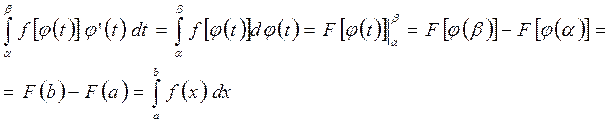
Таким образом, сравниваем левую и последнюю части, приходим к формуле (12.11).
Как и в случае с неопределенным интегралом, использование замены переменной позволяет упросить исходный интеграл, приблизив его к табличному. При этом, в отличие от неопределенного интеграла, нет необходимости возвращаться к исходной переменной интегрирования. Достаточно найти пределы изменения 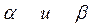 новой переменной интегрирования t, когда
новой переменной интегрирования t, когда 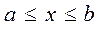 .
.
Замечание. Как и в случае неопределенного интеграла, на практике новую переменную вводят как функцию  . В этом случае пределы интегрирования новой переменной находятся совсем просто:
. В этом случае пределы интегрирования новой переменной находятся совсем просто: 
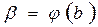
Пример. Вычислить 
Решение. Пусть  . Тогда
. Тогда 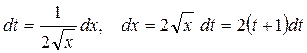 . Если
. Если  , то
, то  , если
, если  , то
, то  Следовательно,
Следовательно, 
Теорема 2. Пусть функции  и
и 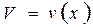 непрерывны и имеют производные на отрезке
непрерывны и имеют производные на отрезке  . Тогда
. Тогда
 (12.12)
(12.12)
Доказательство.
Как известно,  . Проинтегрируем то равенство на отрезке
. Проинтегрируем то равенство на отрезке  .
.

Но  , откуда и следует формула (12.12), которая называется формулой интегрирования по частям определенного интеграла.
, откуда и следует формула (12.12), которая называется формулой интегрирования по частям определенного интеграла.
Пример. Вычислить 
Решение.
Пусть 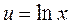 ,
,  . Тогда
. Тогда 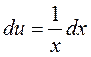 ,
, 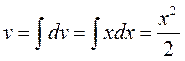
Применяя формулу (12), получаем
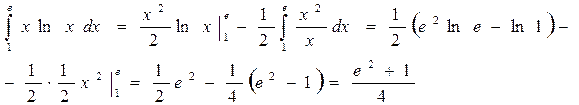
Интегральное исчисление
Интеграл - одно из важнейших математических понятий. Он широко применяется во многих отраслях науки, техники, экономики; имеет мировоззренческое значение.
Цель:показать,что операция дифференцирования имеет обратную операцию – интегрирование. Эта операция неоднозначная, что следует из геометрического смысла неопределенного интеграла.
Задача: научиться различать является ли данный интеграл табличным (околотабличным); овладеть способами интегрирования, позволяющими сложные интегралы сводить к табличным.
Лекция 11. Неопределенный интеграл
 11.1. Понятие первообразной и неопределенного интеграла
11.1. Понятие первообразной и неопределенного интеграла
11.2. Свойства неопределенного интеграла.
11.3. Таблица интегралов.
11.4. Некоторые методы интегрирования:
- метод подстановки;
- интегрирование некоторых выражений, содержащих в знаменателе квадратный трехчлен;
- интегрирование по частям.
11.5. Понятие о неберущихся интегралах.
Последнее изменение этой страницы: 2016-07-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...