
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Теорема о существовании определенного интеграла.
Если подынтегральная функция y=f(x) непрерывна на отрезке  , то она на нем интегрируема. (без доказательства)
, то она на нем интегрируема. (без доказательства)
Пример 1. 

Пример 2. 

Пример 3. 

В первых двух примерах интегралы достаточно просто вычисляются, исходя из их геометрического смысла. В третьем случае это не представляется возможным.
Таким образом, возникает задача вычисления определенного интеграла.
Вычисление определенного интеграла.
Формула Ньютона-Лейбница.
Рассмотрим неопределенный интеграл 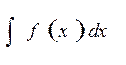 Пусть известна одна из его первообразных
Пусть известна одна из его первообразных 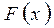 полагаем C=0, то есть
полагаем C=0, то есть 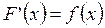 на отрезке
на отрезке  . Из дифференцируемости
. Из дифференцируемости 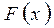 следует, что она непрерывна на отрезке
следует, что она непрерывна на отрезке  . Значит, удовлетворяет на этом отрезке теореме Лагранжа.
. Значит, удовлетворяет на этом отрезке теореме Лагранжа.




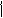






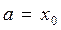
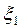
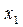
 …
… 
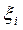
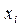 …
… 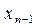
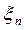

Рассмотрим разность  Разобьем отрезок
Разобьем отрезок  . Произвольно на n элементарных отрезков точками
. Произвольно на n элементарных отрезков точками 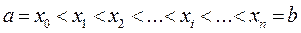
 .
.
Для каждой разности, стоящей в квадратных скобках, используем теорему Лагранжа 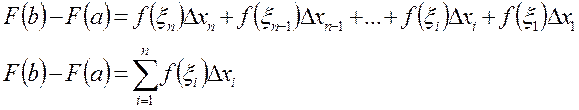
Переходя в последнем равенстве к пределу при 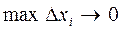 , получаем
, получаем
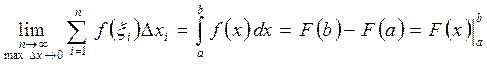
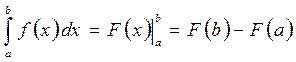 (12.7)
(12.7)
(12.7) называется формулой Ньютона-Лейбница для вычисления определенного интеграла. Эта формула устанавливает связь между определенным и неопределенным интегралами.
Возвращаясь к примеру 3, получаем 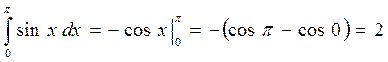
Пример 4. 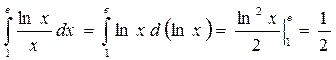
Дифференцирование определенного интеграла по переменному верхнему пределу (теорема Барроу).
Рассмотрим определенный интеграл  c переменным верхним пределом , где
c переменным верхним пределом , где  Очевидно,
Очевидно,

Заменяя x=t, получаем  определяет площадь под кривой
определяет площадь под кривой  y=f(t) при
y=f(t) при 
 (12.8)
(12.8)
Рис. 12.2
Результат (12.8) формулируется как теорема Барроу: производная от определенного интеграла по переменному верхнему пределу равна подынтегральной функции.
Свойства определенного интеграла.
1. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций

 что и требовалось доказать.
что и требовалось доказать.
2. 
3. 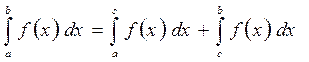 , где
, где 


Рис.12.3
4. 
5. 
6.Пусть  для
для  возрастает на отрезке
возрастает на отрезке  . Значит
. Значит  , если
, если 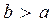
7. Пусть  на отрезке
на отрезке  ,тогда
,тогда 
Действительно, если  , то
, то  . Следовательно,
. Следовательно,  .
.
 Откуда
Откуда  .
.
Или 
Легко иллюстрируется на основании геометрического смысла.
8.Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и m и M – ее наименьшее и наибольшее значения соответственно на этом отрезке. Тогда
и m и M – ее наименьшее и наибольшее значения соответственно на этом отрезке. Тогда
 (12.9)
(12.9)
 Доказательство. По условию
Доказательство. По условию  . В соответствии со свойством (12.7)
. В соответствии со свойством (12.7)

Откуда вытекает неравенство (9)
Если  на отрезке
на отрезке  , то свойство легко иллюстрируется геометрически: площадь под кривой y=f(x) заключена между площадями прямоугольников с тем же основанием (b-a) и высотами
, то свойство легко иллюстрируется геометрически: площадь под кривой y=f(x) заключена между площадями прямоугольников с тем же основанием (b-a) и высотами 
9. Теорема о среднем. Пусть y=f(x) непрерывна на отрезке  и
и  - одна из ее первообразных (с=0). Значит
- одна из ее первообразных (с=0). Значит  . В соответствии с теоремой Лагранжа на отрезке
. В соответствии с теоремой Лагранжа на отрезке  существует точка
существует точка  в которой
в которой  . Используя формулу Ньютона-Лейбница, имеем
. Используя формулу Ньютона-Лейбница, имеем

Или окончательно
 (12.10)
(12.10)
 Полученный результат (10) формулируется как теорема о среднем: если функция y=f(x) непрерывна на отрезке
Полученный результат (10) формулируется как теорема о среднем: если функция y=f(x) непрерывна на отрезке  , то на этом отрезке найдется такая точка
, то на этом отрезке найдется такая точка  , что справедливо равенство (10)
, что справедливо равенство (10)
Если  на отрезке
на отрезке  ,то теорема о среднем легко иллюстрируется геометрически: на отрезке всегда существует такая точка
,то теорема о среднем легко иллюстрируется геометрически: на отрезке всегда существует такая точка  что площадь под кривой y=f(x) на
что площадь под кривой y=f(x) на  равна площади прямоугольника со сторонами (b-a) и f(
равна площади прямоугольника со сторонами (b-a) и f(  )
)
Найденное из равенства (12.10)
 называется средним значением функции f(x) на отрезке
называется средним значением функции f(x) на отрезке  .
.
Пример. Производительность труда рабочего в течение дня задается функцией z(t)=-0,00625t2 (денежная единица/час), где t - время в часах от начала работы  . Найти: объем произведенной продукции за один рабочий день и среднюю производительность за день.
. Найти: объем произведенной продукции за один рабочий день и среднюю производительность за день.

Среднее значение производительности за один рабочий день

Замена переменной и интегрирование по частям в определенном интеграле.
Теорема 1. Пусть на отрезке  задана непрерывная функция y=f(x) , и меющая первообразную F(x) , и пусть существует функция
задана непрерывная функция y=f(x) , и меющая первообразную F(x) , и пусть существует функция  , такая, что
, такая, что
1. 
 ; 2.
; 2. 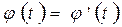 …. и…. непрерывны на отрезке
…. и…. непрерывны на отрезке  ; 3.
; 3.  непрерывна на отрезке
непрерывна на отрезке  . Тогда справедливо равенство
. Тогда справедливо равенство
 (12.11)
(12.11)
Доказательство.
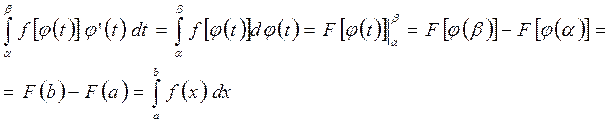
Таким образом, сравниваем левую и последнюю части, приходим к формуле (12.11).
Как и в случае с неопределенным интегралом, использование замены переменной позволяет упросить исходный интеграл, приблизив его к табличному. При этом, в отличие от неопределенного интеграла, нет необходимости возвращаться к исходной переменной интегрирования. Достаточно найти пределы изменения 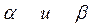 новой переменной интегрирования t, когда
новой переменной интегрирования t, когда 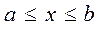 .
.
Замечание. Как и в случае неопределенного интеграла, на практике новую переменную вводят как функцию  . В этом случае пределы интегрирования новой переменной находятся совсем просто:
. В этом случае пределы интегрирования новой переменной находятся совсем просто: 
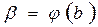
Пример. Вычислить 
Решение. Пусть  . Тогда
. Тогда 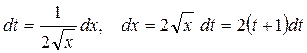 . Если
. Если  , то
, то  , если
, если  , то
, то  Следовательно,
Следовательно, 
Теорема 2. Пусть функции  и
и 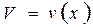 непрерывны и имеют производные на отрезке
непрерывны и имеют производные на отрезке  . Тогда
. Тогда
 (12.12)
(12.12)
Доказательство.
Как известно,  . Проинтегрируем то равенство на отрезке
. Проинтегрируем то равенство на отрезке  .
.

Но  , откуда и следует формула (12.12), которая называется формулой интегрирования по частям определенного интеграла.
, откуда и следует формула (12.12), которая называется формулой интегрирования по частям определенного интеграла.
Пример. Вычислить 
Решение.
Пусть 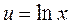 ,
,  . Тогда
. Тогда 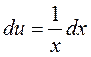 ,
, 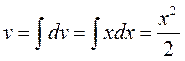
Применяя формулу (12), получаем
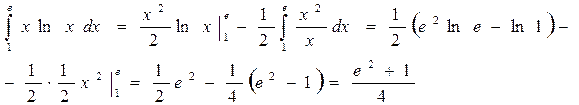
Последнее изменение этой страницы: 2016-07-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...