
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Арифметический корень натуральной степени
Приближенное значение - число
Арифметический корень натуральной степени
4Степень с действительным показателем
5Иррациональные уравнения
6Логарифмы
7Показательная функция, ее свойства и график
8Основные свойства логарифмической функции:
9Формулы и свойства логарифмов
Решение показательных уравнений и неравенств
Радианная мера угла
12Определение синуса, косинуса, тангенса и котангенса
Тригонометрические формулы
14 Тригонометрия. Свойства, графики тригонометрических функций.
|
15Графики обратных тригонометрических функций
| |||||||||
16Тригонометрические уравнения.
17Тригонометрические формулы.
18Числовая функция и способы её задания
19 Основные свойства числовых функций (, ограниченность,)
20Основные элементарные функции, их свойства и графики.
21Преобразование графиков функций
22Определение производной функции.
23Правила дифференцирования, доказательство и примеры.
24Таблица производных, производные основных элементарных функций
25Исследование функций с помощью производной
26 Алгоритмы решения стандартных задач на применение производной;
27Определение первообразной и её свойства
Таблица первообразных.
29Определенный интеграл. Как вычислить площадь фигуры
30 Правило умножения
31 Комбинаторика. Размещения, перестановки, сочетания
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Размещения, перестановки, сочетания
Размещениями множества из  различных элементов по
различных элементов по 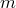 элементов называются комбинации, которые составлены из данных
элементов называются комбинации, которые составлены из данных  элементов по
элементов по 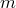 элементов и отличаются либо самими элементами, либо порядком элементов.
элементов и отличаются либо самими элементами, либо порядком элементов.
Определение. Перестановкой множества из  элементов называется расположение элементов в определенном порядке.
элементов называется расположение элементов в определенном порядке.
Число всех перестановок из  элементов обозначается
элементов обозначается 
Определение. Сочетаниями из  различных элементов по
различных элементов по  элементов называются комбинации, которые составлены из данных
элементов называются комбинации, которые составлены из данных  элементов по
элементов по  элементов и отличаются хотя бы одним элементом.
элементов и отличаются хотя бы одним элементом.
Аксиомы стереометрии и их следствия
Аксиома 1.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Аксиома 2.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую)
Аксиома 3.
Если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты
Взаимное расположение прямых в пространстве
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
– прямые совпадают.
Перпендикулярность прямых в пространстве
Определение. Две прямые называютсяперпендикулярными, если они пересекаются под прямым углом (Рис. 19).
Теорема. Прямые, которые пересекаются и соответственно параллельны перпендикулярным прямым, перпендикулярны между собой. (Рис. 20).
Перпендикулярность плоскостей
Определение. Две плоскости, которые пересекаются, называютсяперпендикулярными, если любая плоскость, перпендикулярная к прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым (Рис. 28).
Теорема. Если плоскость проходит через прямую, перпендикулярную ко второй плоскости, то эти плоскости перпендикулярны (Рис. 29).
Теорема. Если прямая, которая лежит в одной из двух перпендикулярных плоскостей, перпендикулярна к линии их пересечения, то она перпендикулярна ко второй плоскости (Рис. 30
38Углы между прямыми и плоскостями в пространстве
Определение. Две прямые, которые пересекаются, образуют смежные и вертикальные углы (Рис. 33).
Теорема. Вертикальные углы равны, а смежные дополняют друг друга к 180°.
Определение. Угловая мера более малого из углов, под которыми пересекаются две прямые, называется углом между прямыми.
Угол между перпендикулярными прямыми равняется 90° за определением. Угол между параллельными прямыми считаем таким, который равняется нулю.
Определение. Углом между скрещивающимися прямыми, называется угол между прямыми, которые пересекаются и параллельные данным скрещивающимся прямым. Этот угол не зависит от выбора прямых, которые пересекаются (Рис. 34).
Определение. Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость (Рис. 35).
Угол между параллельными прямой и плоскостью считается таким, что равняется нулю, а угол между перпендикулярными прямой и плоскостью равняется 90°. Поскольку прямая а, ее проекция а на плоскость и перпендикуляр к плоскости а в точке ее пересечения с прямой а лежат в одной плоскости, то угол между прямой и плоскостью дополняет к 90° угол между этой прямой и перпендикуляром к плоскости. Угол между параллельными плоскостями считается таким, который равняется нулю.
Определение. Углом между двумя плоскостями называется угол между прямыми, которые образуются при пересечении данных плоскостей третьей, которая проведена перпендикулярно к прямой пересечения первых двух плоскостей (Рис. 36).
Определение. Ортогональной проекцией фигуры на данную плоскость называется ее параллельная проекция, направление которой перпендикулярно к этой плоскости (Рис. 37).
Теорема. Площадь ортогональной проекции многоугольника на плоскость равняется произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.
Коллинеарные вектора
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).

|
| рис. 2 |
Вектора, параллельные одной плоскости или лежащие на одной плоскости называюткомпланарными векторами. (рис. 5).

|
| рис. 5 |
Геометрическим вектором (или вектором) называется направленный прямолинейный отрезок, для которого указано, какая из ограничивающих его точек считается началом, а какая концом.
Два вектора называются равными, если они лежат на параллельных прямых (или на одной прямой), одинаково направлены и имеют равные длины.
Вектор, у которого начало и конец совпадают, называется нулевым или нуль-вектором.
462. Определение многогранника
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.
3. Примеры многогранников
Рассмотрим следующие примеры многогранников:
1. Тетраэдр ABCD – это поверхность, составленная из четырех треугольников: АВС, ADB, BDC и ADC (рис. 1).
2. Параллелепипед ABCDA1B1C1D1 – это поверхность, составленная из шести параллелограммов (рис. 2).
4. Основные элементы многогранников
Основными элементами многогранника являются грани, ребра, вершины.
Рассмотрим тетраэдр ABCD (рис. 1). Укажем его основные элементы.
Грани: треугольники АВС, ADB, BDC, ADC.
Ребра: АВ, АС, ВС, DC, AD, BD.
Вершины: А, В, С, D.
Рассмотрим параллелепипед ABCDA1B1C1D1 (рис. 2).
Грани: параллелограммы АА1D1D, D1DСС1, ВВ1С1С, АА1В1В, ABCD, A1B1C1D1.
Ребра: АА1, ВВ1, СС1, DD1, AD, A1D1, B1C1, BC, AB, A1B1, D1C1, DC.
Вершины: A, B, C, D, A1,B1,C1,D1.
| Правильные многогранники |
  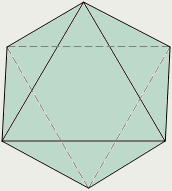 Тетраэдр Куб Октаэдр
Тетраэдр Куб Октаэдр
 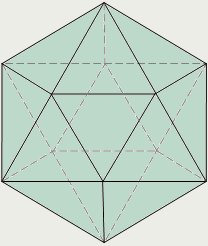 Додекаэдр Икосаэдр Додекаэдр Икосаэдр
|
| Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер. Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. |
| Призма | |
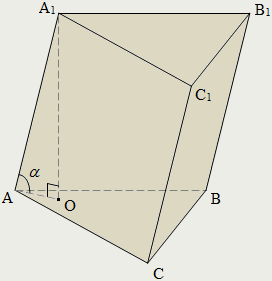
| Призмой называется многогранник, состоящий из двух плоских многоугольников, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники, о которых шла речь, называются основаниями призмы, а отрезки, соединяющие их соответствующие вершины – боковыми рёбрами призмы. Боковые рёбра призмы равны и параллельны. Поверхность призмы состоит из двух оснований и боковой поверхности. Высотой призмы называется любой из перпендикуляров, проведённых из точки одного основания к плоскости другого основания призмы. Призма называется п-угольной, если её основание – п-угольник. АВСA1В1С1 – треугольная призма; ΔАВС и ΔA1В1С1 – основания; АA1, ВВ1, СС1 – боковые рёбра; АA1В1В, АA1С1С, ВВ1С1С – боковые грани; A1О – высота призмы; α – угол наклона бокового ребра к основанию призмы. |

| Призма называется прямой, если её рёбра перпендикулярны плоскостям оснований. В противном случае призма называется наклонной. Боковые грани прямой призмы – прямоугольники. Боковое ребро прямой призмы является её высотой. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы: Sб = Pосн·АА1. Прямая призма называется правильной, если её основания являются правильными многоугольниками. |

| Сечения призмы плоскостями, параллельными боковым рёбрам,являются параллелограммами. ВВ1D1D – диагональное сечение. В любой призме площадь полной поверхности считается как сумма площади боковой поверхности и удвоенной площади основания: Sп = Sб + 2·Sосн. |
| Параллелепипед | |

| Призма, в основании которой лежит параллелограмм, называется параллелепипедом. У параллелепипеда все грани – параллелограммы. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. У параллелепипеда противолежащие грани параллельны и равны. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам. |
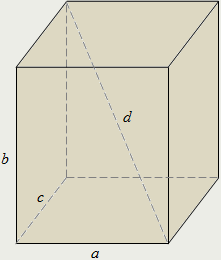
| Прямоугольным параллелепипедом называется такой прямой параллелепипед, в основании которого лежит прямоугольник. Все грани прямоугольного параллелепипеда являются прямоугольниками. В прямоугольном параллелепипеде верно: · для площади полной поверхности: Sп = 2·(ab+bc+ac); · для объёма: V = abc. |

| Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.
Диагональ куба в квадратный корень из трёх раз больше его стороны:
 В кубе верно:
· для площади полной поверхности:
Sп = 6·a², Sп = 2·d²,
· для объёма:
В кубе верно:
· для площади полной поверхности:
Sп = 6·a², Sп = 2·d²,
· для объёма:

|
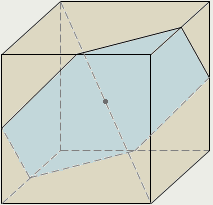
| У куба девять плоскостей симметрии: · три из них, проходя через середины четырёх параллельных ребер куба, дают в сечениях квадраты; · остальные шесть – это все плоскости диагональных сечений куба. |
| Пирамида | |
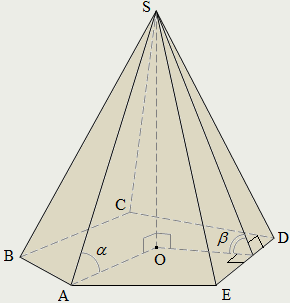
| Пирамидой называется многогранник, который состоит из плоского многоугольника (пятиугольник ABCDE) – основания пирамиды, точки (S), не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Поверхность пирамиды состоит из основания (пятиугольник ABCDE) и боковых граней. Каждая боковая грань – треугольник. Боковой поверхностью пирамиды называется сумма площадей ее боковых граней. Высотой пирамиды (SО) называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания. Пирамида называется n-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром. α – угол наклона бокового ребра SA пирамиды к плоскости её основания; β – угол наклона боковой грани (SED) пирамиды к плоскости её основания. Площадь полной поверхности любой пирамиды равна сумме площадей боковой поверхности и основания: Sп = Sб + Sосн. Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники. |
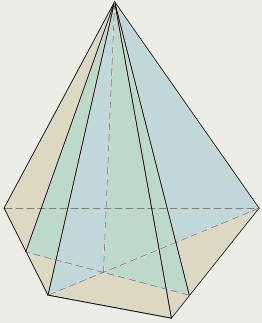
| |
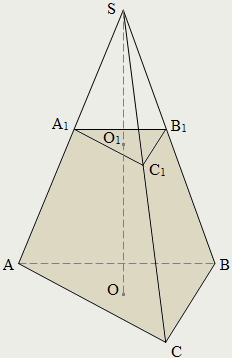
| Плоскость, которая пересекает пирамиду и параллельна её основанию, делит её на две части: пирамиду, подобную данной (SA1В1С1) и многогранник, называемый усеченной пирамидой (AВСA1В1С1). Грани усеченной пирамиды, лежащие в параллельных плоскостях (ΔАВС и ΔA1В1С1), называются основаниями, остальные грани (АA1В1В, АA1С1С, ВВ1С1С) называются боковыми гранями. Высота усеченной пирамиды (ОО1) – это расстояние между плоскостями её оснований. |

| Пирамида (например, SABCD) называется правильной, если ее основанием является правильный многоугольник (ABCD – квадрат), а основание высоты совпадает с центром этого многоугольника (О – центр описанной и вписанной окружностей основания). Осью правильной пирамиды называется прямая, содержащая ее высоту. Боковые ребра правильной пирамиды равны. Боковые грани правильной пирамиды – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды (SL), проведенная из ее вершины к стороне основания, называется апофемой. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему: Sб = ½Pосн·SL. |

| Усеченная пирамида (например, АВСDA1В1С1D1), которая получается из правильной пирамиды, также называется правильной. |
48Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости[1].
Примеры тел вращения
· Шар — образован полукругом, вращающимся вокруг диаметра разреза
· Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон
За площадь боковой поверхности цилиндра принимается площадь его развертки: Sбок = 2πrh.
· Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов
За площадь боковой поверхности конуса принимается площадь ее развертки: Sбок = πrl Площадь полной поверхности конуса: Sкон = πr(l+ r)
Объём тел вращения
Вращение вокруг оси x
Объём тела, образуемого вращением вокруг оси 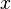 фигуры, ограниченной функцией
фигуры, ограниченной функцией  на интервале
на интервале  , осью
, осью 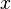 и прямыми
и прямыми  и
и  равен:
равен:

Вращение вокруг оси y[править | править вики-текст]
Объём тела, образуемого вращением вокруг оси  фигуры, ограниченной функцией
фигуры, ограниченной функцией  на интервале
на интервале  , осью
, осью  и прямыми
и прямыми  и
и  равен:
равен:

Альтернативные формулы вычисления  :
:
 и
и 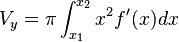
Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственнойкривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения.
· Сфера (получается вращением окружности вокруг оси, лежащей в той же плоскости и проходящей через её центр).
· Конус получается вращением прямой вокруг другой прямой, пересекающей первую.
· Круговая цилиндрическая поверхность
Площадь[править | править вики-текст]
Площадь поверхности вращения, образованной вращением плоской кривой конечной длины вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равна произведению длины кривой на длину окружности с радиусом, равным расстоянию от оси до центра масс кривой.
Объём
Объём, ограниченный поверхностью вращения, образованной вращением плоской замкнутой несамопересекающейся кривой вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равен произведению площади плоской фигуры, ограниченной кривой, на длину окружности с радиусом, равным расстоянию от оси до центра тяжести плоской фигуры.
Объём поверхности вращения, образованной вращением кривой  вокруг оси
вокруг оси  можно вычислить по формуле
можно вычислить по формуле

Цилиндр
Прямым круговым цилиндром называется тело, образованное вращением прямоугольника вокруг своей стороны.
|
Основания цилиндра – равные круги, расположенные в параллельных плоскостях.
Высотой цилиндра называют также расстояние между плоскостями его оснований. Отрезок, соединяющий точки окружностей оснований и перпендикулярный плоскостям оснований, называется образующей цилиндра .
Радиусом цилиндра называется радиус его основания.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через ось вращения. Все осевые сечения цилиндра – равные прямоугольники
Плоскость, содержащая образующую и перпендикулярная осевому сечению, проходящему через эту образующую, называется касательной к цилиндру плоскостью.
Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра.
Конус (от др.-греч. κώνος «сосновая шишка»[1]) — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник, такой конус является пирамидой.

| Геометрические фигуры. Шар, сфера. | ||||||||
|
Цилиндр
Цилиндру можно дать такое определение:
Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов. Эти круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки оснований, — образующими цилиндра.
Если образующие перпендикулярны основаниям, то цилиндр называется прямым цилиндром.
Мы будем рассматривать только прямые цилиндры. Прямой цилиндр можно получить, если свернуть в трубочку прямоугольный лист бумаги и закрыть кругами отверстия с двух концов.
O
h
O1
r
Высота цилиндра — это отрезок, соединяющий основания и перпендикулярный основаниям цилиндра.
Каждая образующая прямого цилиндра равна высоте.
Если h — высота цилиндра, а r — радиус основания цилиндра, то объем цилиндра и площадь его поверхности можно легко найти с помощью следующих формул:
- Объем цилиндра: V=πr2h,
- Площадь боковой поверхности цилиндра: Sбок=2πrh,
- Площадь полной поверхности: S=2πr(r+h).
Если не удается сразу запомнить эти формулы — не беда. Они легко выводятся из теорем планиметрии:
Основание цилиндра — это круг радиусом r. Поэтому его площадь равна πr2. Чтобы получить объем, нужно умножить площадь основания на высоту: V=Sh=πr2h.
Если развернуть боковую поверхность цилиндра на плоскость, то получится прямоугольник, одна сторона которого равна высоте (h), а другая — длине окружности основания (2πr). Площадь боковой поверхности равна произведению сторон этого прямоугольника. Чтобы найти площадь полной поверхности, нужно к площади боковой поверхности добавить две площади основания: S=2πrh+2·πr2=2πr(r+h).
Используйте эти формулы для решения следующей задачи:
Начало формы
Чему равна образующая цилиндра, радиус основания которого равен
| π |
, а площадь боковой поверхности равна 2?
Конец формы
Нефтехранилища делают в форме цилиндра из листовой стали (в верхней части лист тоньше, чем в нижней, что соответсвует распределению нагрузки на стенку). Первое такое нефтехранилище построил Владимир Шухов в 1878 году (тот самый, который потом построил Шаболовскую башню в Москве). До него нефть в России хранилась в прудах под открытым небом, а в Америке — в прямоугольных резервуарах. Как показал Шухов, форма цилиндра оптимальная с точки зрения экономии стали. Поэтому такие нефтехранилища сейчас используются по всему миру.
Чему (примерно) равен объем нефтехранилища диаметром 60 метров и высотой 18 метров? (выберите наиболее близкий вариант)
· 5000м3
· 15000м3
· 50000м3
· 100000м3
·
Следующий важнейший пример тела вращения — это шар.
Шар
Шар — тело, состоящее из всех точек пространства, находящихся на расстоянии не более R от некоторой точки, которая называется центром шара. R называется радиусом шара.
Сфера — это поверхность шара. Сфера является множеством точек, отстоящих от ее центра на расстояние R.
R
Основные свойства шара:
- Все сечения шара плоскостью — это круги;
- Сечение, проходящее через центр шара, имеет наибольший радиус и площадь.
Если R — радиус шара, то
- Объем шара равен V=
- πR3,
- Площадь поверхности шара равна S=4πR2.
Эти формулы следует запомнить. Чтобы было легче запомнить, например, формулу объема, запомните, что шар радиусом 1 имеет объем чуть больше 4.
Шар имеет наименьшую поверхность среди тел с заданным объемом. Поэтому из-за поверхностного натяжения капля воды и мыльный пузырь стремятся к форме шара.
Начало формы
Чему равен объем шара с площадью поверхности 9π? π
Конец формы
Вот еще одно интересное свойство шара:
Если провести две плоскости на расстоянии h друг от друга, которые высекают кольцо на поверхности шара, то площадь этого кольца будет равна 2πrh, где r — радиус шара.
То есть площадь кольца будет зависеть только от расстояния между плоскостями h, а не от того, в каком месте проходят плоскости. Цилиндр с высотой h и радиусом r будет иметь точно такую же площадь боковой поверхности.
Представьте себе апельсин, который порезали слоями равной толщины. Площадь оранжевой корки у каждого слоя будет одинаковой! Слой, который ближе к центру, будет длиннее, но оранжевая полоска будет уже, а у полюса — наоборот — полоска короткая, но широкая из-за наклона корки в этом месте.
Из этого свойства можно вывести формулу площади сферы. Если положить h=2r, то получим что площадь сферы равна площади боковой поверхности цилиндра, диаметр и высота которого равны диаметру сферы. То есть S=2πr(2r)=4πr2.
Конус
Конус — это тело, которое получается при объединении всех отрезков, соединяющих точки круга (основание конуса) с вершиной конуса.
Прямой конус — это конус, вершина которого лежит на прямой, перпендикулярной основанию и проходящей через центр основания. Эта прямая называетсяосью прямого конуса.
Высота конуса — это отрезок, проведенный из вершины конуса к основанию перпендикулярно основанию конуса. Отрезок, который соединяет вершину конуса с окружностью в основании, называется образующей конуса.
l
r
h
A
O
B
В задачах ЕГЭ рассматривается в основном прямой конус.
Прямой конус можно получить, если из бумажного круга вырезать сектор (с любым углом от 0 до 2π), потом свернуть его в рупор, склеить по разрезу, а круглое отверстие закрыть кругом.
Если l — длина образующей конуса, h — высота конуса, а r — радиус основания конуса, то
- Объем конуса: V=
- πr2h,
- Площадь боковой поверхности конуса: Sбок=πrl,
- Площадь полной поверхности: S=πr(r+l),
- Образующая конуса: l=√h2+r2.
Заметим, что формула объема конуса очень похожа на формулу объема пирамиды. Это следует из того, что конус — это, по сути, та же пирамида, только вместо многоугольника в основании находится круг.
Формула для образующей конуса следует из теоремы Пифагора. Она является гипотенузой прямоугольного треугольника, катеты которого — это высота конуса и радиус основания конуса. Поэтому также верны формулы: h=√l2−r2 иr=√l2−h2.
Формулу площади боковой поверхности можно получить, если рассмотреть развертку его боковой поверхности на плоскость. Она представляет собой сектор круга радиуса l. При развертке вершина конуса переходит в центр круга, образующая — в его радиус, а окружность основания — в дугу сектора. Длина дуги сектора равна длине окружности основания конуса: 2πr. Обозначим радианную меру угла сектора через α. Тогда длина его дуги равна αl, а площадь равна
1/2αl2. Тогда αl=2πr. Значит, α=
| 2πr/l |
. Тогда площадь сектора равна 1/2
| 2πr/l |
·l2=πrl.
Приближенное значение - число
Арифметический корень натуральной степени
4Степень с действительным показателем
5Иррациональные уравнения
6Логарифмы
7Показательная функция, ее свойства и график
8Основные свойства логарифмической функции:
9Формулы и свойства логарифмов
Последнее изменение этой страницы: 2016-07-22
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...


 Определения, связанные с понятием шара.
Определения, связанные с понятием шара.

