Физические величины, имеющие не только абсолютное значение, но и направление, называются векторными.

Скорость, сила, ускорение — векторы. Для них важно «сколько» и важно «куда». Например, ускорение свободного падения 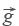направлено к поверхности Земли, а величина его равна 9,8 м/с². Импульс, напряженность электрического поля, индукция магнитного поля — тоже векторные величины.

Вы помните, что физические величины обозначают буквами, латинскими или греческими. Стрелочка над буквой показывает, что величина является векторной:

Вот другой пример.
Автомобиль движется из A в B. Конечный результат — его перемещение из точки A в точку B, то есть перемещение на вектор .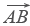

Длиной вектора называется длина этого отрезка. Обозначается: или

Понятия «больше» и «меньше» для векторов не существует — ведь направления их могут быть разными. Сравнивать можно только длины векторов.

А вот понятие равенства для векторов есть.
Равными называются векторы, имеющие одинаковые длины и одинаковое направление. Это значит, что вектор можно перенести параллельно себе в любую точку плоскости.
Единичным называется вектор, длина которого равна 1. Нулевым — вектор, длина которого равна нулю, то есть его начало совпадает с концом.

Сложение векторов

Для сложения векторов есть два способа.

1. Правило параллелограмма. Чтобы сложить векторы и , помещаем начала обоих в одну точку. Достраиваем до параллелограмма и из той же точки проводим диагональ параллелограмма. Это и будет сумма векторов и .

2. Второй способ сложения векторов — правило треугольника. Возьмем те же векторы и . К концу первого вектора пристроим начало второго. Теперь соединим начало первого и конец второго. Это и есть сумма векторов и .

Вычитание векторов

Вектор направлен противоположно вектору . Длины векторов и равны.

Теперь понятно, что такое вычитание векторов. Разность векторов и — это сумма вектора и вектора .

Умножение вектора на число

При умножении вектора на число k получается вектор, длина которого в k раз отличается от длины . Он сонаправлен с вектором , если k больше нуля, и направлен противоположно , если k меньше нуля.

Свойства операций над векторами.

свойства операций над векторами.

1. Свойство коммутативности .

2. Свойство ассоциативности сложения .

3. Существует нейтральный элемент по сложению, которым является нулевой вектор , и .

4. Для любого ненулевого вектора существует противоположный вектор и верно равенство .

5. Первое распределительное свойство .

6. Второе распределительное свойство .

Коллинеарные вектора

Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).

рис. 2

Вектора, параллельные одной плоскости или лежащие на одной плоскости называюткомпланарными векторами. (рис. 5).

рис. 5

Геометрическим вектором (или вектором) называется направленный прямолинейный отрезок, для которого указано, какая из ограничивающих его точек считается началом, а какая концом.

Два вектора называются равными, если они лежат на параллельных прямых (или на одной прямой), одинаково направлены и имеют равные длины.

Вектор, у которого начало и конец совпадают, называется нулевым или нуль-вектором.

462. Определение многогранника

Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть многогранной поверхностью или многогранником.

3. Примеры многогранников

Рассмотрим следующие примеры многогранников:

1. Тетраэдр ABCD – это поверхность, составленная из четырех треугольников: АВС, ADB, BDC и ADC (рис. 1).

2. Параллелепипед ABCDA₁B₁C₁D₁ – это поверхность, составленная из шести параллелограммов (рис. 2).

4. Основные элементы многогранников

Основными элементами многогранника являются грани, ребра, вершины.

Рассмотрим тетраэдр ABCD (рис. 1). Укажем его основные элементы.

Грани: треугольники АВС, ADB, BDC, ADC.

Ребра: АВ, АС, ВС, DC, AD, BD.

Вершины: А, В, С, D.

Рассмотрим параллелепипед ABCDA₁B₁C₁D₁ (рис. 2).

Грани: параллелограммы АА₁D₁D, D₁DСС₁, ВВ₁С₁С, АА₁В₁В, ABCD, A₁B₁C₁D₁.

Ребра: АА₁, ВВ₁, СС₁, DD₁, AD, A₁D₁, B₁C₁, BC, AB, A₁B₁, D₁C₁, DC.

Вершины: A, B, C, D, A₁,B₁,C₁,D₁.

Правильные многогранники

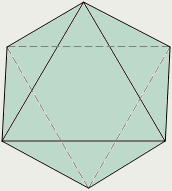Тетраэдр Куб Окт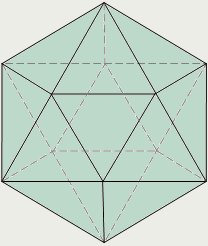аэдр   Додекаэдр Икосаэдр

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон и в каждой вершине многогранника сходится одно и то же число ребер. Существует пять типов правильных выпуклых многогранников: правильный тетраэдр, куб, октаэдр, додекаэдр, икосаэдр.

 

 

Призма
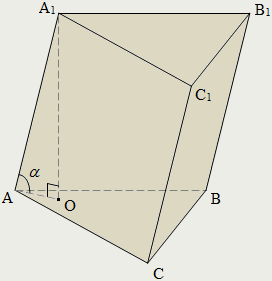
	Призмой называется многогранник, состоящий из двух плоских многоугольников, которые лежат в разных плоскостях и совмещаются параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники, о которых шла речь, называются основаниями призмы, а отрезки, соединяющие их соответствующие вершины – боковыми рёбрами призмы. Боковые рёбра призмы равны и параллельны. Поверхность призмы состоит из двух оснований и боковой поверхности. Высотой призмы называется любой из перпендикуляров, проведённых из точки одного основания к плоскости другого основания призмы. Призма называется п-угольной, если её основание – п-угольник. АВСA1В1С1 – треугольная призма; ΔАВС и ΔA1В1С1 – основания; АA1, ВВ1, СС1 – боковые рёбра; АA1В1В, АA1С1С, ВВ1С1С – боковые грани; A1О – высота призмы; α – угол наклона бокового ребра к основанию призмы.
	Призма называется прямой, если её рёбра перпендикулярны плоскостям оснований. В противном случае призма называется наклонной. Боковые грани прямой призмы – прямоугольники. Боковое ребро прямой призмы является её высотой. Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы: Sб = Pосн·АА1. Прямая призма называется правильной, если её основания являются правильными многоугольниками.
	Сечения призмы плоскостями, параллельными боковым рёбрам,являются параллелограммами. ВВ1D1D – диагональное сечение. В любой призме площадь полной поверхности считается как сумма площади боковой поверхности и удвоенной площади основания: Sп = Sб + 2·Sосн.
Параллелепипед
	Призма, в основании которой лежит параллелограмм, называется параллелепипедом. У параллелепипеда все грани – параллелограммы. Грани параллелепипеда, не имеющие общих вершин, называются противолежащими. У параллелепипеда противолежащие грани параллельны и равны. Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
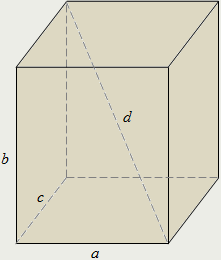
	Прямоугольным параллелепипедом называется такой прямой параллелепипед, в основании которого лежит прямоугольник. Все грани прямоугольного параллелепипеда являются прямоугольниками. В прямоугольном параллелепипеде верно: · для площади полной поверхности: Sп = 2·(ab+bc+ac); · для объёма: V = abc.
	Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом. Диагональ куба в квадратный корень из трёх раз больше его стороны: В кубе верно: · для площади полной поверхности: Sп = 6·a², Sп = 2·d², · для объёма:
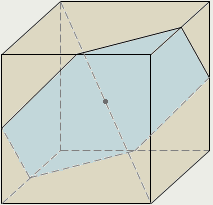
	У куба девять плоскостей симметрии: · три из них, проходя через середины четырёх параллельных ребер куба, дают в сечениях квадраты; · остальные шесть – это все плоскости диагональных сечений куба.
Пирамида
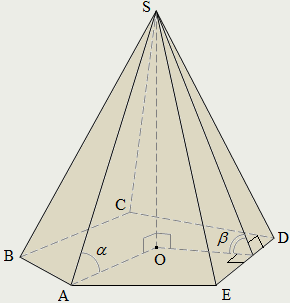
	Пирамидой называется многогранник, который состоит из плоского многоугольника (пятиугольник ABCDE) – основания пирамиды, точки (S), не лежащей в плоскости основания,– вершины пирамиды и всех отрезков, соединяющих вершину пирамиды с точками основания. Поверхность пирамиды состоит из основания (пятиугольник ABCDE) и боковых граней. Каждая боковая грань – треугольник. Боковой поверхностью пирамиды называется сумма площадей ее боковых граней. Высотой пирамиды (SО) называется перпендикуляр, проведённый из вершины пирамиды к плоскости основания. Пирамида называется n-угольной, если ее основанием является n-угольник. Треугольная пирамида называется также тетраэдром. α – угол наклона бокового ребра SA пирамиды к плоскости её основания; β – угол наклона боковой грани (SED) пирамиды к плоскости её основания. Площадь полной поверхности любой пирамиды равна сумме площадей боковой поверхности и основания: Sп = Sб + Sосн. Сечения пирамиды плоскостями, проходящими через ее вершину, представляют собой треугольники.
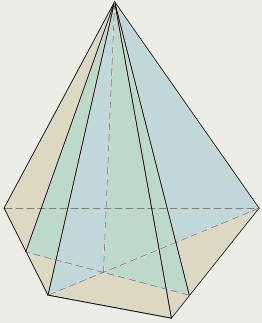
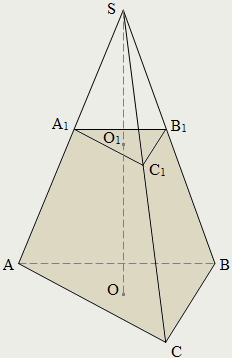
	Плоскость, которая пересекает пирамиду и параллельна её основанию, делит её на две части: пирамиду, подобную данной (SA1В1С1) и многогранник, называемый усеченной пирамидой (AВСA1В1С1). Грани усеченной пирамиды, лежащие в параллельных плоскостях (ΔАВС и ΔA1В1С1), называются основаниями, остальные грани (АA1В1В, АA1С1С, ВВ1С1С) называются боковыми гранями. Высота усеченной пирамиды (ОО1) – это расстояние между плоскостями её оснований.
	Пирамида (например, SABCD) называется правильной, если ее основанием является правильный многоугольник (ABCD – квадрат), а основание высоты совпадает с центром этого многоугольника (О – центр описанной и вписанной окружностей основания). Осью правильной пирамиды называется прямая, содержащая ее высоту. Боковые ребра правильной пирамиды равны. Боковые грани правильной пирамиды – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды (SL), проведенная из ее вершины к стороне основания, называется апофемой. Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему: Sб = ½Pосн·SL.
	Усеченная пирамида (например, АВСDA1В1С1D1), которая получается из правильной пирамиды, также называется правильной.

 

 

48Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости^[1].

Примеры тел вращения

· Шар — образован полукругом, вращающимся вокруг диаметра разреза

· Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон

За площадь боковой поверхности цилиндра принимается площадь его развертки: Sбок = 2πrh.

· Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов

За площадь боковой поверхности конуса принимается площадь ее развертки: Sбок = πrl Площадь полной поверхности конуса: Sкон = πr(l+ r)

Объём тел вращения

Вращение вокруг оси x

Объём тела, образуемого вращением вокруг оси 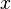фигуры, ограниченной функцией на интервале , осью 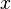и прямыми и равен:

Вращение вокруг оси y[править | править вики-текст]

Объём тела, образуемого вращением вокруг оси фигуры, ограниченной функцией на интервале , осью и прямыми и равен:

Альтернативные формулы вычисления :

и

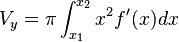
Поверхность вращения — поверхность, образуемая при вращении вокруг прямой (оси поверхности) произвольной линии (прямой, плоской или пространственнойкривой). Например, если прямая пересекает ось вращения, то при её вращении получится коническая поверхность, если параллельна оси — цилиндрическая, если скрещивается с осью — однополостный гиперболоид вращения.

· Сфера (получается вращением окружности вокруг оси, лежащей в той же плоскости и проходящей через её центр).

· Конус получается вращением прямой вокруг другой прямой, пересекающей первую.

· Круговая цилиндрическая поверхность

Площадь[править | править вики-текст]

Площадь поверхности вращения, образованной вращением плоской кривой конечной длины вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равна произведению длины кривой на длину окружности с радиусом, равным расстоянию от оси до центра масс кривой.

Объём

Объём, ограниченный поверхностью вращения, образованной вращением плоской замкнутой несамопересекающейся кривой вокруг оси, лежащей в плоскости кривой, но не пересекающей кривую, равен произведению площади плоской фигуры, ограниченной кривой, на длину окружности с радиусом, равным расстоянию от оси до центра тяжести плоской фигуры.

Объём поверхности вращения, образованной вращением кривой вокруг оси можно вычислить по формуле

Цилиндр

Прямым круговым цилиндром называется тело, образованное вращением прямоугольника вокруг своей стороны.

Основания цилиндра – равные круги, расположенные в параллельных плоскостях.

Высотой цилиндра называют также расстояние между плоскостями его оснований. Отрезок, соединяющий точки окружностей оснований и перпендикулярный плоскостям оснований, называется образующей цилиндра .

Радиусом цилиндра называется радиус его основания.

Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через ось вращения. Все осевые сечения цилиндра – равные прямоугольники

Плоскость, содержащая образующую и перпендикулярная осевому сечению, проходящему через эту образующую, называется касательной к цилиндру плоскостью.

Образующая цилиндра при вращении вокруг оси образует боковую (цилиндрическую) поверхность цилиндра.

Конус (от др.-греч. κώνος «сосновая шишка»^[1]) — тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность. Иногда конусом называют часть такого тела, имеющую ограниченный объём и полученную объединением всех отрезков, соединяющих вершину и точки плоской поверхности (последнюю в таком случае называют основанием конуса, а конус называют опирающимся на данное основание). Если основание конуса представляет собой многоугольник, такой конус является пирамидой.

Геометрические фигуры. Шар, сфера.

Шаровой (сферической) – другими словами границей шара – поверхностью является геометрическое место точек (т.е. множество всех точек) в пространстве, которые равноудалены от одной точки O, называющейся центром сферической поверхности. Каждый отрезок, который соединяет центр шара и точку на шаровой поверхности, тоже называют радиусом.   Отрезок, который соединяет 2 точки шаровой поверхности и который проходит сквозь центр шара, называется диаметр.   Эта точка О называется центром сферы, а расстояние AO, в свою очередь, называется радиусом сферы.   Сфера является поверхностью (границей) шара с центром и радиусом, как у сферы.   Шар — это тело правильно геометрической формы, ограниченное поверхностью шара. Шар возможно получить, методом вращения полукруга/круга около диаметра. Основные геометрические формулы шара (сферы). Площадь поверхности S и объём V шара радиуса r, диаметра d можно определить по формулам:     Определения, связанные с понятием шара.       Части шара.   Часть шара (сферы), которая отсекается от него любой плоскостью (ABC), является шаровым (сферическим) сегментом. Круг ABC является основанием шарового сегмента. Отрезок MN перпендикуляра, который проведен из центра N круга ABC до пересечения со сферической поверхностью, является высотой шарового сегмента. Точка M является вершиной шарового сегмента.   Часть сферы, которая заключена между 2-мя плоскостями, которые параллельны ABC и DEF, которые пересекают сферическую поверхность, является шаровым слоем. Кривая поверхность шарового слоя является шаровым поясом. Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота. Часть шара, которая ограничена кривой поверхностью сферического сегмента (AMCB) и конической поверхностью OABC, основанием у нее является основание сегмента (ABC), а вершиной – центр шара O, называется шаровым сектором.   Формулу объёма шара можно объяснить следующими рассуждениями. В шаре возможно разместить огромное количество пирамид с очень маленькими основаниями, разместив пирамиды таким образом, чтобы их вершины располагались в центре шара, а основания лежали бы на поверхности шара и эти пирамиды соприкасались бы боковыми гранями.