
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
МОСКОВСКИЙ ГУМАНИТАРНО-ЭКОНОМИЧЕСКИЙ
МОСКОВСКИЙ ГУМАНИТАРНО-ЭКОНОМИЧЕСКИЙ
ИНСТИТУТ
Учебное пособие и задачник по методам принятия решений для студентов МГЭИ
Москва 2016
Шувалова Т.И.
Учебное пособие и задачник по методам принятия решений для студентов МГЭИ. – М.: МГЭИ, 2016. – с.
Одобрено кафедрой математики и информатики. Протокол заседания кафедры от «__» _______ 2015 г. № __. Для студентов Московского гуманитарно-экономического института для всех факультетов
№
© Московский гуманитарно-
экономический институт, 201
Содержание
Предисловие………………………………………………………………………….
Основные подходы к решению многокритериальных задач…
Метод анализа иерархий ……………………………………………………..
Принятие решений в условиях неопределённости и риска..
Дерево решений…………………………………………………………………
Принятие решений на основе теории игр………………………….
Основы анализа и принятия групповых решений………………
Список литературы………………………………………………………………
Предисловие
Реальные ситуации в современном мире требуют от любого члена общества постоянно принимать решения, как в личном так и в общественном плане. Часто люди принимают решения на основе интуиции, предыдущего опыта, совета близких или уважаемых людей. Но в современном мире решение, принятое руководителем, может изменить жизнь не только его личную, но и целого коллектива, страны, а в некоторых случаях и всего мира .
Человек, принимающий решение не может всё учесть. Личность ЛПР, во многом определяет решение. Многие из последствий принятого решения ЛПР плохо себе представляет, а во многих случаях такие последствия не поддаются прогнозированию. Многие предлагают заменить ЛПР компьютером, но это практически невозможно, так как не всё можно учесть математически, компьютер может только принимать определённый класс решений и помогать в оценке решений в других случаях, когда человек не в состоянии быстро оценить очень большой объём данных. Человек обладает уникальным умением быстро оценивать ситуацию, выделять главное и отбрасывать второстепенное, соизмерять противоречивые оценки, интуитивно восполнять недостающие данные. То есть роль человека в принятии решения очень высока.
Основные подходы к решению многокритериальных задач
Существует ряд классических задач принятия решений, для которых построены отработанные математические модели, позволяющие находить решения без участия ЛПР. Это такие задачи, как распределение ресурсов, транспортная задача, управление запасами и т.д. Для их решения используется линейное, нелинейное, целочисленное, динамическое программирование и другие аналитические методы. В нашем курсе этим методам не будет уделяться внимание.
Но есть задачи, которые этими методами не решаются. Прежде всего, это многокритериальные задачи в сложных ситуациях. То есть сложными будем считать ситуации, в которых есть несколько критериев, а также есть действия неопределённых факторов или необходимость учёта мнений нескольких лиц и т.д.
Как правило, не существует решения наилучшего по всем критериям, критерии часто бывают противоречивы. То есть выбрать надо оптимальное сочетание.
Центральное место в современной науке о принятии решений уделяется многокритериальным задачам выбора, так как в жизни чаще встречаются именно такие задачи.
Необходимо иметь в виду, что какого-либо формального математического метода «преодоления» многокритериальности не может быть в принципе. Все без исключения методы решения многокритериальных задач представляют собой различные способы организации взаимодействия с ЛПР и отличаются формой вопросов, которые ему «задаются» компьютерной программой.
Начинать надо с составления перечня целей, которые мы преследуем, решая задачу выбора. И только от него переходить к перечню критериев. Такая последовательность действий позволит контролировать соответствие формируемого списка критериев целям, которые мы преследуем, решая задачу. Эта последовательность действий естественно подталкивает к тому, чтобы рассмотреть альтернативные варианты критериев исходя из поставленных целей.
Упражнения
Решить ту же задачу для следующих таблиц с данными
Задание 1
| Критерий Альтернатива | 1-й | 2-й | 3-й |
| 1. | N | ||
| 2. | (m-1)*100 | ||
| 3. | |||
| 4. | (n+4)*100 | ||
| 5. | |||
| 6. | 11-n | 7+m |
Задание 2
| Критерий Альтернатива | 1-й | 2-й | 3-й |
| 1. | 4+n | ||
| 2. | 8+m | ||
| 3. | (10-m)*10 | ||
| 4. | 11-n |
Задание 3
| Критерий Альтернатива | 1-й | 2-й | 3-й | 4-й |
| 1. | 10-m | |||
| 2. | ||||
| 3. | (9-n)*1000 | |||
| 4. | 6+m | 10-m | ||
| 5. | 10-m | 12-n | ||
| 6. | 11-n | 2+m |
Задание 4
| Критерий Альтернатива | 1-й | 2-й | 3-й | 4-й |
| 1. | 10-m | |||
| 2. | ||||
| 3. |
Задание 5
| Критерий Альтернатива | 1-й | 2-й | 3-й | 4-й |
| 1. | ||||
| 2. | ||||
| 3. | 10-n | |||
| 4. | 3+m |
Задание 6
| Критерий Альтернатива | 1-й | 2-й | 3-й | 4-й | 5-й |
| 1. | |||||
| 2. | 2+n | ||||
| 3. | 10-n | 13-n | |||
| 4. | 17-n | 1+m |
Где n– первая цифра в номере студенческого билета, а m- вторая.
Выбор наилучшей альтернативы из оптимальных
Выделение множества Парето можно рассматривать лишь как предварительный этап оптимизации, и налицо проблема сокращения этого множества.
Предварительно необходимо провести нормализацию таблиц с оценками эффективных альтернатив. Нормализация может быть проведена, например, делением каждого значения критерия на максимальное по столбцу или на сумму всех значений этого критерия по всем альтернативам (по столбцу).
Нормализуем таблицу с оставшимися альтернативами из нашего примера
| Критерий Альтернатива | 1-й | 2-й | 3-й | 4-й | 5-й |
Первый способ нормализации:
| Критерий Альтернатива | 1-й | 2-й | 3-й | 4-й | 5-й |
| 9000/11000 | 8/9 | 5/10 | 8/10 | 4/9 | |
| 7000/11000 | 9/9 | 8/10 | 10/10 | 9/9 | |
| 4000/11000 | 2/9 | 10/10 | 6/10 | 8/9 | |
| 11000/11000 | 6/9 | 7/10 | 5/10 | 9/9 |
В итоге получаем следующую таблицу уже нормализованную
| Критерий Альтернатива | 1-й | 2-й | 3-й | 4-й | 5-й |
| 0,81 | 0,89 | 0,5 | 0,8 | 0,44 | |
| 0,64 | 0,8 | ||||
| 0,36 | 0,22 | 0,6 | 0,89 | ||
| 0,67 | 0,7 | 0,5 |
Второй способ нормализации:
| Критерий Альтернатива | 1-й | 2-й | 3-й | 4-й | 5-й |
| 9000/31000 | 8/25 | 5/30 | 8/29 | 4/30 | |
| 7000/31000 | 9/25 | 8/30 | 10/29 | 9/30 | |
| 4000/31000 | 2/25 | 10/30 | 6/29 | 8/30 | |
| 11000/31000 | 6/25 | 7/30 | 5/29 | 9/30 |
Делитель – это сумма столбца, в котором этот делитель используется.
В итоге получаем следующую уже нормализованную таблицу
| Критерий Альтернатива | 1-й | 2-й | 3-й | 4-й | 5-й |
| 0,29 | 0,32 | 0,17 | 0,28 | 0,13 | |
| 0,23 | 0,36 | 0,27 | 0,34 | 0,30 | |
| 0,13 | 0,08 | 0,33 | 0,21 | 0,27 | |
| 0,35 | 0,24 | 0,23 | 0,17 | 0,30 |
(Упражнения:Нормализуйте таблицы с оставшимися эффективными альтернативами из предыдущих шести заданий.)
Затем можно использовать различные принципы, одним из которых является принцип справедливой уступки.
Принцип справедливой уступки.
У этого принципа имеются следующие разновидности.
1. Принцип абсолютной уступки. Наилучшим считается решение, при котором суммарный абсолютный уровень снижения одного или нескольких критериев не превосходит суммарного абсолютного уровня повышения других.
2. Принцип относительной уступки. Наилучшим считается такое решение, при котором суммарный относительный уровень снижения одного или нескольких критериев не превосходит относительного суммарного уровня повышения по остальным критериям.
Рассмотрим решение нашего примера с использованием принципа абсолютной уступки. Последовательно найдём наилучшее решение: пусть наилучшим будет вторая альтернатива. В этом случае при сравнении с третьей мы должны получить, что у третьей альтернативы больше минусов, чем плюсов по сравнению со второй. Поверим так ли это: ухудшение на 0,06 при переходе к третьей есть только по первому критерию по всем остальным идёт улучшение, следовательно, наше предположение неверно и третья альтернатива лучше второй. Пусть тогда лучшей будет третья сравним её с пятой: пятая альтернатива лучше только по третьему критерию на 0,05, а по всем остальным она гораздо хуже, следовательно третья альтернатива лучше пятой. Осталось сравнить третью и шестую альтернативы. Шестая лучше по первому критерию на 0,12, а по второму, третьему и четвёртому хуже в сумме на 0,12+0,04+0,17=0,33, пятый критерий имеет одинаковые оценки, следовательно третья альтернатива лучше шестой и является наилучшей при применении принципа абсолютной уступки.
Ответ: наилучшей с применением принципа абсолютной уступки является третья альтернатива.
Практически можно находить наилучшую по этому принципу просто сложив нормализованные оценки по всем критериям для каждой альтернативы и выбрать ту, у которой эта суммарная оценка наивысшая.
В нашем примере альтернативы имеют следующие суммарные оценки
| Альтернатива | Суммарная оценка |
| 1,19 | |
| 1,5 | |
| 1,02 | |
| 1,29 |
Как видно наилучшая – третья альтернатива
Упражнения
Доделать предыдущие задания: найти наилучшее решение, используя принцип абсолютной уступки.
Этапы метода анализа иерархий
1. Очертить проблему и определить,что мы хотим
2. Построить иерархию ( цель, критерии, альтернативы)
3. Построить множество матриц парных сравнений для каждого из нижних уровней по одной матрице для каждого элемента примыкающего сверху уровня
4. Проверить индекс согласованности каждой матрицы
5. Использовать иерархический синтез для взвешивания собственных векторов
Иерархия строится следующим образом: сначала определяется цель принятия решения (фокус проблемы). Это высший уровень иерархии. Например, выбор наилучшего места работы, ВУЗа для учёбы и т.д. За фокусом следует уровень наиболее важных критериев (оплата труда, время, необходимое для проезда на работу, и т.д.). Каждый критерий может делиться на субкритерии. За субкритериями следует уровень альтернатив, число которых может быть достаточно большим. Декомпозиция проблемы в иерархию зависит от хода мысли ЛПР, его концепции решения проблемы, интуиции и опыта.
Рассмотрим упрощённую модель принятия решения о выборе места работы. Есть три места работы: А1, А2 и А3.
При выборе работы учитываются четыре критерия: зарплата (К1), удалённость от дома (К2), перспективы карьерного роста (К3) и риск потери работы (К4). 
Полученная иерархия соответствует 3-уровневой полной иерархии с фокусом принятие решения. Иерархия называется полной, если между элементами соседних уровней имеются все возможные связи.
Рассмотрим другую проблему – подбор кандидата на вакантное место: трёх кандидатов оценивают два эксперта, каждый по своим двум критериям, а затем докладывают свои выводы руководству для принятия окончательного решения. В этом случае иерархия будет выглядеть следующим образом.

Полученная иерархия соответствует 4-х уровневой неполной иерархии с фокусом ПР. Но её можно свести к набору из двух полных трёхуровневых иерархий и одной двухуровневой: для этого нужно разрезать связи между фокусом и элементами С1 и С2.
Первая иерархия даст в результате мнение первого эксперта о кандидатах.

Вторая иерархия даст в результате мнение второго эксперта о кандидатах.
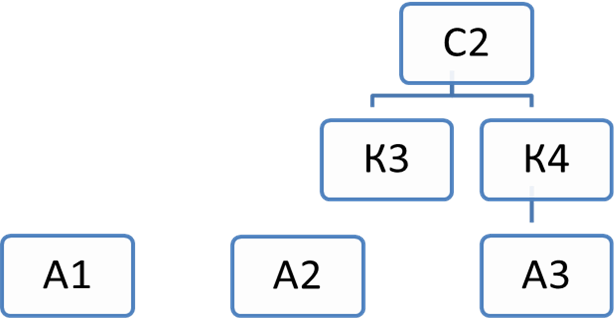
Последняя иерархия даст возможность руководителю принять окончательное решение, основываясь на мнениях экспертов и степени доверия каждому из них.
| ПР |
| С1 |
| А1 |
| А2 |
| А3 |
| С2 |
Вывод: анализ неполных иерархий можно свести к анализу набора соответствующих полных иерархий.
Одним из способов практического сравнения объектов, действий или обстоятельств для их количественной оценки является построение матрицы парных сравнений.
| А | В | С | … | |
| А | а11 | а12 | а13 | … |
| В | а21 | а22 | а23 | … |
| С | а31 | а32 | а33 | … |
| … | … | … | … | … |
В этой таблице а12–отношение важности объекта А по сравнению с В, а13- отношение важности объекта А по сравнению с С и т.д.
Матрица А называется обратносимметричной, если: 
Матрица А является согласованной, если: 
Собственным вектором матрицы A называется такой ненулевой вектор  , что для некоторого
, что для некоторого  :
: 
Собственным значением матрицы A называется такое число  , для которого существует собственный вектор
, для которого существует собственный вектор  , то есть уравнение
, то есть уравнение  имеет ненулевое решение .
имеет ненулевое решение .
Теорема. Положительная обратносимметричная матрица согласована тогда и только тогда, когда  ,где
,где  -максимальное собственное значение матрицы, а n-размерность матрицы (в нашем случае количество сравниваемых элементов).
-максимальное собственное значение матрицы, а n-размерность матрицы (в нашем случае количество сравниваемых элементов).
Для получения хороших результатов требуется использовать подходящую численную шкалу сравнений и определять степень несогласованности суждений.
Наиболее распространённой на сегодняшний день в методе анализа иерархий является следующая шкала:
· Если объект А и В одинаково важны, то их отношение записывается в виде 1:А/В=1 и В/А=1[1]
· Если А незначительно важнее В, то в качестве отношения А/В используют 3 (слабое предпочтение): А/В=3, В/А=1/3[2]
· Если А значительно важнее В – 5 (предпочтительнее): А/В=5, В/А=1/5
· Если А явно важнее В (сильное предпочтение) – 7: А/В=7, В/А=1/7
· Если А по своей значимости абсолютно предпочтительнее В – 9: А/В=9, В/А=1/9
Числа 2, 4, 6 и 8 используются для облегчения компромисса между оценками. Понятно, что каждый ЛПР имеет право на свои оценки даже в случае идентичного выбора (варианты решения и критерии совпадают, но отношение к ним у разных людей разное).
Проанализируем свойства идеальной матрицы парных сравнений (то есть все соотношения оценены идеально).
1. Для любого i справедливо аii=1(диагональный элемент, расположенный на пересечении i-ой строки и i-го столбца), так как это отношение элемента по важности к самому себе.
2. Для любых i и k справедливо равенство аki* аik=1.
3. Для любых i, k и l справедливо равенство аik* аkl=ail. Это отражает согласованностьопределения соотношения элементов (это означает, что, например, при сравнении элементов с третьим в третьей строке не должно получиться, что второй элемент лучше пятого, если из первой строки сравнения с первым элементом следует, что пятый лучше второго).
4. Столбец с весами элементов является собственным вектором матрицы попарных сравнений, с собственным значением l равным количеству сравниваемых элементов (n). Если обозначить матрицу А, столбец с весами w, то будет справедливо А*w =n*w.
Если матрица попарных сравнений строится не на точных измерениях, а на субъективных суждениях, то она, естественно, может отклоняться от идеальной. В этом случае у матрицы будет несколько собственных значений.
Для определения собственного значения lmax необходимо решить характеристическое (алгебраическое n-го порядка) уравнение
½А - lmax *Е½=0, где Е – единичная матрица с учётом соотношения lmax³n.
Это можно сделать в EXCEL, используя пункт Подбор параметра, расположенный во вкладке Данные в группе Работа с данными, кнопка «Анализ что, если».
Можно оценить отклонение от согласованности матрицы сравнений разностью  , разделенной на (n-1), так какдля проведения парных сравнений n объектов или действий требуется
, разделенной на (n-1), так какдля проведения парных сравнений n объектов или действий требуется  суждений о парных сравнениях.Выражение
суждений о парных сравнениях.Выражение  называется индексом согласованности (ИС).
называется индексом согласованности (ИС).
Насколько плоха согласованность для определенной задачи, можно оценить путем сравнения полученного нами значения величины  с её значением из случайных суждений при сравнении объектов или процессов и соответствующих обратных величин матрицы того же размера.
с её значением из случайных суждений при сравнении объектов или процессов и соответствующих обратных величин матрицы того же размера.
Индекс согласованности сгенерированной случайным образом по шкале от 1 до 9 обратносимметричной матрицы с соответствующими обратными величинами элементов, назовем случайным индексом (СИ).
В Национальной лаборатории Окриджа сгенерировали средние СИ для матриц порядка от 1 до 15 на базе 100 случайных выборок. Ниже представлены порядок матрицы и средние СИ,определенные так, как описано выше:
| 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. | 11. | 12. | 13. | 14. | 15. |
| 0,00 | 0,58 | 0,90 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 | 1,51 | 1,48 | 1,56 | 1,57 | 1,59 |
Отношение ИС к среднему СИ для матрицы того же порядка называется отношением согласованности (ОС).
Значение ОС, меньшее или равное 0,10, считают приемлемым. Для идеально согласованной матрицы ОС=0, так как ИС=0.
Если ОС>0,1, то имеется рассогласование элементов матрицы парных сравнений. И это характеризует уровень доверия к полученным результатам. Чем больше это отличие, тем меньше доверие. То есть необходимо вернуться к этапу экспертных парных сравнений и постараться устранить или уменьшить рассогласование за счёт более тщательной оценки результатов парных сравнений.
Рассогласованность матрицы парных сравнений может быть вызвана, по крайней мере, двумя факторами:
· личными качествами эксперта
· степенью неопределенности объекта оценки
Таким образом, эта модификация метода парных сравнений содержит внутренние инструменты позволяющие определить качество обрабатываемых данных и степень доверия к ним. Эта особенность данной методики выгодно отличает её от большинства обычно применяемых при исследовании методов.
Можно избежать многих проблем при рассогласовании матриц парного сравнения, если перед построением таблицы парного сравнения записать сравниваемые варианты в цепочку от наименее предпочтительного к наиболее предпочтительному варианту (или наоборот), что позволит наглядно видеть разницу.
Далее с найденным значением lmax следует определить решение w матричного уравнения
А*w =lmax*w, то есть собственный вектор матрицы А, который и будет определять веса элементов, для которых построена матрица парных сравнений. Полученные значения необходимо нормализовать.
Первый способ
1. Суммируем элементы каждой строки и записываем полученные результаты в столбец;
2. Складываем все элементы найденного столбца;
3. Делим каждый из элементов этого столбца на полученную сумму.
Второй способ
1. Суммируем элементы каждого столбца и записываем полученные результаты в столбец;
2. Заменяем каждый элемент полученного столбца на обратный ему;
3. Складываем элементы столбца из обратных величин;
4. Делим каждый из этих элементов на полученную сумму.
Третий способ
1. Суммируем элементы каждого столбца;
2. Делим элементы каждого столбца на их сумму;
3. Складываем элементы каждой строки полученной матрицы;
4. Записываем результаты в столбец;
5. Делим каждый из элементов последнего столбца на порядок исходной матрицы n.
Четвертый способ
1. Перемножаем элементы каждой строки и записываем полученные результаты в столбец;
2. Извлекаем корень n-ой степени из каждого элемента найденного столбца;
3. Складываем элементы этого столбца;
4. Делим каждый из этих элементов на полученную сумму.
Каждый из этих четырёх способов при применении к идеальной матрице парных сравнений приводит к одному и тому же точному результату.
В применении к обратносимметричной, но не согласованной матрице, ни один из предложенных способов уже не даёт собственного вектора, но при ОС меньшем 0,1, полученные значения достаточно близко подходят к значениям собственного вектора. То есть полученное значение будет приближённым, но вполне достаточным для оценки альтернатив и их ранжирования. Сложность вычислений возрастает с увеличением номера способа, но при этом возрастает и точность.
Подведём итоги: заключительная часть иерархического анализа связана с обработкой сформированных матриц парных сравнений. На основе теоретически точных алгоритмов метода анализа иерархий это производится в следующей последовательности:
· С помощью собственного значения lmax оценивается согласованность (степень непротиворечивости) матриц парных сравнений и в случае их приемлемой согласованности переходят к оценке весомости элементов иерархии (собственного вектора w) на основе этих матриц. Для случая плохой согласованности какой-то из матриц парных сравнений возвращаются на этап формирования этой матрицы и стараются устранить плохую согласованность элементов матрицы. Практически это всегда можно сделать, улучшив качество экспертной работы, в крайнем случае, можно рассмотреть несколько вариантов парных оценок.
· Проводится вычисление весов для элементов иерархии на основе матриц парных сравнений и итоговый расчёт весов альтернатив с учётом структуры иерархии (иногда итоговые веса называют рангами или рейтингами альтернатив).
· Общий вес альтернативы будет вычисляться следующим образом: нормированный вес по каждому критерию для заданной альтернативы умножается на нормированный вес самого критерия, а затем результаты складываются. Процесс вычисления общего веса альтернатив можно записать в матричной форме:
WА – ПР= WА – К * W К– ПР, где WА – ПР - вектор весов альтернатив относительно ПР, W К– ПР - вектор весов критериев относительно ПР, WА – К - матрица весов альтернатив по критериям. Эта формула легко обобщается на любое число уровней, в правой части появляются дополнительные множители, соответствующие ещё одному уровню.
Пример.
Рассмотрим задачу с выбором места работы, о которой мы говорили выше. Сформируем матрицу парных сравнений по первому критерию. Пусть этот критерий – размер оплаты труда. Пусть для трёх альтернатив он имеет следующие значения: А1 – 600 у.е., А2 – 2000у.е., А3 – 1200 у.е.
Предположим, что после беседы с ЛПР мы получили следующую матрицу парных сравнений альтернатив по первому критерию
| К1 | А1 | А2 | А3 |
| А1 | 1/9 | 1/7 | |
| А2 | |||
| А3 | 1/5 |
Из этой матрицы видно, что самой плохой является первая вакансия, вторая абсолютно предпочтительнее первой, а третья гораздо предпочтительнее первой по мнению ЛПР. Из второй строчки видно, что вторая вакансия просто предпочтительнее третьей по мнению принимающего решения.
Сначала решим точным методом в EXCEL. Вспомним функцию подбор параметра, которая даст возможность подобрать lmax.
Перенесём на лист EXCEL составленную матрицу парных сравнений. За начальное значение l примем 3,00 (с учётом размерности матрицы) и скопируем матрицу парных сравнения в свободную область листа. Заменим диагональные элементы матрицы (1) на формулу - (1 – ссылка на ячейку, где записано значение l (3)).Это и будет матрица(А - l*Е). Используем функцию МОПРЕД для нахождения определителя этой матрицы в отдельной ячейке листа, значение этой функции по определению собственного значения должно равняться 0, но так как матрица не является идеальной, то её собственное значение отклоняется от 3, и мы получим результат отличный от 0. Для нахождения истинного собственного значения воспользуемся возможностью EXCEL подобрать необходимое значение в формуле для получения заданного результата. Откроем вкладку Данные- Работа с данными - Анализ «что, если» - Подбор параметра. Зададим требования, чтобы в ячейке с вычисленным значением определителя получился 0, подбирать необходимо значение ячейки, в которой мы задали собственное значение матрицы равное 3. Необходимо помнить, что по диагонали матрицы, определитель которой считается, обязательно должны стоять формулы со ссылкой на ячейку, значение которой подбираем, иначе результат не будет найден. Дальше в отдельных ячейках посчитаем индекс согласованности и отношение согласованности для данной матрицы парных сравнений. Индекс согласованности для найденного значения l ИС=0,10423 – вычислялся по формуле (3.20843-3)/2 и отношение согласованности ОС=0.17971 (ИС делится на 0,58, которые взяты из таблицы случайных индексов, приведённой выше, для n=3).После вычислений получим следующую картинку в EXCEL.
| К1 | А1 | А2 | А3 |
| А1 | -2,21 | 0,11 | 0,14 |
| А2 | 9,00 | -2,21 | 5,00 |
| А3 | 7,00 | 0,20 | -2,21 |
| lмахl | 3,20843 | ||
| Определитель матрицы | 0,00045517 | ||
| ис | 0,10421471 | ||
| ос | 0,17968054 |
Отношение согласованности больше 0,1, то есть матрица плохо согласована. Улучшить согласованность матрицы в нашем случае можно взяв в качестве элементов матрицы отношения уровней зарплат для соответствующих мест работы.
| К1 | А1 | А2 | А3 |
| А1 | 1/3 | 1/2 | |
| А2 | 1,5 | ||
| А3 | 2/3 |
Элементы этой матрицы сложнее интерпретировать в рамках универсальной шкалы сравнений (в реальности зарплаты могут отличаться в несколько раз больше), но зато она идеально согласована. lmax=3, а нормированные веса для этой матрицы вычислим, например, первым упрощённым способом, он даст результат соответствующий точным методам, так как матрица идеально согласована. При сложении элементов строк получим следующий столбец
| К1 | Сумма |
| А1 | 1,83 |
| А2 | 5,5 |
| А3 | 3,66 |
Сложив полученные в столбце значения, получим 10,99, далее последовательно делим элементы на эту сумму и окончательно получаем вес вакансий по первому критерию.
| К1 | Вес |
| А1 | 0,167 |
| А2 | 0,500 |
| А3 | 0,333 |
Так как значения нормализованы, то их сумма, естественно, равна 1.
Можно попробовать использовать более взвешенную матрицу сравнений на основе универсальной шкалы
| К1 | А1 | А2 | А3 |
| А1 | 1/7 | 1/5 | |
| А2 | |||
| А3 | 1/3 |
Для этой матрицы lmax=3,006489, индексы согласованности ИС=0,0324 и ОС=0.05594, то есть близка к идеальной.
Вывод: для количественных критериев иногда лучше рассматривать их идеальные матрицы, а для качественных плохо согласованных оценок проводить уточнения у ЛПР соотношений значимости.
Предположим, что после проведения сравнений по всем четырём критериям для ЛПР, мы получили следующий набор весов(у каждого ЛПР этот набор должен быть свой, так как не существует двух абсолютно одинаковых людей)
| Вакансии | Зарплата | Близость к дому | Перспективы карьерного роста | Вероятность не потерять работу |
| А1 | 0,167 | 0,670 | 0,412 | 0,350 |
| А2 | 0,500 | 0,214 | 0,255 | 0,250 |
| А3 | 0,333 | 0, 116 | 0,333 | 0,400 |
После определения весов вакансий по отдельным критериям, необходимо определить отношения ЛПР к самим критериям, если все критерии имеют для ЛПР одинаковую важность, то для определения нужной вакансии достаточно сложить все веса этой вакансии. Но в жизни такой вариант практически не встречается. Кому-то важнее перспективы, кому-то зарплата, кому-то дорога, а кому-то стабильность. Да и соотношения между критериями могут отличаться. Предположим, что для ЛПР наиболее важным является стабильность (вероятность не потерять работу), близость к дому и зарплата имеют приблизительно одинаковое значение, а карьерный рост наименее значим. Точную таблицу, как в случае с зарплатой построить не удастся, положим, что после беседы с ЛПР была получена следующая матрица парных сравнений:
| Выбор работы | Зарплата | Близость к дому | Перспективы карьерного роста | Вероятность не потерять работу |
| Зарплата | 1/5 | |||
| Близость к дому | 1/5 | |||
| Перспективы карьерного роста | 1/3 | 1/3 | 1/7 | |
| Вероятность не потерять работу |
Проверим согласованность данной матрицы. За начальнуювеличину собственного значения в этом случае необходимо принять 4, а при определении отношения согласованности делитель из таблицы случайных индексов берётся для размерности 4 и равен 0,9. В результате получим следующее
| Выбор работы | Зарплата | Близость к дому | Перспективы карьерного роста | Вероятность не потерять работу |
| Зарплата | -3,07347 | 0,2 | ||
| Близость к дому | -3,07347 | 0,2 | ||
| Перспективы карьерного роста | 0,333333 | 0,333333 | -3,073466931 | 0,142857 |
| Вероятность не потерять работу | -3,07347 | |||
| Собственное значение | 4,073467 | Определитель | -4,4E-06 | |
| ИС | 0,024489 | |||
| ОС | 0,02721 |
Мы видим, что матрица достаточно хорошо согласована. Определим вес критериев для ЛПР. Для этого воспользуемся четвёртым из предложенных выше алгоритмов. Найдём произведение элементов каждого столбца и извлечём из полученных значений корень четвёртой степени. Резульат представлен ниже
| Выбор работы | Произведение | Корень четвёртой степени |
| Зарплата | 0,6 | 0,88 |
| Близость к дому | 0,6 | 0,88 |
| Перспективы карьерного роста | 0,159 | 0,35 |
| Вероятность не потерять работу | 3,64 |
Сложим элементы последнего столбца 5,75 и разделим корень четвёртой степени для каждого критерия на найденную сумму. Это и будет требуемый вес критериев.
| Выбор работы | Вес |
| Зарплата | 0,15 |
| Близость к дому | 0,15 |
| Перспективы карьерного роста | 0,07 |
| Вероятность не потерять работу | 0,63 |
Теперь можно окончательно определить вес каждой вакансии либо, воспользовавшись выше приведённой матричной формой, умножив матрицу с весами вакансий по критериям (результат обработки критериев см. выше) и последний полученный столбец, либо по формуле:
Вес вакансии = Вес вакансии по зарплате * Вес зарплаты + Вес вакансии по близости к дому * Вес близости к дому + Вес вакансии по перспективам * Вес перспектив + Вес вакансии по вероятности не потерять работу * Вес вероятности не потерять работу.
Посчитаем для первой вакансии
А1=0,167*0,15+0,670*0,15+0,412*0,07+0,35*0,63=0,375
Окончательно получим следующие веса
| Альтернативы | Общий вес |
| А1 | 0,374787 |
| А2 | 0,283051 |
| А3 | 0,342162 |
Ответ: Окончательно делаем вывод, что ЛПР должен выбрать первую вакансию с учётом своих предпочтений.
Выполнить следующие упражнения, пройдя все этапы метода анализа иерархий и выбрав наилучший вариант, как в выше изложенном примере.
Задание 1.
Определить город (или район в Вашем городе), наилучшим образом приспособленный к проживанию (у каждого человека могут быть свои предпочтения). Для решения задачи создать полную трёхуровневую иерархию, содержащую не менее трёх критериев, по которым идёт оценка (например, качество инфраструктуры, экология и т.д.), и не менее трёх вариантов для выбора.
Задание 2.
Определить вид физической нагрузки, наилучшим образом подходящий Вам для поддержания здоровья. Для решения задачи создать полную трёхуровневую иерархию, содержащую не менее трёх критериев, по которым идёт оценка (например, физическая нагрузка, насколько интересен лично Вам данный вид занятий и др.), и не менее трёх вариантов для выбора.
Задание 3.
Определить отношение согласованности для следующей матрицы парного сравнения
| А | В | С | |
| А | n | m | |
| В | 1/n | ||
| С | 1/m | 1/3 | |
|
Последнее изменение этой страницы: 2016-07-22 lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда... |