Элементарные математические модели

Рассмотрим некоторые подходы к построению простейших математических моделей, иллюстрирующие применение фундаментальных законов природы, вариационных принципов, аналогий, иерархических цепочек. Несмотря на простоту, привлекаемый материал даст возможность начать обсуждение таких понятий, как адекватность моделей, их "оснащение", нелинейность, численная реализация и ряда других принципиальных вопросов математического моделирования.

1. Фундаментальные законы природы. Наиболее распространенный метод построения моделей состоит в применении фундаментальных законов природы к конкретной ситуации. Эти законы общепризнанны, многократно подтверждены опытом, служат основой множества научно-технических достижений. Поэтому их обоснованность не вызывает сомнений, что, помимо всего прочего, обеспечивает исследователю мощную психологическую поддержку. На первый план выдвигаются вопросы, связанные с тем, какой закон (законы) следует применять в данном случае и как это делать.

а) Сохранение энергии. Этот закон известен почти двести лет и занимает, пожалуй, наиболее почетное место среди великих законов природы. Полагаясь на него, эксперт по баллистике, желающий быстро определить скорость револьверной пули и не имеющий поблизости специальной лаборатории, может воспользоваться относительно простым устройством типа маятника — груза, подвешенного на легком жестком и свободно вращающемся стержне (рис. 1.2).

Рис. 1.2.

Пуля, застрявшая в грузе, сообщит системе "пуля—груз" свою кинетическую энергию, которая в момент наибольшего отклонения стержня от вертикали полностью перейдет в потенциальную энергию системы.

Эти трансформации описываются цепочкой равенств .

Здесь 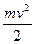— кинетическая энергия пули массы , имеющей скорость , — масса груза, — скорость системы "пуля—груз" сразу после столкновения, — ускорение свободного падения, — длина стержня, — угол наибольшего отклонения.

Искомая скорость определяется формулой

, (1)

которая будет вполне точной, если не учитываемые нами потери энергии на разогрев пули и груза, на преодоление сопротивления воздуха, разгон стержня и т. д. невелики. Это, на первый взгляд, разумное рассуждение на самом деле неверно. Процессы, происходящие при "слипании" пули и маятника, уже не являются чисто механическими. Поэтому примененный для вычисления величины закон сохранения механической энергии несправедлив: сохраняется полная, а не механическая энергия системы. Он дает лишь нижнюю границу для оценки скорости пули (для правильного решения этой простой задачи надо воспользоваться также законом сохранения импульса).

Сходные рассуждения может применить и для оценки времени 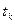сверления слоя металла толщины лазером с мощностью , излучение которого перпендикулярно поверхности материала (рис. 1.3).

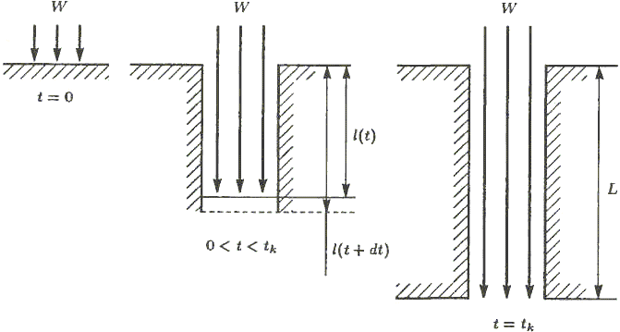
Рис. 1.3. Начальная, промежуточная и конечная стадии сверления металла лазером

Если энергия лазера полностью идет на испарение столбика металла массы 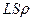( — облучаемая площадь, — объем столбика, — плотность вещества), то закон сохранения энергии выражается равенством

, (2)

где — энергия, требуемая для испарения единицы массы.

Величина имеет составную структуру: , поскольку материал необходимо последовательно нагреть до температуры плавления , а затем расплавить и превратить в пар ( — исходная температура, - удельная теплоемкость, и , — соответственно, удельная теплота плавления и парообразования).

Изменение глубины выемки со временем определяется из детального баланса энергии в промежутке времени от до . На испаренную за это время массу

тратится энергия , равная энергии , сообщаемой веществу лазером:

откуда получается дифференциальное уравнение

.

Его интегрирование (с учетом того, что начальная глубина выемки равна нулю) дает

, (3)

где — вся энергия, выделенная лазером к моменту времени . Следовательно, глубина выемки пропорциональна затраченной энергии (причем величина 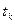, когда 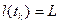, совпадает с вычисленной по формуле (2)).

б) Сохранение материи. Именно этим соображением руководствуется школьник, решающий задачу о заполнении бассейна водой, втекающей и вытекающей из двух труб. Конечно же, область применения этого закона несравненно шире.

Пусть, например, имеется небольшое количество радиоактивного вещества (урана), окруженного толстым слоем "обычного" материала (свинца), — ситуация типичная либо при хранении делящихся материалов, либо при их использовании в энергетике (рис. 1.4).

Рис. 1.4.

Под словом "небольшой" подразумевается упрощающее обстоятельство, а именно то, что все продукты распада, не испытывая столкновений с атомами вещества, беспрепятственно покидают область . Другими словами, длина свободного пробега продуктов распада в первом веществе значительно больше характерных размеров самого материала , т.е. 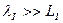. Слова "толстый слой" означают, что в согласии с целями хранения продукты деления полностью поглощаются в области II. Это гарантируется при выполнении противоположного условия 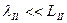, где — длина пробега продуктов распада во втором веществе, 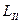— его характерный размер.

Итак, все, что вылетает из области I, поглощается в области II, и суммарная масса обоих веществ со временем не меняется. Это и есть закон сохранения материи, примененный к данной ситуации. Если в начальный момент времени 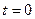массы веществ были равны M_I(0) и M_II(0), то в любой момент времени справедлив баланс

. (4)

Одного уравнения (4), очевидно, недостаточно для определения текущих значений двух масс - и . Для замыкания математической формулировки необходимо привлечь дополнительное соображение о характере распада. Оно гласит, что скорость распада (число атомов, распадающихся в единицу времени) пропорционально общему числу атомов радиоактивного вещества. За небольшое время 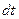между моментами и всего распадется

, , ,

атомов. Здесь вторично использован закон сохранения вещества, но применительно не ко всему процессу, а к отрезку времени 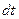. В этом уравнении, описывающем баланс атомов, в правой части стоит знак минус (вещество убывает), а величина отвечает некоторому среднему значению числа атомов за рассматриваемое время. Перепишем его в дифференциальной форме:

.

Учитывая, что 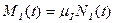, где 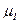— атомный вес вещества I, получаем

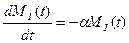. (5)

При самопроизвольной радиоактивности любой атом имеет некоторую не зависящую от состояния окружающего вещества вероятность распада. Поэтому чем больше (меньше) самого радиоактивного вещества, тем больше (меньше) выделяется продуктов распада в единицу времени. Коэффициент пропорциональности (постоянная распада) определяется конкретным веществом.

Уравнения (4), (5) вместе с условиями 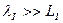, , а также величинами , , 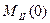и составляют математическую модель рассматриваемого объекта.

Интегрируя (5), получаем, что масса делящегося материала убывает по экспоненциальному закону

,

и при в области I вещество полностью исчезает.

Так как суммарная масса в соответствии с (4) остается постоянной, то в области II количество вещества растет:

,

и при продукты распада полностью переходят из области I в область II.

в) Сохранение импульса. Неподвижно стоящая в безветренную погоду на поверхности озера лодка начнет двигаться вперед, если сделать несколько шагов от ее носа к корме. Так проявляет себя закон сохранения импульса, утверждающий: полный импульс системы, не испытывающей действия внешних сил, сохраняется. На передвижение гребца лодка реагирует смещением в противоположную сторону.

Принцип реактивного движения положен в основу многих замечательных технических устройств, например, ракеты, выводящей на орбиту вокруг Земли искусственный спутник, для чего ей требуется развить скорость примерно 8 км/с. Простейшая математическая модель движения ракеты получается из закона сохранения импульса в пренебрежении сопротивлением воздуха, гравитацией и другими силами, исключая, конечно, тягу реактивных двигателей.

Пусть продукты сгорания ракетного топлива покидают расположенные в кормовой части выхлопные сопла со скоростью (для современных топлив величина и равна 3-5 км/с). За малый промежуток времени 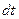между моментами и часть топлива выгорела, и масса ракеты изменилась на величину 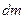. Изменился также импульс ракеты, однако суммарный импульс системы "ракета плюс продукты сгорания" остался тем же, что и в момент , т.е.

,

где — скорость ракеты, , - средняя за промежуток 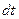скорость истекающих из сопел газов (обе скорости берутся относительно Земли). Первый член в правой части этого равенства - импульс ракеты в момент , второй — импульс, переданный истекающим газом за время .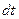

Учитывая, что , закон сохранения импульса можно переписать в виде дифференциального уравнения

,

в котором член , очевидно, не что иное, как сила тяги ракетных двигателей, и которое, будучи преобразованным к виду

,

легко интегрируется:

,

где , - соответственно скорость и масса ракеты в момент .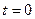

Если , то максимальная скорость ракеты, достигаемая при полном сгорании топлива, равна

(6)

Здесь 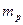- полезная масса (масса спутника), - структурная масса (масса собственно ракетной конструкции - топливных баков, двигателей, систем управления и т.д.).

Простая формула Циолковского (6) позволяет сделать фундаментальный вывод о конструкции ракеты для космических полетов.

Введем величину

,

которая характеризует при отношение структурной и начальной масс ракеты.

Тогда для практически реальных значений , км/с получаем при

км/с,

Отсюда следует, что даже в самой идеальной ситуации (полезная масса равна нулю, отсутствуют гравитация и сопротивление воздуха и т.д.) ракета рассматриваемого типа не способна достичь первой космической скорости. Тем самым необходимо использовать многоступенчатые ракеты - вывод, к которому пришли основоположники космонавтики.

Данный пример иллюстрирует также своего рода принцип "наибольшего благоприятствия", часто используемый на начальной стадии математического моделирования сложных объектов: если объект, поставленный в наилучшие условия, не в состоянии достичь требуемых характеристик, то надо изменить сам подход к объекту, либо смягчить требования к нему; если же требования в принципе достижимы, то следующие шаги связаны с исследованием влияния на объект дополнительных осложняющих факторов.

2. Вариационные принципы. Еще один подход к построению моделей, по своей широте и универсальности сопоставимый с возможностями, даваемыми фундаментальными законами, состоит в применении так называемых вариационных принципов. Они представляют собой весьма общие утверждения о рассматриваемом объекте (системе, явлении) и гласят, что из всех возможных вариантов его поведения (движения, эволюции) выбираются лишь те, которые удовлетворяют определенному условию. Обычно согласно этому условию некоторая связанная с объектом величина достигает экстремального значения при его переходе из одного состояния в другое.

Допустим, автомобиль, движущийся с постоянной скоростью , должен попасть из точки А в точку В и при этом коснуться некоторой прямой линии С (рис. 2.1).

Рис. 2.1. Различные траектории движения из точки А в точку В с касанием прямой С. Жирной линией выделен быстрейший путь

Водитель автомобиля очень торопится и выбирает из множества траекторий путь, требующий минимальных затрат времени. Представим затраченное время как функцию величины - угла между прямой и отрезком пути от точки А до прямой:

.

Здесь и - длины перпендикуляров, опущенных из точек А и В на прямую, - угол между прямой и отрезком пути из точки касания до точки В.

Условие экстремальности по аргументу означает, что

или

. (7)

Для любых значений справедливо равенство

,

где с — расстояние между проекциями точек А и В на прямую (одинаковое для всех траекторий).

Дифференцируя его, получаем соотношение

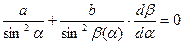, (8)

которое вместе с условием минимальности (7) означает

,

т.е. равенство углов и .

Далее нетрудно найти сами значения , через заданные величины а, b, с. Однако сейчас важно другое - условие минимальных затрат времени привело к выбору соответствующей траектории по правилу "угол падения равен углу отражения". Но ведь такому закону подчиняется и ход светового луча, попадающего на отражающую поверхность! Может быть, и в общем случае лучи света движутся по траекториям, обеспечивающим быстрейшее попадание сигнала из одной точки в другую? Да, именно так и происходит согласно известному вариационному принципу Ферма, опираясь на который, можно получить все основные законы геометрической оптики.

Покажем это, рассмотрев преломление лучей на границе двух сред (рис. 2.2).

Рис. 2.2

Свет, выходящий из точки А, движется в первой среде со скоростью 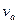, преломляется и, переходя через линию раздела, двигается во второй среде со скоростью и попадает в точку . Если — угол падения луча, а — угол его преломления, то время прохождения из в равно

Условие минимальности записывается в виде

,

а продифференцированное по условие постоянства величины 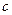по-прежнему выражается формулой (8).

Здесь величины а, b, с имеют тот же смысл, что и в предыдущем случае.

Исключая из последней формулы производную 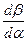, приходим к равенству

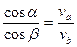, (9)

т.е. к известному закону преломления света.

Сформулированные применительно к какому-либо классу явлений вариационные принципы позволяют единообразно строить соответствующие математические модели. Их универсальность выражается также в том, что, используя их, можно в определенной степени отвлекаться от конкретной природы процесса. Так, водитель автомобиля, следующий принципу "минимального времени" и желающий попасть из точки А, находящейся на песчаной почве (одна скорость), в точку В, расположенную на травянистом лугу (другая скорость), обязан поехать не по прямой, соединяющей А и B, а по ломанной траектории, сделав необходимое "преломление" на линии, разделяющей песок и траву.

3. Применение аналогий при построении моделей. В огромном числе случаев при попытке построить модель какого-либо объекта либо невозможно прямо указать фундаментальные законы или вариационные принципы, которым он подчиняется, либо, с точки зрения наших сегодняшних знаний, вообще нет уверенности в существовании подобных законов, допускающих математическую формулировку. Одним из плодотворных подходов к такого рода объектам является использование аналогий с уже изученными явлениями. Что, казалось бы, общего между радиоактивным распадом и динамикой популяций, в частности изменением численности населения нашей планеты? Однако на простейшем уровне такая аналогия вполне просматривается, о чем свидетельствует одна из простейших моделей популяций, называемая моделью Мальтуса. В ее основу положено простое утверждение - скорость изменения населения со временем пропорциональна его текущей численности , умноженной на сумму коэффициентов рождаемости и смертности . В результате приходим к уравнению

, (10)

весьма похожему на уравнение радиоактивного распада и совпадающего с ним при 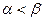(если и постоянные). Это неудивительно, так как при их выводе использовались одинаковые соображения. Интегрирование уравнения (10) дает

,

где — начальная численность.

На рис. 3.1 приведены графики функции при постоянных и (разным подобным друг другу кривым соответствуют разные — значения времени начала процесса). При численность остается постоянной, т.е. в этом случае решением уравнения является равновесная величина 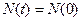. Равновесие между рождаемостью и смертностью неустойчиво в том смысле, что даже небольшое нарушение равенства приводит с течением времени ко все большему отклонению функции от равновесного значения . При 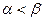численность населения убывает и стремится к нулю при 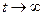, а при растет по некоторому экспоненциальному закону, обращаясь в бесконечность при 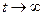. Последнее обстоятельство и послужило основанием для опасений Мальтуса о грядущем перенаселении Земли со всеми вытекающими отсюда последствиями.

Рис. 3.1. Изменение численности популяции со временем в модели Мальтуса

Как в данном примере, так и в ряде рассмотренных выше случаев можно указать немало очевидных ограничений применимости построенной модели. Конечно же, сложнейший процесс изменения численности населения, зависящий к тому же от сознательного вмешательства самих людей, не может описываться какими-либо простыми закономерностями. Даже в идеальном случае изолированной биологической популяции предложенная модель не отвечает реальности в полной мере хотя бы из-за ограниченности ресурсов, необходимых для ее существования. Сделанное замечание, тем не менее, нисколько не умаляет роли аналогий в построении математических моделей очень сложных явлений.

Применение аналогий основано на одном из важнейших свойств моделей - их универсальности, т. е. их увязке к объектам принципиально различной природы. Так, предположения типа "скорость изменения величины пропорциональна значению самой величины (или некоторой функции от нее)" широко используются в далеких друг от друга областях знаний.

4. Иерархический подход к получению моделей. Лишь в редких случаях бывает удобным и оправданным построение математических моделей даже относительно простых объектов сразу во всей полноте, с учетом всех факторов, существенных для его поведения. Поэтому естествен подход, реализующий принцип "от простого — к сложному", когда следующий шаг делается после достаточно подробного изучения не очень сложной модели. При этом возникает цепочка (иерархия) все более полных моделей, каждая из которых обобщает предыдущие, включая их в качестве частного случая.

Построим такую иерархическую цепочку на примере модели многоступенчатой ракеты. Как было установлено, реальная одноступенчатая ракета неспособна развить первую космическую скорость. Причина этого - затраты горючего на разгон ненужной, отработавшей части структурной массы. Следовательно, при движении ракеты необходимо периодически избавляться от балласта. В практической конструкции это означает, что ракета состоит из нескольких ступеней, отбрасываемых по мере их использования.

Пусть — общая масса ступени, - соответствующая структурная масса (при этом масса топлива равна величине ), 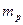- масса полезной нагрузки. Величины и скорость истечения газов одинаковы для всех ступеней. Возьмем для определенности число ступеней .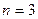

Начальная масса такой ракеты равна

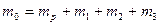
Рассмотрим момент, когда израсходовано все топливо первой ступени и масса ракеты равна величине

Тогда по формуле (6) первоначальной модели скорость ракеты равна

.

После достижения скорости 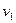структурная масса отбрасывается и включается вторая ступень. Масса ракеты в этот момент равна

Начиная с этого момента и до момента полного выгорания топлива второй ступени, ничто не мешает пользоваться уже построенной моделью, применив ее к рассматриваемому случаю. Все рассуждения о сохранении суммарного импульса и соответствующие выкладки остаются в силе (следует только учесть, что у ракеты уже есть начальная скорость ). Тогда по формуле (6) после выгорания топлива во второй ступени ракета достигает скорости

.

Такие же рассуждения применимы и к третьей ступени ракеты. После отключения ее двигателей скорость ракеты равна

.

Эту цепочку нетрудно продолжить для любого числа ступеней и получить соответствующие формулы. В случае же 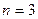для окончательной скорости имеем

,

или, вводя величины

, , ,

получаем

Данное выражение симметрично по отношению к величинам и нетрудно показать, что его максимум достигается в симметричном случае, т.е. при 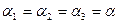.При этом для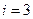

, .

Произведение , как легко проверить, равно отношению , или

.

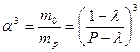Для многоступенчатой ракеты, аналогично, имеем

, , (11)

где — число ступеней.

Проанализируем формулу (11). Примем км/с, .

Тогда для получаем , , соответственно. Это значит, что двухступенчатая ракета пригодна для выведения на орбиту некоторой полезной массы (однако при одной тонне полезного груза необходимо иметь ракету весом 149 тонн). Переход к третьей ступени уменьшает массу ракеты почти в два раза (но, конечно же, усложняет ее конструкцию), а четырехступенчатая ракета не дает заметного выигрыша по сравнению с трехступенчатой.

Построение иерархической цепочки позволило относительно просто прийти к этим важным выводам. Иерархия математических моделей часто строится и по противоположному принципу "от сложного к простому". В этом случае реализуется путь "сверху вниз" - из достаточно общей и сложной модели при соответствующих упрощающих предположениях получается последовательность все более простых (но имеющих уменьшающуюся область применимости) моделей.

Лекция №2.