Уравнения звеньев и виды основных характеристик

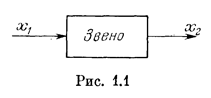
Чтобы составить уравнения динамики системы автома­тического управления или регулирования, система разби­вается на звенья (см. рис. В.4 и В.6). Затем рассматрива­ется каждое звено системы в отдельности (рис. 1.1). Входная и выходная величины соответствуют физи­ческим величинам, выражающим воздействие предыдуще­го звена на данное звено ( ) и воздействие данного звена на последующее ( ). Например, в электродвигателе следящей системы (см. рис. В.4) роль величины будет играть на­пряжение в цепи возбуждения, — угловая скорость вала. Для самолета (см. рис. В.6) — угол поворота руля, — отклонение оси самолета по курсу.

Звено системы может являться техническим устрой­ством любой физической природы, конструкции и назна­чения. Поэтому составление уравнения динамики каж­дого конкретного звена системы является предметом рас­смотрения соответствующей конкретной области техни­ческих наук (электротехники, теплотехники, динамики полета и т. п.), к которой и следует каждый раз обра­щаться.

Допустим, что в результате составления уравнения динамики какого-нибудь конкретного звена получилось линейное дифференциальное уравнение второго порядка

В теории автоматического регулирования принято приводить уравнение звена к стандартному виду в символической записи

где р обозначает операцию дифференцирования ( ).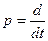

Здесь введены постоянные времени, которые в данном случае будут

и коэффициент усиления (передаточное число) звена

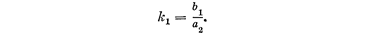
Очевидны следующие размерности этих постоянных:

В установившемся состоянии, когда = const и = const. получаем из (1.2) уравнение

и соответствующую ему линейную статическую характе­ристику звена (рис. 1.2), причем коэффициент усиления

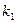определяет крутизну наклона этой характеристики ( 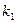=tg α с учетом размерностей и ). Условимся в дальнейшем на статических характеристиках писать крутизну 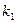(коэффициент усиления), как показано на рис. 1.2, б, вместо обозначения угла.

Линеаризация уравнения звена. В общем случае при составлении уравнения динамики звена системы оно ока­зывается нелинейным

Обычно при исследовании процесса регулирования уравнение звена можно линеаризовать (для тех случаев, когда этого сделать нельзя, используются методы теории нелинейных систем). Линеаризация уравнения динамики звена (1.3) основана на том, что в процессе регулиро­вания все величины мало отклоняются от их программ­ных значений — иначе система не выполнила бы своей задачи и не была бы системой регулирования или уп­равления.

Допустим, что установившиеся (программные) зна­чения переменных и являются постоянными , . Тогда можно записать

где символом А обозначены отклонения в процессе регу­лирования.

Из (1.3) можно записать уравнение звена в устано­вившемся состоянии

Разложив левую часть уравнения (1.3) в ряд Тей­лора, получим

где нуликом сверху обозначена подстановка ,0, ,0,0).

Вычитая из данного выражения уравнение (1.4) и отбросив все последующие члены разложения как малые высшего порядка, придем к линейному уравнению дина­мики звена в виде (1.1), если опустить значки Δ и по­нимать под х₁ и x₂ отклонения, причем

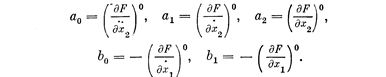
После этого можно перейти к стандартной записи (1.2).

Такому способу линеаризации поддаются те нелиней­ные уравнения, для которых возможно разложение в ряд Тейлора.

Линеаризацию уравнений можно производить и гра­фически, если имеется, например, зависимость F(x₁) при постоянном x₂ = и ₁ = ₂ = ₂ = 0 (рис. 1.3). Прове­дя касательную к заданной кривой F(x₁) в точке x₁⁰

найдем тангенс угла наклона касательной β, что с учетом масштабов даст значение коэффициента .

Аналогично, если задана нелинейная статическая ха­рактеристика звена x₂=f(x₁), ее можно линеаризовать путем проведения касательной (рис. 1.4), сведя таким образом к линейной (рис. 1.2).

Передаточная функция звена. Ее определение дается на базе преобразования Лапласа. Запишем преобразова­ния Лапласа для выходной и входной величин звена:

Пусть даны начальные условия

Тогда

Применив это преобразование к дифференциальному уравнению звена

получим

где через B(s) обозначен многочлен, включающий в себя все члены с величинами начальных условий.

Передаточной функцией звена W(s) называется отно­шение изображений Лапласа выходной и входной вели­чин, т. е.

при нулевых начальных условиях. В данном случае со­гласно (1.5) имеем

Сравнивая полученное выражение (1.7) с дифферен­циальным уравнением звена (1.2), видим, что формально передаточную функцию звена можно составлять как от­ношение операторных многочленов правой и левой частей уравнения звена. И наоборот, зная передаточную функ­цию (1.7) звена, легко написать его дифференциальное уравнение, имея в виду, что числитель передаточной функции соответствует правой части уравнения (1.2), а знаменатель передаточной функции (1.7) — левой части уравнения (1.2).

В общем случае передаточная функция звена имеет вид

где N(s) и L(s)—многочлены с коэффициентами 1 в младших членах, причем степень N(s), как правило, ниже степени L(s).

Дифференциальное уравнение звена. В общем случае в соответствии с (1.8) уравнение звена можно представить в форме

Характеристическое уравнение звена имеет вид

так что корни λ_i характеристического уравнения звена являются полюсами его передаточной функции.

Весовая функция звена. Весовой функцией звена k(t) называется оригинал (т. е. обратное преобразование Лапласа) передаточной функции, а именно:

где s_i—все полюса передаточной функции W(s). Иногда вместо k(t) применяют обозначение w(t). В этой фор­муле Res обозначает вычеты (см. теорию функций комплекс­ного переменного).

Поскольку при нулевых на­чальных условиях согласно (1.6)

то в случае, если Х₁ = 1, т. е. если х₁ (t) = δ (t) — дельта-функ­ция, будет иметь место ра­венство

Известно, что δ-функция представляет собой единичный мгновенный импульс (рис. 1.5),

для которого t₁ → 0, c₁ → ∞, причем площадь t₁ c₁ = 1.

Следовательно, физический смысл весовой функции звена есть реакция звена на единичный мгновенный импульс, поданный на вход звена.

Иначе говоря, весовая функция k(t) представляет собой переходный процесс на выходе звена (рис. 1.5) при подаче на его вход единичного импульса. Поэтому

весовую функцию часто называют импульсной переход­ной функцией.

Зная весовую функцию звена k (t), можно определить его передаточную функцию:

Переходная функция звена. Переходной функцией h(t) называется реакция звена на единичное ступенчатое воздействие (рис. 1.6), т. е. переходный процесс на вы­ходе х₂ при единичном скач­ке 1(t) на входе звена х₁.

Следовательно, здесь имеем

откуда

Поскольку известно, что (имея в виду обобщенные функции)

то можно написать следующее соотношение между весо­вой и переходной функциями звена:

Частотные характеристики звена. Частотными харак­теристиками называются формулы и графики, характе­ризующие реакцию звена на синусоидальное входное воздействие в установившемся режиме, т. е. вынужден­ные синусоидальные колебания звена.

Если на вход звена подается (рис. 1.7)

то на выходе будет (в установившемся режиме)

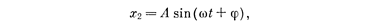
где А—амплитуда (точнее, усиление амплитуды), а φ— фаза (точнее, сдвиг по фазе).

Применяется символическая запись синусоидальных колебаний в виде

Строго говоря, е^jwt = cos ω + j sin ωt, что геометрически изображается вращающимся единичным вектором (рис. 1.8). Проекции последнего на прямоугольные оси

дают cos ωt и sin ωt. Поэтому для суждения о вынуж­денных синусоидальных колебаниях звена достаточно формально исследовать реакцию звена на символический сигнал е^jwt.

Пусть, например, уравнение звена имеет вид

Используем символическую запись:

Подставив эти величины в уравнение звена, получим

откуда

Сравнивая это выражение с передаточной функцией данного звена (1.7), видим, что

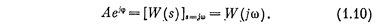
Отсюда находим

В общем виде согласно (1.8) имеем

Выражение (1.10) представляет амплитудно-фазовую частотную характеристику звена. Иногда W(jw) называ­ют частотной передаточной функцией звена. Выражения же (1.11) называются соответственно амплитудной ча­стотной характеристикой звена и фазовой частотной ха­рактеристикой звена.

Графически амплитудно-фазовая частотная характе­ристика (1.10) изображается на комплексной плоскости (рис. 1.9) в полярных координатах (A, φ), как годограф функции W(jw). Можно строить амплитудно-фазовую частотную характеристику и в прямоугольных координа­тах (U, V) (рис. 1.9), выделив в выражении W(jw) веществен­ную и мнимую части:

При этом U (ω) называют ве­щественной частотной характери­стикой, a v(ω)—мнимой.

Заметим, что угол φ показан на рис. 1.9 как отрицательный (отло­жен по часовой стрелке), посколь­ку чаще всего реакция на выходе звена имеет отставание по фазе по сравнению с входной величиной.

При этом частоту со изменяют от 0 до ∞ (сплошная кривая на рис. 1.9) или же от —∞ до +∞, когда добав­ляется еще симметричная к ней пунктирная кривая. Симметрия кривых при ω < 0 и ω > 0 объясняется тем, что передаточная функция W(s) согласно (1.8) есть от­ношение многочленов (дробно-рациональная функция). Поэтому

где чертой сверху обозначено комплексно-сопряженное выражение.

Графики амплитудной и фазовой частотных характе­ристик (1.11) тоже изображаются графически (рис. 1.10),

причем амплитуда являет­ся четной функцией, т. е. А(-ω)==A(ω), а фаза — нечетной функцией, т. е. φ(-ω)= -φ(ω).

Логарифмические частот­ные характеристики. В прак­тических применениях чаще всего амплитудную и фазо­вую частотные характеристи­ки изображают в логарифми­ческом масштабе. Впослед­ствии увидим, что такие логарифмические частотные ха­рактеристики очень удобны для инженерных расчетов.

При построении логарифмической амплитудной час­тотной характеристики (ЛАХ) по оси ординат откладыва­ют величину

единицей измерения для которой является децибел. По оси абсцисс откладывается частота 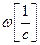в логарифми­ческом масштабе (рис. 1.11). Равномерной единицей на оси абсцисс является декада — любой отрезок, на кото­ром значение частоты со увеличивается в десять раз. Точка пересечения ЛАХ с осью абсцисс называется час­тотой среза .

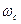Начало координат обычно помещают в точке ω = 1, так как lg 1 = 0. Точка же ω = 0 лежит в —∞. Однако в зависимости от интересующего вас диапазона частот можно начало координат брать в другой точке (ω ==0,1;

ω == 10 или др.). Важно иметь в виду, что ось абсцисс (Lm==0) согласно (1.12) соответствует значению А = 1, т. е. прохождению амплитуды сигнала через звено в на­туральную величину. Верхняя полуплоскость ЛАХ соот­ветствует значениям А > 1 (усиление амплитуды), а ниж­няя полуплоскость — значениям А < 1 (ослабление амплитуды).

При построении логарифмической фазовой частотной характеристики (ЛФХ) отсчет углов φ идет по оси орди­нат в обычном масштабе в угловых градусах (рис. 1.11). По оси абсцисс откладывается по-прежнему частота ω в логарифмическом масштабе.

Между частотными характеристиками и весовой функ­цией существуют соотношения, определяемые из (1.9) подстановкой s = jω, а именно:

Эти формулы представляют собой известные преобразо­вания Фурье.

Как видим, все рассмотренные виды динамических характеристик звеньев (передаточная функция, диффе­ренциальное уравнение, весовая функция, переходная функция, амплитудно-фазовая частотная характеристика) связаны между собой определенными зависимостями. Поэтому все они эквивалентны друг другу в определении динамических свойств звена системы управления.