Понятие устойчивости линеаризованных систем

Устойчивость систем автоматического управления яв­ляется одним из важнейших условий ее работоспособно­сти,, так как устойчивость включает в себя требование затухания переходных процессов во времени. Очевидно, что система с расходящимся процессом была бы нерабо­тоспособной

Все реальные системы в технике и в природе, как правило, являются в большей или меньшей степени не­линейными. Всегда существует много факторов, откло­няющих реальные характеристики от прямолинейных. Однако многие системы можно считать близкими к линейным и с необходимой для практики точностью про­ектировать как линейные. Для этого производится линеа­ризация характеристик и уравнений для реальных звень­ев системы (см. § 1.1).

Большое практическое значение имеют, конечно, и существенно нелинейные системы. Они рассматриваются отдельно в другом учебном пособии.

Итак, обратимся к линейным системам, рассматривая их как результат линеаризации реальных систем, т. е. к линеаризованным системам. Можно сказать, что линей­ная система является идеализированной (приближенной) математической моделью реальной системы.

Рассмотрим сначала идеально линейную систему. Под устойчивостью линейной системы понимают свойство за­тухания переходного процесса с течением времени, иначе говоря,— следующее свойство собственного (свободного) движения системы:

Из формул (3.5) для случая разных корней и (3.6) при наличии кратных корней характеристического урав­нения системы видно, что свойство (4.1) имеет место тогда и только тогда, когда все корни λ_i (i = 1, 2, ..., n) обладают отрицательными вещественными частями. Это иллюстрируется графиками для составляющих решения, соответствующих вещественному корню и паре комплекс­ных корней (рис. 4.1).

Если же хотя бы один вещественный корень λ_i харак­теристического уравнения будет положительным, или ес­ли хотя бы одна пара комплексных корней будет иметь

положительную вещественную часть, то переходный про­цесс будет расходящимся (рис. 4.2).

Если в характеристическом уравнении системы имеет­ся хотя бы один нулевой корень (λ_i=0) или хотя бы одна пара чисто мнимых корней(λ_i,i+1=0), а все ос­тальные корни имеют отрицательные вещественные ча­сти, то будем говорить, что система находится на гра­нице устойчивости. Это следует из того, что нулевой корень можно рассматривать как границу между отрица­тельным и положительным, а чисто мнимый корень — как границу между комплексными корнями с отрицатель­ной и положительной вещественными частями.

Поведением замкнутой системы на границе устойчи­вости пока интересоваться не будем, так как работоспо­собная система автоматического регулирования должна быть устойчивой с запасом и не приближаться к этой границе.

Условие устойчивости линейной системы выражается, следовательно, в том, что все корни характеристического уравнения λ_i должны располагаться в левой полупло­скости комплексного переменного λ (рис. 4.3). Мни­мая ось ω плоскости корней служит границей устой­чивости.

Можно выделить три типа границ устойчивости ли­нейной системы, которые характеризуются соответст­венно:

1) нулевым корнем λ₁ == 0;

2) парой чисто мнимых корней λ_1,2 = ±jω;

3) бесконечно удаленным корнем λ₁ = ∞. Заметим, что бесконечность на комплексной плоскости рассматривается как бесконечно удаленная точка, проти­воположная нулевой. Поэтому она тоже является гра­ницей между положительной (правой) и отрицательной (левой) полуплоскостями.

В первом случае (λ₁ = 0) граница устойчивости на­зывается апериодической, а во втором случае (λ_1,2 = ±jω)—колебательной, причем значение мнимой части

корня к» равно частоте незату­хающих колебаний системы на границе устойчивости, так как при λ_1,2 = ±jω имеем решение

где Лир определяются началь­ными условиями.

Перейдем теперь к реаль­ным системам, которые иссле­дуются в линеаризованном виде.

Прежде всего, надо дать общее определение понятия

устойчивости и определить, как может влиять на устой­чивость небольшое отличие реальной системы от ее ли­нейной математической модели. Надо быть уверенным, что исследование устойчивости проектируемой линейной системы обеспечит затем устойчивость и системы реаль­ной с малыми нелинейностями.

Общее определение понятия устойчивости любой ди­намической системы по Ляпунову выглядит следующим образом.

Запишем уравнения динамики нелинейной системы п-го порядка в нормальной форме Коши

при отсутствии возмущающих воздействий. Устойчивость рассматривается как свойство свободного движения си­стемы после начального отклонения ее, вызванного лю­быми причинами.

Пусть y*(t) обозначает некоторый установившийся процесс работы системы или, как говорят, невозмущенное движение. Отклонение возмущенного движения y(t), оп­ределяемого уравнениями (4.2) при начальных условиях у(t₀), обозначим через x(t):

Тогда можно написать уравнения возмущенного дви­жения в отклонениях в виде

а невозмущенное движение будет x* = 0. Переменные x_i являются координатами состояния системы (см. § 2.3).

В общем случае конкретное выражение уравнений (4.4) зависит от вида установившегося процесса y*(t), так как они получаются из (4.2) подстановкой (4.3). Поэтому, исследуя уравнения (4.4), вообще говоря, не­обходимо указывать, об устойчивости какого устано­вившегося режима или невозмущенного движения y*(t) идет речь.

Невозмущенное (установившееся) движение y^*_i(t) системы п-то порядка можно представить геометрически условно в n-мерном пространстве (с добавлением еще оси времени t) в виде некоторой кривой (рис. 4.4). Возму­щенное движение y(t), вызванное начальным отклонени­ем при t = t₀ изобразится другой кривой (рис. 4.4).

В отклонениях x(t), т. е. в пространстве координат состояния системы, эта кривая возмущенного движения будет выглядеть как показано на рис. 4.5. При этом невозмущенное движение х* = 0 изобразится прямой ли­нией, совпадающей с осью t.

Невозмущенное движение системы х* == 0 называется устойчивым, если, задав трубку сколь угодно малого n-мерного сечения ε (рис. 4.5), можно подобрать в на­чальный момент t₀ такую область начальных условий δ, зависящую от ε, что в дальнейшем с увеличением t воз­мущенное движение x(t) не выйдет из заданной трубки ε.

Аналитическое определение понятия устойчивости по Ляпунову формулируется следующим образом.

Невозмущенное движение системы х* = 0 называется устойчивым, если при заданном ε>0, сколь бы оно мало

ни было, существует такое δ > 0, зависящее от ε, что при начальных условиях

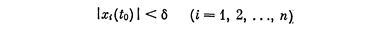
в дальнейшем движении (t₀ < t < ∞) будет все время соблюдаться условие

Заметим, что в этом аналитическом определении об­ласти ε и δ, в отличие от рис. 4.5, выглядят «прямо­угольными» (в n-мерном пространстве), что не имеет принципиального значения.

Невозмущенное движение х*=0 будет неустойчивым, если указанное условие не выполняется хотя бы для од­ного из x_i.

Если в рамках указанного выше условия имеем x(t)→0 при t→∞, то невозмущенное движение х*=0 на­зывается асимптотически устойчивым.

Если же х(t)→0 при t→∞ после любых больших начальных отклонений, то система называется устойчивой в целом (или «в большом»).

Обратимся теперь к линеаризованной системе. Урав­нения (4.4) в процессе линеаризации (разложением в ряд Тейлора) получают вид

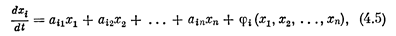
где через φ_i обозначены члены высокого порядка, начи­ная со второго.

Получаемая отсюда линейная система путем отбрасы­вания малых нелинейностей φ_i , называется первым при­ближением:

Для него можно написать характеристическое урав­нение

Для нелинейных систем, к которым применимо раз­ложение вида (4.5), существуют следующие три теоре­мы Ляпунова об исследовании устойчивости по первому приближению:

1) невозмущенное движение x* = 0 устойчиво незави­симо от вида малых нелинейностей φ_i если все корни характеристического уравнения D(λ)=0 имеют отрица­тельные вещественные части;

2) невозмущенное движение х* = 0 неустойчиво неза­висимо от вида малых нелинейностей φ_i если хотя бы один корень характеристического уравнения D(λ)=0 имеет положительную вещественную часть;

3) в случае наличия в каких-либо корнях характери­стического уравнения D(λ)=0 нулевой вещественной ча­сти при всех остальных отрицательных, ничего нельзя сказать об устойчивости невозмущенного движения х*=0 по первому приближению без специального исследо­вания полного уравнения (4.5) с малыми нелинейностями φ_i.

Третий случай для линейной теории автоматического управления не представляет интереса, так как наличие нулевого корня или чисто мнимых корней характеристи­ческого уравнения будет означать просто границу устой­чивости линейной системы. А система не должна находиться не только на границе устойчивости, но даже и вблизи нее.

Поэтому для наших целей достаточно использовать первые две теоремы, которые и являются обоснованием всей излагаемой ниже теории устойчивости линеаризованных систем, основанной на требовании к корням ха­рактеристического уравнения, указанном в начале дан­ного параграфа.

Заметим, что поскольку требование к корням обеспе­чивает свойство x_соб(t)→0 при t→∞ при любых на­чальных условиях, то линейная система оказывается всегда при этом устойчивой асимптотически и в целом («в большом»). Речь идет, конечно, об обыкновенных ли­нейных системах с постоянными параметрами.