Алгебраические критерии устойчивости

Выше было сформулировано условие устойчивости ли­нейной системы в виде требования к корням характери­стического уравнения. Однако вычисление корней урав­нения высокой степени затруднительно. Поэтому были выведены критерии устойчивости, позволяющие судить об устойчивости или неустойчивости системы непосредствен­но по коэффициентам характеристического уравнения без вычисления его корней.

Различные формы таких критериев рассматриваются в курсах высшей алгебры. В теории автоматического ре­гулирования наибольшее применение из алгебраических критериев устойчивости получили критерий Рауса и кри­терий Гурвица. Мы ограничимся одним последним.

Предварительно рассмотрим необходимое условие ус­тойчивости.

Пусть характеристическое уравнение линейной систе­мы D(λ)= 0 в развернутой форме имеет вид

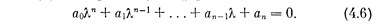
Докажем, что необходимым условием устойчивости яв­ляется положительность всех коэффициентов характери­стического уравнения, т. е.

(этому условию удовлетворяет и случай всех отрицатель­ных коэффициентов, если a₀ < 0, так как можно поме­нять все знаки на обратные).

Для доказательства разложим левую часть характе­ристического уравнения (4.0) на множители:

Пусть все корни его имеют отрицательные веществен­ные части

Поскольку средние два сомножителя дают

то видно, что после перемножения всех скобок получим в уравнении только положительные коэффициенты. Это и требовалось доказать.

Однако в общем случае положительность коэффици­ентов уравнения недостаточна для устойчивости системы. В самом деле, положительные коэффициенты уравнения могут получиться и при положительных вещественных частях комплексных корней. Но все вещественные корни при положительных коэффициентах уравнения будут обя­зательно отрицательными.

Только в частных случаях, когда имеется уравнение первой или второй степени, положительность коэффици­ентов оказывается необходимым и достаточным условием устойчивости (это легко проверить). А при п ≥ 3 это условие лишь необходимо, но недостаточно, ибо оно обес­печивает отрицательность только вещественных корней.

Приведем теперь критерий устойчивости Гурвица без доказательства. Он формулируется следующим образом.

Для устойчивости линейной системы необходимо и до­статочно, чтобы были положительными п главных опре­делителей следующей матрицы коэффициентов характе­ристического уравнения (4.6) данной системы:

В первой строке матрицы пишутся коэффициенты с нечетными индексами, во второй — с четными. Концы строк заполняются нулями, так чтобы матрица имела п столбцов, где п — порядок уравнения системы. Третья и четвертая строки получаются сдвигом первых двух на одно место вправо и т. д.

Указанные главные определители имеют вид

Они называются определителями Гурвица.

Последний определитель Гурвица, как видно из при­веденной выше матрицы, равен

Поэтому его положительность сводится при Δ _n-1 > 0 к условию a_i > 0.

Наиболее важным, как увидим далее, является пред­последний определитель Гурвица

Δ _n-1 > 0.

Для систем первого и второго порядка критерий Гур­вица сводится просто к положительности коэффициентов a₀, a₁ , a₂. Для системы третьего порядка характеристиче­ское уравнение имеет вид

а условие устойчивости по Гурвицу будет

причем остальные неравенства сводятся к требованию положительности коэффициентов a₀, a_1, a₂ , a₃. Условие (4.9) записывается еще в виде

(произведение средних коэффициентов уравнения должно быть больше произведения крайних). Этот критерий для систем третьего порядка ранее был получен И. А. Вышнеградским.

Аналогично для системы четвертого порядка

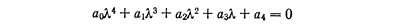
условием устойчивости по Гурвицу будет положитель­ность всех коэффициентов характеристического уравнения и выполнение неравенства

Для устойчивости систем пятого и шестого порядков требуется, кроме положительности коэффициентов, вы­полнение двух неравенств типа (4.9), (4.11), но более сложной формы. Для систем седьмого и восьмого поряд­ков — трех неравенств и т. д. Сложность этих неравенств быстро возрастает с увеличением порядка системы п.

Поэтому для общих исследований особенно удобен критерий Гурвица при п ≤ 4. Но при числовом задании всех коэффициентов легко проверить устойчивость систе­мы, конечно, и при любом п.

Найдем границы устойчивости. Апериодическая гра­ница устойчивости (нулевой корень) будет согласно урав­нению (4.6) в том случае, когда а_n = 0, но при условии положительности всех определителей Гурвица (кроме по­следнего) .

Пара чисто мнимых корней в характеристическом уравнении (колебательная граница устойчивости) появ­ляется при

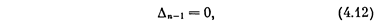
если при этом все остальные определители Гурвица по­ложительны (для систем третьего и четвертого порядка это последнее означает просто положительность коэффи­циентов уравнения).

Наконец, граница устойчивости, соответствующая бе­сконечному корню, будет, согласно уравнению (4.6), при a₀ = 0. В самом деле, если все уравнение разделить на λ ⁿ, то получим

Отсюда видно, что при а₀ = 0 имеем = 0, а значит λ = ∞.

Пример. Передаточная функция разомкнутой цепи си­стемы задана в виде (см. рис. 3.5):

Характеристическое уравнение замкнутой системы со­гласно § 2.3 будет

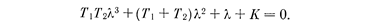
Коэффициенты его положительны. Условие устойчиво­сти но критерию Гурвица (4.1.0) получит вид

Эти три границы устойчивости можно изобразить гра­фически в пространстве параметров K , T₁ ,T₂ и найти области устойчивости системы.

Найдем сначала область устойчивости системы по од­ному параметру К (общий коэффициент усиления ра­зомкнутой цени). Пространство параметров здесь одна

прямая линия, а границы устойчивости — точки на ней:

К = 0 и К = К _гр (рис. 4.6). Область устойчивости соглас­но (4.13) лежит между этими точками.

Те же границы устойчивости системы можно постро­ить на плоскости двух параметров, например: К, Т₁ . Первая граница (К = 0) лежит на оси Т₁ (рис. 4.7). Вторая граница имеет вид гиперболы с асимптотами Т₁ = 0 и К = . Третья граница (Т₁ = 0) совпадает с осью К .

Область устойчивости, определяемая неравенством (4.13), обозначена на рис. 4.7. Штриховка границ дела­ется в сторону области устойчивости.

Как видим, при увеличении постоянных времени Т₁ , Т₂ область устойчивости сужается. Отрицательно влияет на устойчивость также и увеличение коэффициента уси­ления К. При любых заданных Т₁и Т₂ существует свое K _гр (рис. 4.6), после чего система становится неустойчи­вой. Это очень важное обстоятельство, так как мы знаем

(см. главу 3), что для повышения точности регулирова­ния необходимо увеличивать К. Тут выявляется противо­речие между требованием точности (увеличение К) и ус­тойчивости (ограничение К).

Далее можно построить область устойчивости и в про­странстве трех параметров К, Т₁ , Т₂ (рис. 4.8). Там жир­ной линией обозначена граница устойчивости, перенесен­ная с рис. 4.7. Границами устойчивости здесь являются три координатные плоскости и криволинейная поверх­ность, сечениями которой в вертикальных плоскостях, параллельных КОТ₁ и в горизонтальных, параллельных КОТ₂ , будут гиперболы.