Частотный метод синтеза корректирующих устройств

Наиболее распространен частотный метод синтеза корректирующих устройств с помощью логарифмических частотных характеристик. Он проводится следующим образом. Строится желаемая логарифмическая амплитуд­ная частотная характеристика, исходя из требуемой точ­ности системы и требуемого качества переходного про­цесса. Эта желаемая характеристика сравнивается с той, которую данная система имеет без коррекции. Определя­ется передаточная функция корректирующего устройства так, чтобы при его включении в систему, в последней получилась бы желаемая форма логарифмической ампли­тудной характеристики. Затем строится фазовая частот­ная характеристика и оценивается получающаяся при этом величина запаса устойчивости системы и другие качественные показатели.

Рассмотрим формирование желаемой логарифмической амплитудной частотной характеристики, исходя из задан­ных требований к системе по точности и качеству пере­ходного процесса.

Требования точности системы. Они формулируются по-разному.

1. Пусть даны «рабочие» частота ω_р и амплитуда a_p, т. е. основные значения частоты и амплитуды задающего воздействия g(t), которые будут иметь место при работе данной системы; задана также допустимая ошибка A_ε = ε_доп (амплитуда ошибки).

Для области низких частот, где |W( jω)| >> 1 можно записать

Следовательно, аналогично формуле (3.24) здесь мож­но записать

2. Пусть даны требуемые характеристики задающего воздействия: и , а также ε_{доп .}

Для использования частотных характеристик полагаем

где индексом р обозначены «рабочие» амплитуды и ча­стота, при которых будут иметь место заданные скорость и ускорение .

Тогда, пользуясь формулами (3.23), вычисляем

Заметим, что если g(t) является угловой величиной, то обычно пользуются следующими обозначениями:

Тогда вычисляются

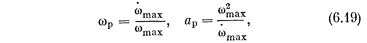
и желаемое значение |W(jω_p)| — по формуле (6.17).

3. Пусть в астатической системе требуется обеспечить слежение за сигналом g =

Имеем выражения

Коэффициенты ошибок

Установившаяся ошибка представляется в виде

или в других обозначениях

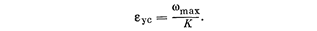
Отсюда находим желаемое значение

По этим данным, отражающим требования точности системы, строим низкочастотную часть желаемой лога­рифмической амплитудной частотной характеристики, как показано на рис. 6.15.

Начальный наклон характе­ристики —20 дБ/дек (астатизм 1-го порядка). Точка излома и дальнейший наклон пока еще не определены.

Требования качества пе­реходного процесса. Пусть заданы допустимое перерегулирование σ и время зату­хания переходного процесса t_п.

Воспользуемся графиком рис. 6.16, взятым из § 5.2.

По этому графику, отложив заданную величину σ (на­пример, 20%), определяем величину t_п (как показано стрелками на рис. 6.16), например

Но поскольку желаемое значение t_п нам задано, то можно вычислить необходимую частоту среза

Наносим найденное значение ω_с на график искомой желаемой ЛАХ (рис. 6.17) и проводим через точку ω_с прямую с наклоном —20 дБ/дек. Это реко­мендуется (см. § 5.2) для обеспечения хоро­шего качества переход­ного процесса.

Затем из предыдуще­го расчета берем низко­частотную часть харак­теристики и указанные части характеристики сопрягаем наклонной прямой с наклоном

—40 или —60 дБ/дек (рис. 6.17), как удоб­нее.

Высокочастотная часть заметной роли не играет. Поэтому ее берем такой, какая в данной системе имеется. Проверяем наличие не­обходимого запаса устойчивости по амплитуде ΔLm и по фазе Δφ (рис. 6.17).

Рассмотрим сначала синтез последовательного коррек­тирующего устройства, а затем параллельного.

Задана передаточная функция разомкнутой цепи си­стемы без коррекции W₀(s) (рис. 6.18). Соответствую­щая ей частотная характеристика отличается от желае­мой. Введем последовательное корректирующее устрой­ство с искомой передаточной функцией k_пП(s) (рис. 6.18).

Согласно описанной выше методике, строим желае­мую логарифмическую амплитудную частотную характе­ристику (рис. 6.17). Пусть коэффициент усиления же­лаемой системы K_ж. отличается от имеющегося К₀. Тогда нужно поднять характеристику W₀(jω) (рис. 6.19) так, чтобы на ней получился желаемый коэффициент усиления. Получаем новую характеристику

Расстояние между w₀^` и W₀ по вертикали в логариф­мическом масштабе и дает нам искомую величину

20 1gk_п , т. е. искомый коэффициент усиления корректи­рующего устройства

Теперь надо найти передаточную функцию корректи­рующего устройства П(s). Для этого совмещаем на один

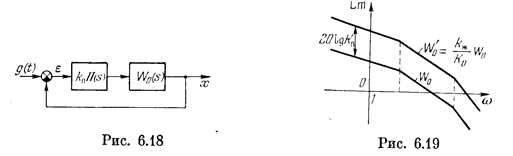
график логарифмические амплитудные частотные харак­теристики для W_ж и W₀^`. Они отличаются на участке от точки 1/T₁ до точки 1/Т₄ (рис. 6.20).

Поскольку требуется

то можно записать (после подстановки s = jω) следую­щее:

Следовательно, чтобы найти характеристику Lm(ω) для П(s), нужно вычесть характеристику Lm(ω) для

w₀^` из W_ж . Результат вычитания показан штрих пунктирной линией на рис. 6.20. Отсюда очевидна искомая пере­даточная функция последовательного корректирующего устройства

В заключение нужно построить фазовую характери­стику φ(ω) для W_ж и оценить запасы устойчивости (рис. 6.20).

По найденной передаточной функции можно соста­вить электрическую схему корректирующего устройства (см., например, [45]).

Перейдем к синтезу параллельного корректирующего устройства в виде дополнитель­ной обратной связи.

Задана передаточная функ­ция разомкнутой цепи W₀(s). Требуется ввести корректирую­щую обратную связь Z(s) так, чтобы система в целом (рис. 6.21) обладала желаемой частотной ха­рактеристикой.

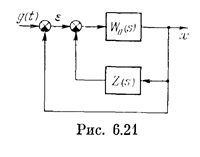Передаточная функция разомкнутой цепи с коррек­цией равна

Чтобы избавиться от суммы под знаком логарифма, запишем приближенно

Построим заданную логарифмическую характеристи­ку W₀ с желаемым коэффициентом усиления и желае­мую характеристику W_ж (рис. 6.22).

В качестве искомой характеристики 1/Z примем ха­рактеристику, обозначенную на рис. 6.22 точечным пунк­тиром и совпадающую в средней части с W_ж. Вычтем 1/Z из характеристики W₀. Получим

Этот результат показан па рис. 6.22 штрих пунктирной линией. Из графика видно, что на участке CD характе­ристика |ZW₀| > 1, а до точки С и после точки D харак­теристика |ZW₀|<1, так как ось абсцисс соответствует значению амплитуды, равному 1 (20 1gA = 0).

Следовательно, при принятом очертании искомой ха­рактеристики 1/Z удовлетворяются написанные выше приближенные равенства (6.23).

Таким образом, найдено параллельное корректирую­щее устройство в виде обратной связи, которое создает для системы в целом близкую к желаемой частотную ха­рактеристику. Согласно рис. 6.22 логарифмическая ха­рактеристика Z получит вид, представленный на рис. 6.23, что соответствует следующей передаточной функции ис­комой корректирующей обратной связи:

Это есть инерционная гибкая обратная связь с двой­ным дифференцированием (т. е. обратная связь по угло­вому ускорению исполнительного привода следящей си­стемы).

В заключение, ввиду использования здесь приближен­ных равенств, необходимо уточнить получившуюся фак­тически характеристику

оцепить ее близость к желаемой, а затем изобразить фа­зовую характеристику φ(ω) (рис. 6.22) и оценить запасы

устойчивости и качество процес­сов, которые будут иметь место фактически.

Поскольку данное построение требует соблюдения «минимально-фазовости» системы, то надо проверить также устойчивость внутреннего контура системы (рис. 6.21) с передаточной функ­цией

Амплитудная частотная харак­теристика для него имеется на рис. 6.22. Нужно только по­строить фазовую частотную характеристику φ_вн(ω) и убе­диться в соблюдении частотного критерия устойчивости. Существует развитие этого метода применительно к синтезу совместно вводимых корректирующих устройств (последовательного и параллельного). Разработаны так­же и иные варианты частотных методов синтеза.

Метод корневого годографа

О качестве процесса регулирования можно судить по расположению корней характеристического уравнения (т. е. полюсов передаточной функции замкнутой си­стемы), учитывая также еще и операторный многочлен в правой части дифференциального уравнения (т. е. нули передаточной функции замкнутой системы). Вкратце об этом шла речь выше (§ 5.3).

Корневым годографом называется совокупность тра­екторий перемещения всех корней характеристического уравнения замкнутой системы при изменении какого-ли­бо параметра этой системы (например, общего коэффи­циента усиления К разомкнутой цепи данной системы).

Пусть задана передаточная функция разомкнутой цепи системы автоматического регулирования. Запишем ее в виде

где К. — общий коэффициент усиления разомкнутой це­пи, а многочлены N(s) и L(s) имеют единичные коэф­фициенты при младших членах.

Главная передаточная функция замкнутой системы для регулируемой величины по задающему воздействию g(s), как известно, имеет вид

Характеристическое уравнение замкнутой системы за­пишется соответственно в форме

Его можно записать и иначе:

Эта форма записи характеристического уравнения замкнутой системы и используется в дальнейшем. Вы­ражение (6.26) является основным уравнением метода корневого годографа.

Обозначим корни характеристического уравнения замкнутой системы:

полюса передаточной функции разомкнутой цепи [кор­ни L(s)]:

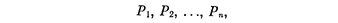
нули передаточной функции разомкнутой цепи [корпи N(s)]:

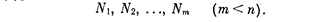
Очевидно, величины Р_i и N_q не зависят от К. Задача состоит в том, чтобы, зная расположение ну­лей N₁ , ..., N_m и полюсов P₁, ..., Р_n передаточной функ­ции разомкнутой цепи KW(s), найти корни характери­стического уравнения s₁, ..., s_m как функции параметра К. Графически это и будет корневой годограф данной системы.

Корни характеристического уравнения являются по­люсами передаточной функции замкнутой системы. Что же касается нулей этой функции, то согласно (6.25) пу­ли замкнутой системы совпадают с заданными нулями разомкнутой цепи этой системы (6.24).

Преобразуем основное уравнение метода корневого годографа. Уравнение (6.26) распадается на два: урав­нение модулей

где С — отношение коэффициентов при старших членах многочленов N(s) и L(s).

Подставим вместо s один из искомых корней харак­теристического уравнения s_k. На плоскости s = σ + jω (рис. 6.24) этот корень изобразится вектором s_k . По­строим также векторы P_i (i = 1, 2, ..., n) и N_q (q = 1, 2, ..., т) полюсов и нулей функции KW(s). Полюса Р_i будем обозна­чать крестиками, нули N_q — кружочками, а кор­ни s_k — треугольниками. На рис. 6.24 показаны также векторы величин s_k — N_q и s_k — Р_i. Обозна­чим их аргументы соот­ветственно через и , а модули: и l_i.

Тогда уравнение фаз (6.28) с учетом выражения (6.29) можно переписать в виде

а уравнение модулей (6.27) с учетом (6.29) — в виде

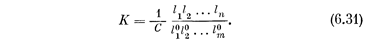
Уравнение фаз (6.30) не зависит от К. Поэтому путь решения задачи может быть такой. Сначала следует подобрать на плоскости s такое положение s_k , которое бы удовлетворяло уравнению фаз (6.30) при всех задан­ных P_i и N_q . Потом по уравнению модулей (6.31) нужно подсчитать, какой величине параметра К это соответ­ствует. Таким путем постепенно можно построить весь корневой годограф.

Рассмотрим примеры.

Пример 1. Дано

Согласно (6.29) можно написать

где

Изобразим данные нули и полюса (рис. 6.25). Заме­тим, что согласно (6.25) и (6.24) при К=0 все корни s_k совпадают с полюсами P_i Далее же легко проверить, что уравнение фаз

будет удовлетворяться для корня s₁, если он находится на оси между точками P₁ и N₁; для корня s₄ — если он лежит на оси левее точки Р₄. С увеличением К эти корни движутся как показано на рис. 6.25 стрелками.

Что же касается корней s₂ и s₃, то уравнение фаз удовлетворяется, когда они оба находятся на оси между точками P₂ и P₃ . С увеличением К они движутся навстречу друг другу. При некотором значении К они сли­ваются, а затем с увеличением К становятся комплекс­ными (сопряженными) и движутся по некоторым кривым, точки которых определяются так, чтобы удовлетво­рялось уравнение фаз. Кривые эти симметричны, по­скольку корпи сопряженные (рис. 6.25).

Величина К, отвечающая каждому конкретному положению корней, находится по уравнению модулей

Итак, траектории корней строятся только по уравне­нию фаз, а уравнение модулей используется затем для определения соответствующих значений К.

В указанном виде процесс построения будет довольно громоздким. Однако он очень упрощается при использо­вании общих свойств корневого годографа изложенных, например в [27].

Пример 2. На основе аналогичных рассуждений мо­жем построить корневой годограф для системы с пере­даточной функцией разомкнутой цепи

в виде, изображенном па рис. 6.26 при ζ > 1 и на рис. 6.27 при ζ < 1.

Проиллюстрируем на примерах некоторые элементы синтеза корректирующих устройств с помощью метода корневого годографа.

Для системы, схема которой изображена на рис. 6.28 задана передаточная функция

Требуется выбрать коэффициент усиления К и параметры последовательного корректирующего устройства

Рассмотрим два варианта: а) β = 0,1 —устройство близко к дифференцирующему; б) β=10 — устройство близко к интегрирующему.

Изобразим сначала корневой годограф системы без коррекции. В передаточной функции (6.32) имеем по­люса:

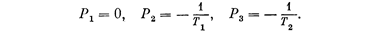
Корневой годограф показан на рис. 6.29. В случае с коррекцией (6.33) получаем

где добавляется еще один полюс и появляется один нуль:

В первом случае (β=0,1) выберем τ так, чтобы нуль N₁ расположился вблизи доминирующих корней (рис. 6.30). Полюс P₄ расположится на десятикратном расстоянии влево, т. е. будет несущественным.

Получаем новый корневой годограф (рис. 6.30). Вид­но, что «опасные» комплексные корни значительно ото­двинуты от мнимой оси, а влияние нового вещественного

корня s₁ уменьшается наличием близко расположенного нуля N₁.

Во втором случае (β = 10) новый полюс P₄ согласно (6.34) будет в десять раз ближе к началу координат, чем нуль N₁. Следовательно, Р₄ близок к нулю, а система становится близкой к дважды астатической, что увели­чивает ее точность. Корневой годограф принимает вид, изображенный на рис. 6.31.

Рассмотрим теперь включение интегро-дифференцирующего устройства с передаточной функцией

при значениях β₁ = 10, β₁ = 0,1. В этом случае имеем два добавочных полюса и два нуля:

Первый из них очень мал (почти нулевой), а второй расположен далеко влево (рис. 6.32). Корни s₁ и s₂, имев­шие неудовлетворительное расположение ранее (рис. 6.31), теперь (рис. 6.32), выходя от начала координат, влива­ются в нули N₁ и N₂. Эти корни s₁ и s₂ ближе других к мнимой оси.

Но, во-первых, они уже не могут вызвать неустойчивости и, во-вторых, их влияние нейтрализуется близко расположенными нулями. Корни же s₃ и s₄, стре­мящиеся с увеличением К вправо, располагаются доста­точно далеко от мнимой оси.

В книге [27] приведены другие примеры коррекции (неединичная обратная связь и регулирование по внеш­нему воздействию).

Другие методы синтеза рассматриваются ниже в гла­вах 7 и 8.

Список литературы

1. Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования.— М.: Наука, 1975.

2. Бесекерский В. А. Цифровые автоматические системы.— М.: Наука, 1976.

3. Болнокин В. Е., Чинаев П. И. Анализ и синтез систем автоматического управления на ЭВМ.— М.: Радио и связь,

1986.

4. Вавилов А. А., Имаев Д. X. Машинные методы расчета систем управления.—Л.: Изд-во ЛГУ, 1981.

5. Воронов А. А. Основы теории автоматического управления. Автоматическое регулирование непрерывных линейных систем.— М.: Энергия, 1980.

6. Воронов А. А. Основы теории автоматического управле­ния. Особые линейные и нелинейные системы.— М.: Энергия, 1981.

7. Воронов А. А. Устойчивость, управляемость, наблюдае­мость.— М.: Наука, 1979.

8. Динамика систем управления ракет с бортовыми вычислитель­ными машинами/Под ред. М. С. Хитрика, С. М. Федорова.— М.: Машиностроение, 1976.

9. Задачник по теории автоматического управления/Под ред. А. С. Шаталова.— М.: Энергия, 1979.

10. Иващенко Н. Н. Автоматическое регулирование.— М.: Ма­шиностроение, 1978.

11. Кочетков В. Т., Половко А. М., Пономарев В. М. Теория систем телеуправления и самонаведения ракет.— М.: Наука, 1964.

12. Красовский А. А., Поспелов Г. С. Основы автоматики и технической кибернетики.— М.: Госэнергоиздат, 1962.

13. Крутько П. Д. Обратные задачи динамики управляемых си­стем.— М.: Наука, 1987.

14. Кулешов В. С., Лакота Н. А. Динамика систем управле­ния манипуляторами.—М.: Энергия, 1971.

15. Курош А. Г. Курс высшей алгебры.— М.: Наука, 1975.

16. Макаров И. М., Менский Б. М. Линейные автоматиче­ские системы.— М.: Машиностроение, 1982.

17. Математические основы теории автоматического регулирова­ния. Т. 1, 2/Под ред. Б. К. Чемоданова.— М.: Высшая школа, 1977.

18. Мееров М. В. Исследование и оптимизация многосвязных систем управления.— М.: Наука, 1986.

19. Медведев В. С., Лесков А. Г., Ющенко А. С. Системы управления манипуляционных роботов.— М.: Наука, 1978.

20. Михаилов Ф. А. Теория и методы исследования нестацио­нарных линейных систем.— М.: Наука, 1986.

21. Морозовский В. Т. Многосвязные системы автоматическо­го регулирования.— М.: Энергия, 1970.

22. Основы автоматического регулирования и управления/Под ред. В. М. Пономарева и А. П. Литвинова.— М.: Высшая школа, 1974.

23. Основы проектирования следящих систем/Под ред. Н. А. Лакоты.— М.: Машиностроение, 1978.

24. Основы теории автоматического управления/Под ред. Н. Б. Судзиловского.— М.: Машиностроение, 1985.

25. Попов Е. П. Динамика систем автоматического регулирова­ния.— М.: Гостехиздат, 1954.

26. Попов Е. П. Автоматическое регулирование и управление.— М.: Наука, 1966.

27. Попов Е. П. Теория линейных систем автоматического ре­гулирования и управления.— М.: Наука, 1978.

28. Проектирование и расчет динамических систем/Под ред. В. А. Климова.—Л.: Машиностроение, 1974.

29. Проектирование следящих систем двустороннего действия/ Под ред. В. С. Кулешова.—М.: Машиностроение, 1979.

30. Проектирование следящих систем с помощью ЭВМ/Под ред. В. С. Медведева.— М.: Машиностроение, 1979.

31. Розенвассер Е. Н., Юсупов Р. М. Чувствительность систем управления.— М.; Наука, 1981.

32. Сборник задач по теории автоматического регулирования и уп­равления/Под ред. В. А. Бесекерского.— М.: Наука, 1978.

33. Солодов А. В., Петров Ф. С. Линейные автоматические системы с переменными параметрами.— М.: Наука, 1971.

34. Солодовников В. В., Бородин Ю. П., Иоаннисиан А. Б. Частотные методы анализа и синтеза нестационарных линейных систем.— М.: Советское радио, 1972.

35. Солодовников В. В., Плотников В. Н., Яковлев А. В. Основы теории и элементы систем автоматического регулирования.— М.: Машиностроение, 1985.

36. Теория автоматического регулирования/Под ред. В. В. Солодовникова.— Т. 1, 2.— М.: Машиностроение, 1967.

37. Теория автоматического управления/Под ред. А. В. Нетушила.— М.: Высшая школа, 1976.

38. Томович Р., Вукобратович М. Общая теория чувст­вительности.— М.: Советское радио, 1972.

39. Топчеев Ю. И., Цыпляков А. П. Задачник по теории автоматического регулирования.— М.: Машиностроение, 1977.

40. Удерман Э. Г. Метод корневого годографа в теории авто­матических систем.— М.: Наука, 1972.

41. Федоров С. М., Литвинов А. П. Автоматические систе­мы с цифровыми управляющими машинами.— М.: Энергия, 1965.

42. Фельдбаум А. А., Бутковский А. Г. Методы теории автоматического управления.— М.: Наука, 1971.

43. Цыпкин Я. 3. Основы теории автоматических систем.— М : Наука, 1977.

44. Черноруцкий Г. С., Сибрин А. П., Жабреев В. С. Следящие системы автоматических манипуляторов.— М : Наука, 1987.

45. Шаталов А. С., Барковский В. В. и др. Методы синтеза систем управления на ЦВМ.— М. Машиностроение, 1977.