Главная Случайная страница


Категории:

ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника






Порядок выполнения работы и методические указания по ее выполнению

В соответствии с индивидуальным заданием исследовать динамику и аттракторы 3х систем дифференциальных уравнений с хаотическим поведением:

1. По названию системы найти в интернете основные сведения о данной системе, области науки или технике, где данная система применяется или может быть использована для моделирования. Постараться определить какой параметр является бифуркационным и какова его область значений.

2. Для данных в задании значений параметров построить временные реализации и 3х мерный фазовый портрет.

3. Для хаотического режима показать разбегание первоначально близких траекторий. Определить время начала расхождения. Сравнить с разбеганием в другой системе.

4. Попробовать изменить значения бифуркационного параметра и найти качественно другое поведение системы, построив временные реализации и фазовый портрет. Проверить разбегание первоначально близких траекторий.

 

2.4 Контрольный пример

Рассмотрим систему дифференциальных уравнений Чуа, параметр 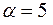, параметр является бифуркационным параметром:

1. На рис. 2.1 показаны временные реализации и фазовый портрет для значений параметров .

X(t)

Y(t)

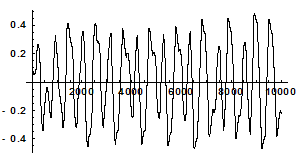Z(t)

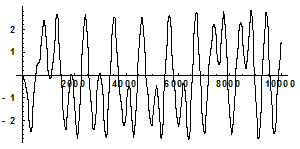
Рис. 2.1 Странный аттрактор

 

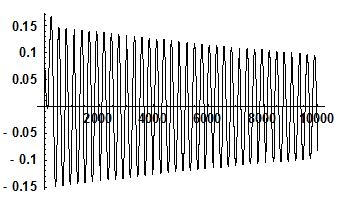
2. На рис. 2.2 показаны временные реализации и фазовый портрет для значений параметров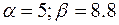

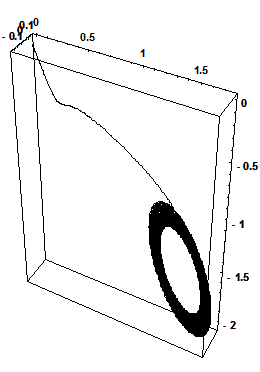X(t)

Y(t)

Z(t)

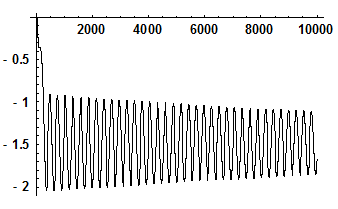
Рис. 2.5. Устойчивый фокус

 

 

3 . На рис. 2.3(а, б, в) показано разбегание первоначально близких траекторий для системы Чуа при

а) Начальные условия 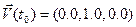б) Начальные условия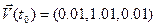

 

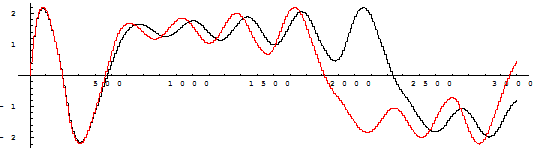
в) Расхождение начинается при

Рис. 2.3

 

2.5 Контрольные вопросы

1. Что такое временная реализация системы, фазовое пространство, фазовый портрет?

2. Что такое установившийся режим?

3. Какие бывают типы поведения системы в фазовом пространстве в установившемся режиме?

4. Что такое диссипативная система?

5. Как изменяется фазовый объем в диссипативных системах?

6. Что такое аттрактор системы?

7. Что такое аттрактор системы?

8. Что такое детерминированный хаос?

9. Какие свойства присущи системам с хаотическим поведением?

10. Как определить, является ли система хаотической?

11. Что такое показатель Ляпунова? Почему он является критерием хаоса

12. Что такое бифуркация?

13. Как построить бифуркационную диаграмму? Зачем?

14. Что такое странный аттрактор?

15. Какую геометрическую структуру имеет странный аттрактор и почему

 

2.6 Индивидуальные задания

Каждому исследовать динамику системы и построить фазовый портрет для трех систем с номерами N, N+20, N+40, где N – номер по списку в журнале.

 

         
AIZAWA circuit   dy(1) = (y(3)-b)*y(1)-d*y(2); dy(2) = d*y(1)+(y(3)-b)*y(2); dy(3)=c+a*y(3)-((y(3)^3)/3)-(y(1)^2+y(2)^2)*(1+e*y(3))+f*y(3)*y(1)^3; a=0.95; b=0.7; c = 0.6; d = 3.5; e = 0.25; f = 0.1; [0.1 0 0];
Anishchenko Astakhov circuit   if y(1)>0 I=1; else I=0; end   dy(1) = m*y(1)+y(2)-y(1)*y(3); dy(2) = -y(1); dy(3) = -g*y(3)+g*(y(1)^2)*I; m = 1.2; g = 0.5;   [0.1 0 0];  
ARNEODO circuit dy(1) = y(2); dy(2) = y(3); dy(3) = -a*y(1)-b*y(2)-y(3)+c*(y(1)^3); a = -5.5; b = 3.5; c= -1; [0.1 0 0]
Bouali circuit dy(1) = y(1)*(4-y(2))+a*y(3); dy(2) = -y(2)*(1-(y(1)^2)); dy(3) = -y(1)*(1.5-c*y(3))-0.05*y(3); a = 0.3; c= 1;   [0.1 0 0]
BrukeShaw circuit dy(1) = -c*(y(1)+y(2)); dy(2) = -y(2)-c*y(1)*y(3); dy(3) = c*y(1)*y(2)+v; v = 4.272; c= 10;   [0.1 0 0]
Cells_CNN circuit h1=0.5*(abs(y(1)+1)-abs(y(1)-1)); h2=0.5*(abs(y(2)+1)-abs(y(2)-1)); h3=0.5*(abs(y(3)+1)-abs(y(3)-1));   dy(1)=-y(1)+p1*h1-s*h2-s*h3; dy(2)=-y(2)-s*h1+p2*h2-r*h3; dy(3)=-y(3)-s*h1+r*h2+h3; p1=1.24; p2=1.1; r=4.4; s=3.21;   [0.1 0.1 0.1];
ChenCelikovsy circuit dy(1) = a*(y(2)-y(1)); dy(2) = -y(1)*y(3)+c*y(2); dy(3) = y(2)*y(1)-b*y(3); a = 36; b = 3; c = 20; [0.1 0 0];
ChenLee circuit dy(1) = a*y(1)-y(2)*y(3); dy(2) = b*y(2)+y(1)*y(3); dy(3) = c*y(3)+y(1)*y(2)*(1/3); a = 5; b = -10; c = -0.38; [0.1 0 0];
Chua's autonomous circuit nonlin=b*y(1)+0.5*(a-b)*(abs(y(1)+1)-abs(y(1)-1))   dy(1)=-alpha*y(1)+alpha*y(2)-alpha*nonlin; dy(2)=y(1)-y(2)+y(3); dy(3)=-beta*y(2); alpha=10; beta=15; a=-1.3; b=-0.7;   [1 0.2 0];
ChuaCubic circuit dx= alpha * (y - x*x*x-c*x); dy= x - y + z; dz= -beta * y; alpha=10.0; beta=16.0; c=-0.143; [0.1 0.1 0.1];  
Coullet circuit dy(1) = y(2); dy(2) = y(3); dy(3) = a*y(1)+b*y(2)+c*y(3)+d*y(1)^3; a = 0.8; b = -1.1; c = -0.45; d = -1; [0.1 0 0];
Dardras circuit dy(1) = y(2)-p*y(1)+b*y(2)*y(3); dy(2) = r*y(2)-y(1)*y(3)+y(3); dy(3) = c*y(1)*y(2)-e*y(3); p = 3; b = 2.7; r = 1.7; c = 2; e = 9; [0.1 0 0];
DequanLi circuit dy(1) = a*(y(2)-y(1))+be*y(1)*y(3); dy(2) = p*y(1)+c*y(2)-y(1)*y(3); dy(3) = b*y(3)+y(1)*y(2)-e*(y(1)^2); a = 40; be = 0.16; b=1.833; c = 20; e = 0.65; p=55;   [0.1 0 0];
Elhadj Sprott circuit dx=a*(y-x); dy=-a*x-b*y*z; dz=-c+y*y; a=40.0; b=33.0; c=10.; [0.1 0.2 0.1];
Finance circuit dy(1) = ((1/b)-a)*y(1)+y(3)+y(1)*y(2); dy(2) = -b*y(2)-y(1)^2; dy(3) = -y(1)-c*y(3); a = 0.001; b = 0.2; c = 1.1; [0.1 0 0];
Four Wing circuit   dy(1) = a*y(1)-b*y(2)*y(3); dy(2) = -c*y(2)+y(1)*y(3); dy(3) = k*y(1)-be*y(3)+y(1)*y(2); a = 4; b = 6; be = 5; c = 10; k = 1; [0.1 0 0];
FourWing2 circuit   dx=a*x+b*y+c*y*z; dy=d*y-x*z; dz=e*z+f*x*y;     a=-14.0; b=5.0; c=1.0; d=16.0; e=-43.0; f=1.0; [4 1 1];
FourWing3 circuit   dx=x+y+y*z; dy=y*z-x*z; dz=-z-a*x*y+1; a=1.0;   [1 -2 1];
GenesioTesi circuit dy(1) = y(2); dy(2) =y(3); dy(3) = -b*y(1)-be*y(2)-a*y(3)+y(1)^2; a = 0.44; b = 1; be = 1.1; [0.1 0 0];
Hadley circuit dy(1) = -y(2)^2-y(3)^2-a*y(1)+a*c; dy(2) =y(1)*y(2)-b*y(1)*y(3)-y(2)+be; dy(3) = b*y(1)*y(2)+y(1)*y(3)-y(3); a = 0.2; b = 4; be = 1; c=8; [0.1 0 0];
Halvorsen circuit dy(1)=-a*y(1)-4*y(2)-4*y(3)-y(2)*y(2); dy(2)=-a*y(2)-4*y(3)-4*y(1)-y(3)*y(3); dy(3)=-a*y(3)-4*y(1)-4*y(2)-y(1)*y(1); a=1.4;   [0.1 0 0];
Hindmarsh Rose circuit dx = (-u*x+y-a*x^3+b*x^2+z)/u; dy = -a*x^3-(d-b)*x^2+z; dz = (-s*x-z+c)/v; a = 0.49; b = 1; c = 0.0322; d = 1; s = 1; u = 0.03; v = 0.80; [0.1 0.1 0.1];  
Liu Chen circuit dy(1)=a*y(2)+b*y(1)+c*y(2)*y(3); dy(2)=d*y(2)-y(3)+e*y(1)*y(3); dy(3)=f*y(3)+g*y(1)*y(2); a=2.4; b=-3.78; c=14.0; d=-11.0; e=4.0; f=5.58; g=-1.0; [0.1 0 0];
Liu Chen1 circuit dy(1)=-a*b*y(1)/(a+b)-y(2)*y(3)+c; dy(2)=a*y(2)+y(1)*y(3); dy(3)=b*y(3)+y(1)*y(2); a=-10.0; b=-4.0; c=18.1; [0.1 0 0];
Muthuswamy Chua circuit dx=y; dy=-x/3+y/2-(y*z^2)/2; dz=y-a*z-y*z; a=0.6;   [0.1 0.1 0.1];
Newton Leipnik dy(1)=-a*y(1)+y(2)+10*y(2)*y(3); dy(2)=-y(1)-0.4*y(2)+5*y(1)*y(3); dy(3)=b*y(3)-5*y(1)*y(2); a=0.4; b=0.175;   x0=0.349; y0=0.0; z0=-0.160
Nose Hoover dy(1)=y(2); dy(2)=-y(1)+y(2)*y(3); dy(3)=a-(y(2)*y(2)); a=1.5;   [0.1 0 0];
Qi3D dx=a*(y-x)+e*y*z; dy=c*x+d*y-x*z; dz=x*y-b*z; a=16.0; b=43.0; c=-16.0; d=16.0; e=1.0; [3.0 -4.0 3.0];
QiChen dy(1)=a*(y(2)-y(1))+y(2)*y(3); dy(2)=c*y(1)-y(2)-y(1)*y(3); dy(3)=y(1)*y(2)-b*y(3); a=38.0; b=2.666; c=80.0; x0=3.0; y0=-4.0; z0=3.0;
RC_Colpitts if y(3)-y(2)<=1, nonlin=y(3)-y(2); else nonlin=1;   end dy(1)=k*k1*(y(1)-y(3))-y(1); dy(2)=2*k2*nonlin; dy(3)=2*k1*(y(1)-y(3))-2*k2*nonlin; k=2; k1=11; k2=0.9;   [0.1 0 0];
Robinson circuit dx=y; dy=x-2*x*x*x-a*y+b*x*x*y-v*y*z; dz=-c*z+d*x*x; a=0.71; b=1.8587; c=0.7061; d=0.1; v=1.0; [0.1 0.1 0.1]
Rucklidge dy(1)=-k*y(1)+a*y(2)-y(2)*y(3); dy(2)=y(1); dy(3)=-y(3)+y(2)*y(2); k=2.0; a=6.7;   [0.1 0 0];
ShimizuMorioka dy(1) =y(2); dy(2) =(1-y(3))*y(1)-a*y(2); dy(3) =(y(1)*y(1))-b*y(3); a=0.75; b=0.45;   [0.1 0 0];
SprottLinzA dx=y; dy=-x+y*z; dz=1-y^2;   [0.10 0.10 0.10];
SprottLinzB dx=y*z; dy=x-y; dz=1-x*y;   [1 0 1];
SprottLinzС dx=y*z; dy=x-y; dz=1-x^2;   [1 0 1];
SprottLinzD dx=-y; dy=x+z; dz=x*z+a*y^2;   [0.1 0 0];
SprottLinzЕ dx=y*z; dy=x^2-y; dz=1-a*x;   [1 0 0];
SprottLinzF dx=y+z; dy=-x+a*y; dz=x^2-z;   [0.1 0 0];
SprottLinzG dx=a*x+z; dy=x*z-y; dz=-x+y;   [1 0 0];
SprottLinzН dx=-y+z^2; dy=x+a*y; dz=x-z;   [1 0 0];
SprottLinzI dx=a*y; dy=x+z; dz=x+y^2-z;   [0.10 0.10 0.10];
SprottLinzJ dx=a*z; dy=-a*y+z; dz=-x+y+y^2;   [0.10 0.10 0.10];
SprottLinzK dx=x*y-z; dy=x-y; dz=x+a*z;   [0.1 0 0];
SprottLinzM dx=-z; dy=-x^2-y; dz=a+a*x+y; a=1.7;   [0.1 0.1 0.1];
SprottLinzN dx=-a*y; dy=x+z^2; dz=1+y-a*z; a=2.0;   [0.1 0 0];
SprottLinzO dx=y; dy=x-z; dz=x+x*z+a*y; a=2.7;   [0.1 0.1 0.1]
SprottLinzP dx=a*y+z; dy=-x+y^2; dz=x+y; a=2.7;   [0.1 0 0];
SprottLinzQ dx=-z; dy=x-y; dz=a*x+y^2+b*z; a=3.4; b=0.5;   [0.1 0.1 0.1];
SprottLinzR dx=a-y; dy=b+z; dz=x*y-z; a=0.9; b=0.4;   [0.1 0 0];
SprottLinzS dx=-x-a*y; dy=x+z^2; dz=1+x; a=4.0;   [0.1 0.1 0.1];
Strizhak Kawczynski circuit   dx=r*(y-(x-ax1)*(x-ax2)*(x-ax3)-a); dy=b-b1*z-b2*x-y; dz=q*(x-z); a=150.0; b=436.6; b1=3.714; b2=21.7; q=0.07; r=0.101115 ax1=10; ax2=11; ax3=20; [0.1 0 0];
Tamari circuit   dx=(x-a*y)*cos(z)-b*y*sin(z); dy=(x+c*y)*sin(z)+d*y*cos(z); dz=e+f*z+g*atan((1-u)*y/(1-h)*x); a=1.013; b=-0.011; c=0.02; d=0.96; e=0.0; f=0.01; g=1.0; h=0.05; u=0.05; [1 1 1];
Thomas dy(1)=-b*y(1)+sin(y(2)); dy(2)=-b*y(2)+sin(y(3)); dy(3)=-b*y(3)+sin(y(1)); b=0.19;   [0.1 0 0];
TSUCS1 dy(1)=a*(y(2)-y(1))+d*y(1)*y(3); dy(2)=f*y(2)-y(1)*y(3); dy(3)=c*y(3)+y(1)*y(2)-e*y(1)*y(1); a=40.0; c=0.833; d=0.5; e=0.65; f=20.0; x0=0.1; y0=1.0; z0=-0.1;
TSUCS2 dy(1)=a*(y(2)-y(1))+d*y(1)*y(3); dy(2)=b*y(1)-y(1)*y(3)+f*y(2); dy(3)=c*y(3)+y(1)*y(2)-e*y(1)*y(1); a=40.0; b=55.0; c=1.833; d=0.16; e=0.65; f=20.0; x0=0.1; y0=1.0; z0=-0.1;
Wang circuit   dx=a*(x-y)-y*z; dy=-b*y+x*z; dz=-c*z+d*x+x*y; a=0.977; b=10.0; c=4.0; d=0.1; [0.1 0.1 0.1];
Wang Sun circuit dy(1)=a*y(1)+c*y(2)*y(3); dy(2)=b*y(1)+d*y(2)-y(1)*y(3); dy(3)=e*y(3)+f*y(1)*y(2); a=0.2; b=-0.01; c=1.0; d=-0.4; e=-1.0; f=-1.0; x0=0.30; y0=0.10; z0=1.00;
Wimol Banlue dy(1)=y(2)-y(1); dy(2)=-y(3)*tanh(y(1)); dy(3)=-a+y(1)*y(2)+abs(y(2)); a=2.0; [0.1 0.1 0.1];
Xing Yun circuit   dx=a*(y-x)+y*z*z; dy=b*(x+y)-x*z*z; dz=-c*z+e*y+x*y*z; a=50.0; b=10.0; c=13.0; e=6.0; [3.0 3.0 0.40]
Yu Wang dy(1)=a*(y(2)-y(1)); dy(2)=b*y(1)-c*y(1)*y(3); dy(3)=exp(y(1)*y(2))-d*y(3); a=10.0; b=40.0; c=2.0; d=2.5; x0=2.20; y0=2.40; z0=28.00;
Zhou circuit dx=a*(y-x); dy=b*x-x*z; dz=x*y+c*z; a=10.0; b=16.0; c=-1.0; [3 1 15];
Zhou Chen circuit dx=a*x+b*y+y*z; dy=c*y-x*z+d*y*z; dz=e*z-x*y; a=2.97; b=0.15; c=-3.0; d=1.0; e=-8.78; [3 1 1];

 

 

12

Последнее изменение этой страницы: 2016-06-09

lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...