
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Обобщенная структурная схема системы РА
Сравнивая различные системы РА, рассмотренные в п.п. 1.2—1.6, нетрудно установить, что их структурные схемы во многом повторяют одна другую. Аналогия структурных схем систем РА позволяет составить их обобщенную структурную схему (рис. 1,20). На этой схеме приняты следующие обозначения: x(t) — входной сигнал или управляющее воздействие (угол поворота линии визирования в системе автоматического сопровождения цели РЛС, частота эталонного генератора в системе фазовой подстройки частоты и т. п.); y(t) —выходной сигнал илирегулируемый параметр (угол поворота антенны РЛС, частота перестраиваемого генератора); e(t) -сигнал рассогласования, или сигнал ошибки. Работа систем РА происходит в условиях действия различных помех

На обобщенной структурной схеме системы влияние помех учитывается введением возмущающего воздействия n(t), поступающего на вход системы. Это воздействие может состоять из нескольких составляющих, например, в системе автоматического сопровождения цели РЛС оно состоит из флуктуации отраженного от цели сигнала, воздействия, возникающего из-за перемещения центра отражения радиолокационного сигнала по поверхности цели, шумов первых каскадов электронных приборов приемника и т. п. Возмущающее воздействие g(t) поступает на объект управления системы РА, это воздействие обусловлено в основном изменением условий окружающей среды (температуры, давления, влажности и т. п.) и флуктуациями источников питания.
Известно, что одним из основных недостатков непрерывных систем РА является дрейф нуля их регулировочных (амплитудных) характеристик. В обобщенной структурной схеме системы РА влияние дрейфа нуля учитывается сигналом сдвига ξ(t), например, в системах автоматического сопровождения цели РЛС сигнал ξ(t) учитывает дрейф нуля пеленгационной характеристики. Функциональные устройства (ФУ) систем РА, указанные в обобщенной структурной схеме, включают устройства измерения сигнала ошибки, исполнительные и корректирующие устройства, предназначенные для создания необходимых динамических характеристик [например, к этой части системы относится ФНЧ в системе фазовой подстройки частоты (см. рис. 1.8)]. На рис. 1.20 ОУ – объект управления (антенна в РЛС, перестраиваемый генератор в системе фазовой подстройки частоты), F(e) – дискриминатор, который, как отмечалось, имеет нелинейную характеристику. При малых сигналах ошибки амплитудная характеристика дискриминатора может быть принята линейной:
uД = kДe (1.31)
Форма дискриминационной характеристики зависит от амплитуды сигнала ошибки, что приводит к нежелательным изменениям динамических характеристик систем РА. Для исключения такой зависимости проводится нормировка сигнала по амплитуде, что достигается путем введения АРУ или ограничителя.
Иногда в системах радиоуправления радиотехнических устройств встречаются системы, структурные схемы которых отличаются от их рассмотренной обобщенной схемы, например системы автоматического сопровождения бортовых РЛС выполняются как комплексные системы, в которых для повышения точности имеется дополнительный канал. Однако в этих случаях введенная обобщенная структурная схема РА является основной для анализа ее качественных и количественных характеристик.
Классификация систем РА
Системы РА классифицируются по различным признакам. Например, по принципу построения, как отмечалось, различают системы с управлением по отклонению и возмущению.
По виду входного сигнала системы РА делятся на:
· системы стабилизации, где входной сигнал является постоянной величиной (например, системы автоматической стабилизации частоты и напряжения);
· системы программного управления, в которых входной сигнал является известной функцией (например, система управления антенной РЛС в режиме поиска);
· следящие системы, в которых входной сигнал является случайным (например, система автоматического сопровождения цели РЛС).
В зависимости от вида уравнений, описывающих процессы в системах, различают непрерывные и дискретные, линейные и нелинейные, стационарные (с постоянными параметрами) и нестационарные (с переменными параметрами) системы РА, Одна и та же система может характеризоваться несколькими признаками, например система автоматической регулировки усиления – это нестационарная нелинейная система.
В современных радиотехнических устройствах важную группу составляют цифровые системы, в состав которых входят вычислительные машины или элементы этих машин. С точки зрения математического описания цифровые системы РА являются дискретными нелинейными.
Для улучшения качества работы систем РА в управляющем устройстве могут вырабатываться не только сигналы управления, но и изменяться алгоритмы управления и перестраиваться параметры системы (коэффициенты усиления звеньев, постоянные времени корректирующих устройств), в результате чего достигается высокое качество работы системы. Подобные системы РА называются адаптивными.
ЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Уравнение состояния системы
В настоящем разделе изучается одноконтурная аналоговая динамическая система автоматического управления. Динамической называется любая физическая система, все элементы которой, и в первую очередь объект управления, описываются с помощью обыкновенных дифференциальных уравнений.
Для математического описания динамики рассматриваемой системы используется метод пространства состояний. Вводится n-мерный вектор состояния системы
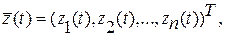 (2.1)
(2.1)
«T» - знак транспонирования.
Составляющие вектора (2.1) называются переменными состояния.
Система управляемая, поэтому вводится r-мерный вектор управления
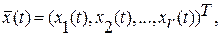 (2.2)
(2.2)
т.е. система обладает r степенями свободы и управления.
Динамика описывается системой n дифференциальных уравнений состояния, решенных относительно производных переменных состояния первого порядка
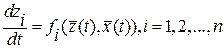 . (2.3)
. (2.3)
Векторное уравнение состояния системы имеет вид
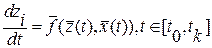 , (2.4)
, (2.4)
где  - непрерывно дифференцируемая по всем своим аргументам вектор-функция (в рассматриваемом случае стационарная).
- непрерывно дифференцируемая по всем своим аргументам вектор-функция (в рассматриваемом случае стационарная).
Переменные состояния 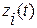 есть функции времени, в результате чего вектор состояния
есть функции времени, в результате чего вектор состояния 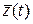 в пространстве состояния описывает кривую, называемую траекторией движения системы.
в пространстве состояния описывает кривую, называемую траекторией движения системы.
Выходные (измеряемые или наблюдаемые) величины образуют n-мерный вектор  , связанный с векторами состояния и управления зависимостью
, связанный с векторами состояния и управления зависимостью
 (2.5)
(2.5)
где 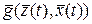 - дифференцируемая n-мерная вектор-функция.
- дифференцируемая n-мерная вектор-функция.
При заданных векторах управления 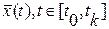 и начальных условий
и начальных условий 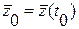 интегрирование уравнения состояния (2.4) позволяет определить зависимость
интегрирование уравнения состояния (2.4) позволяет определить зависимость  и в соответствии с уравнением (2.5) – закон изменения входной величины
и в соответствии с уравнением (2.5) – закон изменения входной величины 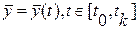 , т.е. динамический режим работы системы.
, т.е. динамический режим работы системы.
Методы линеаризации
В общем случае вектор-функции 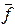 и
и 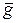 в уравнениях (2.4) и (2.5) являются нелинейными. Если эти функции удаётся линеаризовать, то изучение подобных нелинейных, но линеаризованных систем, проводятся с применением значительно более простых методов применимых для линейных систем автоматического управления.
в уравнениях (2.4) и (2.5) являются нелинейными. Если эти функции удаётся линеаризовать, то изучение подобных нелинейных, но линеаризованных систем, проводятся с применением значительно более простых методов применимых для линейных систем автоматического управления.
Методы линеаризации можно разделить на две группы:
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...