Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Показатели качества, определяемые по виду амплитудно – фазовой характеристики системы в разомкнутом состоянии (АФХ)
Как уже отмечалось, анализ системы стараются проводить на основе изучения ЛАХ. Но во всех случаях, вызывающих какие-либо сомнения необходимо использовать амплитудно-фазовую характеристику (АФХ) в разомкнутом состоянии (рис.3). В учебных целях эту характеристику необходимо использовать во всех вариантах задания.
Представляет большие трудности построение АФХ по аналитически полученным формулам. Учитывая, что для анализа системы большой точности не требуется, можно АФХ строить графически на основе имеющихся графиков ЛАХ. Действительно, ЛАХ позволяет для каждого значения частоты w графически определить значение амплитуды А(w) (L(w) = 20×lgA(w)) и фазы j(w) и, используя полярную систему координат, построить точку, принадлежащую АФХ, на комплексной плоскости. Ниже при рассмотрении конкретного примера будет продемонстрирована методика построения АФХ.
Анализ АФХ позволяет сделать следующие выводы:
а). Если системыустойчивы в разомкнутом состоянии (нулевые корни si = 0, соответствующие интегрирующим звеньям, считаются условно устойчивыми, инерционным звеньям соответствуют устойчивые корни: si = – 
),
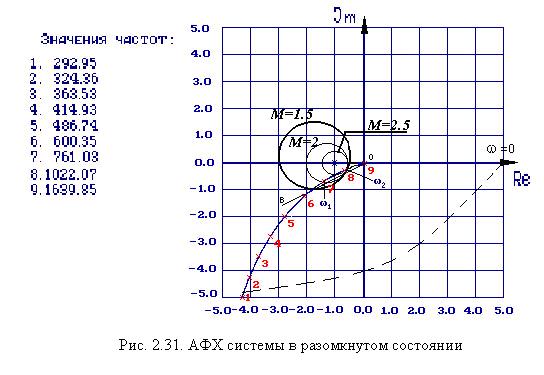
то в соответствии с критерием Найквиста замкнутая система устойчива, если АФХ не охватывает точку ( –1, 0) В случаях, когда передаточная функция системы в разомкнутом состоянии 
содержит интегрирующие звенья, АФХ дополняется дугой бесконечно большого радиуса, поворачивающую против часовой стрелки низкочастотную часть характеристики на угол, равный девяносто градусам, помноженный на число интегрирующих звеньев (рис. 2.31).
b). Характерные частоты wср и wкр и запасы устойчивости DA и Dj могут быть определены и по АФХ и, естественно, их значения должны совпадать с полученными ранее с использованием ЛАХ.
c). Колебательность системы оценивается величине показателя колебательности M.
Показатель колебательности M определяетсяпо виду амплитудно – частотной характеристики Aз(ω) (см. рис. 2.29). Задавшись некоторым значением показателя M, на графике этой характеристики проводят прямую, параллельную оси частот. Эта прямая представляет собой линию постоянного уровня показателя колебательности M нарассматриваемой характеристике.Доказывается (см. ), что геометрическое место точек, представляющее указанную линию постоянного уровня амплитудно – частотной характеристики Aз(ω) (см. рис. 2.29), переносится на комплексную плоскость с изображением АФХ.
На комплексной плоскости с изображением АФХ линии постоянного уровня показателя колебательности М представляют собой окружности с центром в точке (–С, 0).Если М>1, то С = 
, а радиус окружности R =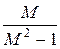 
. Концы диаметра этой окружности находятся в точках 
и 
(точки A и B на рис 2.31).
Задаваясь рядом значений М, строятокружности, из которых образуется семейство линий постоянного уровня на комплексной плоскостис изображением АФХ. Если окружность постоянного уровня пересекает график АФХ, это означает, что соответствующее ей значение М меньше максимального для рассматриваемой системы показателя колебательности. Для определения показателя колебательности требуется определить такое значение М, при котором окружность касается АФХ (окружности с меьшим значением Мцеликом находятся внутри с большим его значением).
На рис. 2.31 изображены линии постоянного уровня, которым соответствуют значения М, равные 1,5; 2; 2,5. Для рассматриваемой системы показатель колебательности М = 2.54, т.е. систему следует отнести к разряду сильно колебательных (таблица 2.4). Таким образом, построений на комплексной плоскости вполне достаточно, чтобы определить величину М, но для для большей наглядности можно построить график Аз = Аз(w).
Последнее изменение этой страницы: 2016-07-23
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...