Понятие о дискретных функциях и разностных уравнениях

Сигналы в импульсных системах могут быть представлены в виде дискретных функций времени, т. е. функций, значения которых определены только для дискретных значений аргумента t—nT. Между этими значениями независимой переменной дискретная функция равна нулю.

Дискретную функцию можно образовать из любой непрерывной функции, если принять во внимание только ее дискретные значения в равностоящие друг от друга моменты времени (рис. 3.10). Эти ординаты называют дискретами.

Дискретную функцию будем обозначать символом х (пТ), где T-период дискретности; п — любое целое число. Для того чтобы получить функцию х(пТ) по заданной непрерывной функции x(f), в последней необходимо заменить t на пТ

Рис. 3.10. Непрерывная (а) и дискретная (b) функции

Примеры непрерывных функций и соответствующих им дискретных функций приведены ниже.

Таблица 3.1

Заметим, что дискретная функция не является однозначной: ей могут соответствовать различные непрерывные или разрывные функции, если только их ординаты в моменты времени t = пТ равны значениям функции х(пТ). Для устранения этой неоднозначности в рассмотрение вводят смещенные дискретные функции, позволяющие «просматривать» процессы внутри периодов дискретности Т.

Иногда оказывается удобным перейти к относительному масштабу времени . При этом интервал между дискретами становится равным единице.

Как известно, скорость изменения непрерывной функции определяется ее первой производной. Скорость изменения дискретной функции х(мТ) характеризуется ее первой разностью, деленной на период дискретности Т. Следовательно, аналогом дифференциалов для дискретных функций являются разности, а интегралов - суммы.

Первая разность, или разность первого порядка, дискретной функции

х(пТ)Δх(пТ) = х(пТ+Т) - х(пТ) также является дискретной функцией времени.

Вторая разность, или разность второго порядка, определяется как первая разность от первой разности:

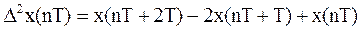или

Разность к - го порядка:

Рассмотрим пример. Дана дискретная функция х(пТ)—АпТ(рис. 3.2). Ее первая разность:

является единичной ступенчатой дискретной функцией. Вторая и высшие разности этой функции равны нулю.

Рис. 3.11. Дискретная функция (а) и ее первая разность (b)

Часто на практике вычисляют запаздывающую разность, которую легче получить техническими средствами:

Известно, что исследование динамики непрерывных систем основано на составлении и решении дифференциальных уравнений. Динамические процессы в дискретных автоматических системах описываются разностными уравнениями, или уравнениями в конечных разностях. Линейное неоднородное разностное уравнение с постоянными коэффициентами имеет следующий вид:

где х_вх(пТ) — известная дискретная функция (задающее воздействие); х_вых(пТ) -дискретная функция, определяемая уравнением (решение); Δ - разности 1-х порядков; b_i и c_i - постоянные коэффициенты.

Контрольные вопросы

1. Что такое дискретная функция времени ?

2. Что является аналогами дифференциалов и интегралов при использовании дискретных функций времени ?

3. Чем описываются динамические процессы в дискретных системах радиоавтоматики ?

3.3. Дискретное преобразование Лапласа и Z - преобразование

Удобным для решения разностных уравнений является операционный метод, основанный на дискретном преобразовании Лапласа, которое представляет собой обобщение обычного преобразования Лапласа на дискретные функции (сигналы).

Обычное прямое преобразование

где x(t) - непрерывная функция - оригинал, Х(р) - изображение.

Как известно, импульсный сигнал на выходе простейшего импульсного элемента можно представить в виде промодулированной последовательности дельта-функций:

		(3.11)

Таким образом, каждая ордината дискретной функции представляет собой δ-функцию, площадь которой определяется функцией Х(пТ). Только в этом существует формальное различие между функциями X^*(t) и Х(пТ). Но без него невозможно ввести понятия, связанные с изображениями дискретных сигналов.

Изображение сигнала x^*{t) в смысле дискретного преобразования Лапласа определяется по формуле:

		(3.12)

где X^*{t)-оригинал; Х^*(р) -изображение.

Как видно из этой формулы, дискретное преобразование устанавливает функциональную связь между дискретными функциями (сигналами) и их изображениями. Нетрудно заметить аналогию между выражениями (10) и (12). Интегралу с бесконечным пределом соответствует бесконечная сумма, непрерывному аргументу t - дискретный аргумент пТ , а непрерывной функции x(t) -дискретная функция х(пТ). По существу выражение (12) есть сумма изображений всех δ - функций, входящих в формулу (11). Под знак суммы необходимо ставить соответствующую дискретную функцию х(пТ).

Очень удобным на практике оказалось Z - преобразование, которое получается из дискретного преобразования Лапласа путем подстановки z=e ^pT:

		(3.13)

где х(пТ) - оригинал; X(z) - изображение в смысле Z- преобразования.

Рассмотрим два примера определения изображений дискретных функций.

1. Требуется определить изображение единичной ступенчатой дискретной функции х(пТ) — 1(пТ).

В соответствии с формулой (11) имеем

Z-преобразование этой функции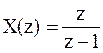

2. Дана экспоненциальная функция х(пТ)=e^anT . Найдем ее изображение :

В справочной литературе по автоматике содержатся обширные таблицы дискретного преобразования Лапласа и Z - преобразования. В таблице приведены изображения часто встречающихся функций.

Итак, изображения дискретных функций являются функциями е^pT, а не р, как это имеет место в обычном преобразовании Лапласа. В связи с этим возникла необходимость перехода к аргументу z = е^pT, который является периодической функцией частоты. Поэтому дискретные изображения и частотные спектры дискретных функций также являются периодическими функциями частоты с периодом 2π.

Таблица 3.2