Полная производная по времени от интегральной

Характеристики индивидуального объема

Рассмотрим положение объема, состоящего из одних и тех же частиц, в два последовательных момента времени t и (рис.4.2). По определению полной производной можно записать

(4.7)

где объем пространства, занимаемый рассматриваемыми частицами в момент времени .

Рис. 4.2. Положение индивидуального объема жидкости в два последующие момента времени

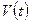Пусть объем общей части и , 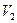—объем части пространства вновь занятого частицами подвижного объема ( часть поверхности 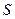, через которую частицы выходят), объем части пространства, освобожденного частицами, подвижного объема ( часть поверхности S, через которую частицы входят). Тогда каждый из интегралов по объемам 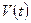и в равенстве (4.7) можно разбить на две части

,

.

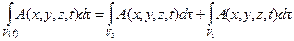Подставляя это разбиение в формулу (4.7), получаем:

. (4.8)

Первое слагаемое в правой части (4.8) равно интегралу от частной производной по времени величины :

. (4.9)

Второе и третье слагаемые можно преобразовать в интегралы по поверхности, ограничивающей подвижный объем.

(4.10)

где значения параметра в точках поверхности 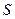. Здесь было использовано представление элементарного объема в бесконечно тонком слое вокруг поверхносте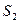й и виде объема цилиндра с площадью основания (элемент поверхности) и образующей ( проекция вектора скорости частиц на нормаль к поверхности), (рис. 4.3).

Рис. 4.3.Вычисление элементарного объема в точках

поверхности индивидуального объема

Подставляя (4.10) в (4.8) и переходя к пределу при , получаем:

. (4.11)

Здесь учтено, что для непрерывной функции имеет место равенство .

Контрольная поверхность

Физический смысл формулы (4.11) особенно ясно выявляется при использовании понятия контрольная поверхность. Контрольная поверхность - это неподвижная в пространстве поверхность, с которой в некоторый момент времени совпадает поверхность рассматриваемого подвижного объема. Поскольку контрольная поверхность и ограничиваемый ею объем части пространства неподвижны, то интеграл

представляет собой скорость изменения величины А в данном объеме пространства, а поверхностный интеграл

дает скорость изменения параметра А за счет его «потока» через контрольную поверхность.

Таким образом, полная производная по времени от некоторой интегральной характеристики подвижного объема равна частной производной по времени от этой характеристики, вычисленной для неподвижного контрольного объема, с которым подвижный объем совпадает в данный момент, плюс поток количества А через поверхность контрольного объема.

Если течение жидкости - установившееся, то во всех точках пространства

,

следовательно, для установившегося движения имеет место соотношение

. (4.12)

Это равенство означает, что при установившемся течении жидкости изменение любой интегральной характеристики подвижного объема равно потоку этой характеристики через контрольную поверхность.

Отметим, что основные теоремы механики системы материальных точек можно применять к любому подвижному объему среды, поэтому в формуле (4.10) объем и поверхность, его ограничивающая, произвольны.

Закон сохранения массы

Положим, что параметр А обозначает плотность жидкости, т.е. , тогда, согласно (4.1), имеем:

Используя формулу (4.11), получаем:

. (4.13)

Это уравнение называется уравнением неразрывности жидкости в интегральной форме.

Пусть поверхность S состоит из трех частей: , через которую жидкость втекает в контрольный объем; , через которую жидкость вытекает из контрольного объема; и 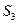- поверхности твердых тел, непроницаемой для жидкости (рис. 4.4).

Рис. 4.4.Баланс массы жидкости в канале сложной формы

Будем считать, что на поверхности единичный вектор нормали 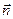направлен внутрь объема жидкости, а на поверхностях и 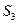- во внешность этого объема. Тогда равенство (4.13) примет вид:

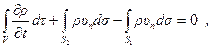
или

. (4.14)

Закон сохранения массы в форме (4.14) можно сформулировать следующим образом: масса жидкости, вошедшей в контрольную поверхность в единицу времени, минус масса жидкости, вышедшей через контрольную поверхность в единицу времени, равна изменению массы жидкости внутри контрольного объема в единицу времени.

В частности, для установившегося течения жидкости уравнение (4.14) упрощается:

.

Если жидкость течет в неподвижной трубке тока, то контрольную поверхность можно считать состоящей из трех частей: двух сечений и 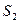, через которые жидкость соответственно втекает и вытекает в контрольную поверхность и непроницаемой боковой поверхности , на которой 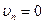(рис.4.5).

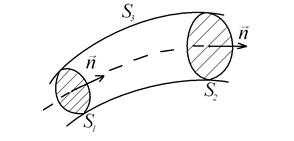
Рис. 4.5.Баланс массы жидкости в трубке тока

В этом случае общее уравнение (4.14) имеет особенно простой вид:

. (4.15)

Величину

называют массовым расходом жидкости. Формула (4.15) показывает, что массовый расход жидкости при установившемся течении постоянен вдоль трубки тока и не зависит от формы ее сечения.

Если воспользоваться определением средней по сечению скорости жидкости и понянием средней по сечению плотности жидкости, которые удволетворяют уравнению

то последнее равенство можно представить в виде

. (4.16)

Если плотность жидкости не изменяется между сечениями и , то формула (4.16) упрощается:

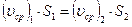. (4.17)

В частности, для таких слабосжимаемых жидкостей, какими являются вода, нефть, нефтепродукты, и которые движутся в условиях изотермического режима, предположение о неизменности плотности выполняется достаточно точно. Если же речь идет о течении этих жидкостей в трубопроводе с постоянным диаметром, 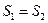, то из равенства (4.16) следует 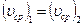, т.е. скорость таких жидкостей не изменяется по длине трубопровода.

Формула (4.17) показывает, что произведение скорости жидкости на площадь поперечного сечения трубы есть постоянная величина, поэтому там, где сечение уменьшается, средняя скорость жидкости увеличивается, и, наоборот, там, где сечение расширяется, средняя скорость жидкости уменьшается.

Формула (4.17) дает также возможность экспериментальным путем определять среднюю скорость жидкости в трубе. Если замерить объем жидкости , прошедшей через сечение трубы 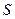за определенное время , то расход 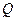и средняя скорость жидкости в этом сечении рассчитываются по формулам

. (4.18)