Дифференциальное уравнение неразрывности

Это уравнение выражает собой закон сохранения массы среды, и оно уже было получено в главе 1. Рассмотрим вывод это того уравнения, использующий интегральное представление.

В интегральной форме закон сохранения массы имеет вид (4.1)

или

.

Используя формулу Гаусса-Остроградского, можно записать

,

или

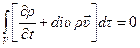
Поскольку объем 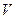произволен, то должно выполняться равенство

. (5.3)

Это уравнение называется дифференциальным уравнением неразрывности (непрерывности) потока и представляет собой первое уравнение полной системы гидродинамических уравнений. В развернутом виде оно записывается так:

. (5.4)

Таким образом, четыре функции координат и времени 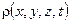, , ), удовлетворяют этому уравнению с частными производными.

Для несжимаемой жидкости плотность у каждой частицы не изменяется. Поэтому полная производная по времени от равна нулю

.

Преобразуя уравнение неразрывности (5.4), получаем:

.

Первый член в левой части этого уравнения представляет собой полную производную по времени от плотности (см. 1.8) равную нулю. Поэтому имеем

, (5.5)

т.е. для несжимаемой жидкости дивергенция вектора скорости тождественно равна нулю: .

Дифференциальные уравнения движения

Сплошной среды

Эти уравнения (уравнения движения сплошной среды в напряжениях) уже были получены в гл.1. Они выражают закон об изменении количества движения (2-й закон Ньютона). Дадим теперь вывод этих уравнений на основе общего подхода. Закон об изменении количества движения в интегральном виде записывается в виде векторного уравнения

, (5.6)

в котором сумма внешних сил определяется равенством

.

Здесь 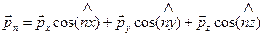- вектор напряжений в точках поверхности ; - суммарная поверхностная сила, действующая на частицы заключенные внутри поверхности со стороны счастиц среды окружающей выделенный объем 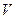; 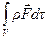- суммарная массовая сила.

Осуществляя стандартные преобразования, получаем

.

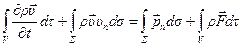Это векторное равенство можно переписать в проекциях на координатные оси

,

.

Каждое из полученных уравнений преобразуем с помощью формулы Гаусса-Остроградского. Например, первое уравнение:

,

.

Далее имеем:

.

Используя произвольность объема 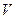, получаем

.

Аналогично имеем:

,

.

Последние три уравнения называются дифференциальными уравнениями движения сплошной среды в напряжениях. Чтобы привести их к виду (1.24), раскроем производные в левых частях уравнений и используем уравнение неразрывности (5.4). Например, для первого уравнения получаем:

Поскольку выражение в первой скобке равно нулю в силу (5.4), а выражение во второй скобке представляет собой составляющую вектора ускорения (см. 1.12), получаем первое уравнение системы:

.

Аналогичные преобразования двух оставшихся уравнений позврляют получить полную систему дифференциальных уравнений движения сплошной среды в напряжениях:

(5.8)

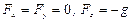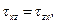
В задачах гидродинамики компоненты массовых сил обычно задаются (например, если на жидкость действует только сила тяжести, то ), а определению подлежат функции и , т.е. для определения 10 неизвестных функций имеются всего 4 уравнения (5.4), (5.8). Иными словами, система уравнений (5.4), (5.8) незамкнута.

Следует отметить, что уравнения (5.4), (5.8) справедливы для любой сплошной среды, будь то твердое тело, жидкость или газ. Поэтому, естественно, что одних только этих уравнений недостаточно, чтобы решать задачи гидромеханики. Для получения дополнительных уравнений необходимо ввести в рассмотрение конкретные свойства изучаемой среды. Математически эти свойства выражаются зависимостью между напряжениями и характеристиками деформаций, которые эти напряжения вызывают в рассматриваемой среде. Такие соотношения называются реологическими уравнениями среды. В качестве примера реологических уравнений можно назвать известный из теории упругости закон Гука, выражающий линейную связь между напряжениями и деформациями. Конкретные свойства упругого тела отражены в такой модели в виде двух коэффициентов упругости: модуля Юнга и коэффициента Пуассона.

Для вязкой жидкости реологическими уравнениями служат соотношения, выражающие линейную зависимость касательных напряжений от скоростей деформации. Эту зависимость называют законом Ньютона; в простейшем виде она встретилась нам при рассмотрении чисто сдвигового течения (глава 3). Конкретные свойства рассматриваемой жидкости отражаются в использовании в такой теории двух коэффициентов вязкости.

Существует целое направление в механике сплошных сред, которое называется реологией. Основная задача этого направления изучать связь между напряжениями и деформациями (и даже производными от этих величин) для различных классов сплошных сред.

Течение идеальной жидкости.

Уравнения Эйлера

Наиболее просто замкнутая система дифференциальных уравнений записывается в случае модели идеальной жидкости (см. гл. 3), используемой в задачах гидромеханики, в которых касательные напряжения (например, напряжения трения) намного меньше, чем нормальные (силы давления), и поэтому могут не учитываться. Для получения модели идеальной жидкости следует положить

Тогда получается система четырех уравнений

(5.9)

для пяти неизвестных функций и .

В общем случае для замыкания этой системы уравнений используется связь между плотностью жидкости и давлением. Если эта связь не содержит температуру

(5.10)

(такая жидкость называется баротропной), то получается замкнутая система пяти уравнений (5.9) - (5.10) для определения пяти функций. В частности, для однородной несжимаемой жидкости, движущейся в условиях изотермического режима, система уравнений особенно упрощается и принимает вид:

(5.10)

где

Существует большей раздел гидромеханики, посвященный решению различных задач в рамках модели идеальной жидкости. К числу таких задач относится большинство проблем газовой динамики, аэромеханики и др.

Если зависимость плотности от давления содержит температуру, то уравнений (5.9), (5.10) недостаточно для получения замкнутой системы уравнений, поскольку появляется еще одна неизвестная функция — температура. В этом случае необходимо привлекать к рассмотрению уравнение, выражающее закон сохранения энергии (4.49).