Размерно-зависимые и размерно-независимые величины

Прежде, чем перейти к доказательству основной теоремы теории размерности, введем понятия о размерно-зависимых и размерно-независимых величинах.

Говорят, что величина a размерно-зависима от величин , если размерность величины a выражается через размерности этих величин по формуле

, (6.6)

т.е. существуют такие действительные числа , ,… , что равенство (6.6) выполняется. Если же таких чисел не существует, то величина a размерно-независима от величин .

Например, время t, длина l, масса m - размерно-независимые величины. Система величин: скорость, динамическая вязкость, время — также система размерно-независимых величин. Это ясно, например, из того, что в размерность вязкости входит масса, и поэтому она не может выражаться через скорость и время. Время и скорость также не могут выражаться по размерности одна через другую, поскольку в размерность скорости входит длина. Можно привести еще много примеров систем размерно-независимых величин.

Приведем пример размерно-зависимых величин. Например, давление - это величина, размерно-зависимая от динамической вязкости, ускорения свободного падения и длины. Действительно, размерность давления можно выразить через размерности трех остальных величин – вязкости, ускорения и длины. Для этого запишем размерности всех величин через размерности основных единиц:

Будем искать такие числа , и , чтобы выполнялось равенство

.

Подставив в это равенство размерности выбранных единиц через размерности основных единиц, получим

.

Приравняв показатели степеней одинаковых размерностей в правой и левой частях последнего равенства, придем к системе трех линейных уравнений

для определения трех величин , и . Эта система имеет единственное решение: . Таким образом, находим

,

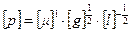что и доказывает утверждение: давление размерно-зависимо от вязкости, ускорения и длины.

Если имеется система размерных величин , то из нее всегда можно выделить подсистему, содержащую максимальное число размерно-независимых величин: , где ≤ . Делается это так. Берется величина a₁. Если она — размерная величина, то к ней добавляется величина a₂. Если a₂ имеет размерность отличную от размерности a₁ то система {a₁,a₂} состоит из размерно-независимых величин. После этого к системе величин {a₁,a₂} добавляется величина a₃. Если размерность a₃ выражается по формуле размерности через размерности величин a₁ и a₂, то берется величина a₄. Если же размерность a₃ не выражается через размерности величин a₁ и a₂, то система { } представляет собой систему размерно-независимых величин. Таким образом, перебирав все величины, входящие в систему , построим подсистему, содержащую максимальное число размерно-независимых величин.

Заметим, что если размерности всех величин выражаются через размерности L, T и M, то в такой системе имеется не более трех размерно-независимых параметров.

6.5. Доказательство основной теоремы теории размерности ( теорема Букингема)

Перейдем теперь к доказательству основной теоремы теории размерности - теоремы о том, что всякое соотношение между размерными величинами, выражающее физическую закономерность, можно записать в безразмерном (инвариантном) виде.

Пусть какая-либо физическая зависимость представляется функцией (6.5):

. (6.7)

Выделим среди размерных параметров а₁,а₂,…а_n максимальное число размерно-независимых величин. Пусть это будут величины , где ≤ . Тогда, размерности остальных параметров выражаются через размерности первых формулами

Размерность самой величины А также должна выражаться через размерности величин , поскольку если она не выражается через размерности этих величин, то она не выражается и через размерности всех величин .

Выразим размерности величин и через размерности первых аргументов , образующих подсистему размерно-независимых аргументов максимального числа

……………………………

и перепишем зависимость (6.7) в следующем виде:

где функция, получающаяся из ѓ переопределением ее аргументов.

Введем обозначения:

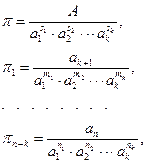(6.8)

тогда

. (6.9)

Заметим, что отношения , являющиеся аргументами функции - это безразмерные величины, поскольку размерность числителя каждой дроби совпадает с размерностью ее знаменателя (поскольку так подбирались показатели степеней , ,…, ), следовательно, их численные значения не изменяются при переходе от одной системы единиц измерения к другой.

Будем теперь произвольным образом изменять единицы измерения величин . Тогда численные значения этих величин будут также произвольно меняться. Однако параметры меняться не будут, поскольку они представляют собой безразмерные величины. Следовательно, величина не может зависеть от и соотношение (6.9) приобретает следующий окончательный вид:

. (6.10)

Таким образом, получен следующий важный результат, называемый теоремой: всякую зависимость между размерными величинами, отражающую физическую закономерность, можно записать как соотношение между безразмерными комплексами. При этом число аргументов в такой зависимости сокращается на число размерно-независимых величин, входящих в аргументы ее математической записи.

Пример: движение вязкой жидкости

В цилиндрических трубах

В качестве примера использования р-теоремы для анализа физических закономерностей рассмотрим зависимость перепада давлений при установившемся течении вязкой несжимаемой жидкости по цилиндрической трубе от гидродинамических параметров, определяющих это движение.

В качестве определяющих параметров, выберем параметры, определяющие, во-первых, свойства жидкости: плотность , вязкость 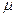; во-вторых, кинематику движения: среднюю по сечению скорость потока 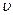; в-третьих, геометрические параметры трубы: диаметр , длину и характеристики внутренней поверхности трубы — абсолютную шероховатость Д. Под последним термином понимается среднее значение абсолютной величины выступов неровностей этой поверхности. Таким образом, изучается зависимость

. (6.11)

Определим теперь размерно-независимые параметры. Легко проверить, что таких параметров три, например, 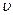, и . Действительно, скорость u и диаметр — размерно-независимые величины, потому что в одну из них входит время, а в другую время не входит. В плотность входит размерность массы, которая не участвует в определении остальных двух величин.

Функция ѓ зависит от шести размерных величин. Согласно теореме зависимость (6.11) может быть переписана в безразмерном виде, а число аргументов у функции ѓ сокращено на три, то есть останется три аргумента. Составим безразмерные комплексы, фигурирующие в формулировке теоремы. Для этого из выбранных размерно-независимых величин , и d образуем комбинации с размерностями давления, вязкости, длины. Легко проверить, что выполняются, следующие соотношения:

Тогда можно составить четыре безразмерных комплекса:

и переписать зависимость (6.11) в следующем безразмерном виде.

. (6.12)

Обозначим и . Отношение - это уже известное число Рейнольдса; параметр 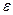называется относительной шероховатостью внутренней поверхности трубы.

Несколько изменив вид функции ѓ₁, можно записать

. (6.13)

Таким образом, отношение перепада давлений к произведению 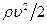зависит не от шести размерных параметров, а от трех безразмерных величин. Поэтому при постановке экспериментов по определению гидравлических потерь при движении вязкой жидкости в трубе количество необходимых опытов значительно сокращается.

Если принять во внимание, что перепад давлений с увеличением длины участка трубы l возрастает линейно, то зависимость (6.13) упрощается еще больше:

(6.14)

Обозначим

тогда

. (6.15)

Входящий в формулу (6.15) безразмерный коэффициент 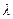называется коэффициентом гидравлического сопротивления и служит основной характеристикой гидравлических потерь при течении жидкости в трубах. Этот коэффициент будет получен при рассмотрении ламинарного течения вязкой несжимаемой жидкости в трубе (6.23). Поскольку в этом случае течение жидкости полностью рассчитывается теоретическим путем, удается найти выражение для коэффициента :

. (6.16)

Для турбулентного течения коэффициент нельзя определить расчетным путем. Поэтому его определяют либо с помощью полуэмпирических теорий турбулентности, о которых речь будет идти ниже, либо с помощью экспериментов, теорема позволяет выделить основные параметры, от которых зависит этот коэффициент.

Из уравнения Бернулли (4.8), записанного для горизонтальной трубы постоянного диаметра, следует

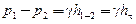. (6.17)

Сравнение формул (6.15) и (6.17) дает

. (6.18)

Формулу (6.18) называют формулой Дарси-Вейсбаха. Она служит для определения гидравлических потерь в вязкой несжимаемой жидкости, движущейся в трубе, из-за сил внутреннего вязкого трения. При этом предполагается, что коэффициент 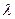как функция своих параметров определен тем или иным способом. Поэтому определение коэффициента гидравлического сопротивления при различных режимах движения жидкости является одной из важных задач гидравлики.

Часто вместо величины используется величина удельных (на единицу длины) потерь напора

, (6.19)

называемая гидравлическим уклоном. При ламинарном течении эта величина равна

. (6.20)