В турбулентном течении жидкости в круглой трубе

Потери напора на трение при течении жидкости в трубах определяются формулой (6.18) Дарси-Вейсбаха

, (8.1)

в которой безразмерный параметр 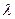называется коэффициентом гидравлического сопротивления (для течений вязкой несжимаемой жидкости в круглой трубе ).

Для ламинарного течения, которое поддается аналитическому расчету, коэффициент гидравлического сопротивления определяется формулой (7.27) (см. п.4 гл.7), а потери напора оказываются пропорциональными первой степени средней по сечению скорости :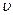

.

Для турбулентного течения характер сопротивления резко изменяется, линейная зависимость от 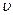нарушается. В турбулентном режиме коэффициент гидравлического сопротивления 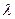зависит уже не только от числа , но и от относительной эквивалентной шероховатости 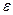внутренней поверхности трубы, т. е.

, (8.2)

где , где — средняя высота выступов шероховатости, причем зависимость эта имеет сложный характер.

Предложено большое число формул для определения коэффициента 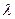в турбулентном режиме течения; это объясняется тем, что многие из предлагаемых формул получены опытным путем. Известный российский гидромеханик И.И.Никурадзе выполнил обстоятельные исследования сопротивлений гладких и шероховатых труб. Гладкость внутренней поверхности достигалась шлифовкой труб, а шероховатость — наклеиванием на гладкую поверхность калиброванных песчинок, образующих зернистую шероховатость с разным размером зерен. Естественная шероховатость поверхностей имеет, конечно, иную форму, чем наклеенные зерна песка, поэтому в гидравлике используют понятие об абсолютной эквивалентной шероховатости . Под этим термином понимают не среднюю высоту выступов шероховатости, а такую фиктивную зернистую равномерную шероховатость, при которой потери напора будут равными потерям напора в реальном трубопроводе при одинаковых расходах.

На рис. 8.3 представлены графики зависимости от числа Рейнольдса и относительной шероховатости 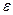, полученные Никурадзе. Если ( , см. гл.3), то течение жидкости – ламинарное; , следовательно, этот режим течения относится к течениям в области гидравлически гладких труб (зависимость от линейная).

Эксперименты показали, что при турбулентном режиме движения условно можно выделить три области чисел , в которых законы сопротивления различны.

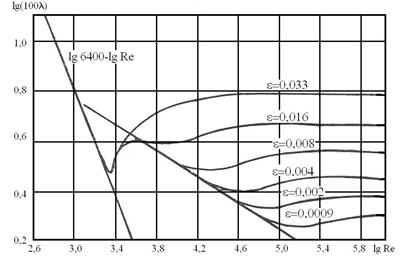
Рис. 8.3. Графики И.И. Никурадзе - зависимости

Первая область называется областью гидравлически гладких труб ( ). В этой области коэффициент 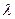зависит только от числа Re и не зависит от шероховатости 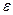внутренней поверхности трубы. В этом случае нет различия между гладкими и шероховатыми трубами, именно поэтому физически шероховатые трубы называются гидравлически гладкими.

Если , то ламинарное течение сменяется турбулентным, причем в диапазоне чисел Рейнольдса от 2320 до ( 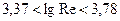) существует не полностью сформировавшееся турбулентное течение, а в диапазоне - развитое турбулентное течение.

Для расчета коэффициента 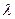гидравлического сопротивления в диапазоне чисел Рейнольдса ( ) или даже в более широком диапазоне используются формулу Блазиуса

. (8.3)

Трубы из цветных металлов, пластмассовые и стеклянные трубы могут считаться гидравлически гладкими практически во всем диапазоне чисел Re, а технические трубы - до значений , как это принято у большинства экспериментаторов. В данном диапазоне чисел Рейнольдса потеря напора пропорциональна средней скорости течения в степени 1,75:

.

В переходной области, где турбулентное течение сформировалось не полностью ( 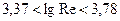) для расчета 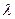можно использовать формулу Л.А.Вулиса-И.П.Гинзбурга:

, (8.4)

в которой коэффициент называют коэффициентом перемежаемости . Устройство последней формулы обеспечивает непрерывный переход от формулы (7.27) для ламинарного течения к формуле Блазиуса (8.3) для турбулентного режима течения в зоне гидравлически гладких труб.

Вторая область сопротивления труб называется областью шероховатых труб: ( ). В этой области начинает проявляться шероховатость внутренней поверхности труб и при одних и тех же числах Рейнольдса, коэффициент 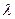имеет различные значения для труб с разной шероховатостью. В этой области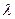 зависит как от числа Re, так и от , т.е. . Наиболее удобной формулой для вычисления 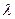является формула А.Д. Альтшуля

, (8.5)

которая при малых значениях переходит в формулу Блазиуса (8.3), а при очень больших - в формулу Б.Л. Шифринсона (см.ниже). Также можно пользоваться формулой Н.З.Френкеля

, (8.6)

Третья область сопротивления труб называют областью квадратичного трения. В этой области перестают сказываться числа Рейнольдса и все определяется лишь состоянием внутренней поверхности трубы, т.е. ее шероховатостью. В области квадратичного трения и вычисляется по формуле И.И.Никурадзе ( )

(8.7)

или по формуле Б.Л. Шифринсона

. (8.8).

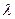Третья область называется областью квадратичного трения, потому что потеря напора в случае если не зависит от числа , пропорциональна квадрату средней скорости 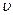течения:

.

Пример. Нефть ( , сСт) перекачивают в практически горизонтальном нефтепровод ( мм, мм, l = 100 км) с расходом м³/ч. Определить перепад давления, необходимый для перекачки.

Решение. Рассчитываем скорость 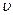течения нефти:

.

Вычисляем число Рейнольдса и относительную шероховатость:

; .

Поскольку , то режим течения нефти - турбулентный. Определяем область сопротивления, для чего вычисляем граничное число Рейнольдса:

,

следовательно, нужно использовать формулу Блазиуса.

Вычисляем коэффициент 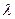по формуле (8.3) Блазиуса:

.

Для определения перепада давления используем уравнение Бернулли:

.

Учитывая, что , получаем:

,

следовательно, (Па).

Ответ: 2535198 Па или 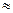2,54 МПа (25,84 ат.).

Уравнения Рейнольдса

При изучении турбулентных течений обычно вводят осредненные значения компонент скорости давления , плотности , температуры (черточки над, буквами обозначают осреднение). Тогда скорость потока в каждой точке пространства в любой момент времени можно представить в виде суммы её осреднённого значения и отклонения от него:

, (8.9)

где действительные мгновенные скорости потока в данной точке, осредненные по времени компоненты скоростей, — отклонения действительных скоростей от осредненных (пульсации скоростей).

Если осреднение параметров потока происходит по времени, то для любого осциллирующего параметра его осредненное значение находится по формуле

,

где промежуток времени, называемый периодом осреднения, достаточно велик по отношению ко времени отдельных пульсаций и мал по отношению ко времени заметного изменения средних характеристик. Если представить параметр в виде суммы , где пульсационная составляющая, то .

Воспользуемся уравнениями движения сплошной среды в напряжениях, выражающими 2-й закон Ньютона (см. гл.1). Для несжимаемой жидкости при отсутствии массовых сил эти уравнения имеют вид:

(8.10)

Учитывая уравнение неразрывности

, (8.11)

эту систему уравнений можно записать в равносильной форме:

(8.12)

Если часть членов в системе (8.12) перенести из левой части уравнений в правую, то систему можно представить в другом виде:

(8.13)

Согласно (8.9) представим каждый параметр, входящий в систему уравнений (8.13), в виде его осредненного значения и осциллирующей составляющей. Выполним осреднение уравнений (8.13) с учетом следующих свойства операции осреднения:

среднее значение пульсации равно нулю, ;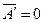

среднее значение суммы параметров равно сумме средних значений этих параметров, ;

среднее значение производной от истинной характеристики турбулентного движения равняется производной от ее среднего значения ;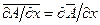

среднее значение произведения двух сомножителей, из которых только один испытывает турбулентные пульсации, равно нулю, ;

осредненное значение произведения двух пульсирующих величин равняется сумме произведения средних величин и среднего значения произведения пульсаций этих величин, .

Как результат осреднения получим систему уравнений:

(8.14)

Заметим далее, что , получим

Наконец, полученную систему уравнений можно переписать в равносильном виде, если принять во внимание осредненное уравнение неразрывности

. (8.15)

Выполнив соответствующие преобразования, придем к системе уравнений, называемых уравнениями Рейнольдса

(8.16)

Эти уравнения отличаются от уравнений движения в напряжениях (8.4) лишь тем, что к осредненным напряжениям добавились дополнительные слагаемые, представляющие собой осредненные значения произведений осциллирующих составляющих скорости течения. Эти слагаемые называют рейнольдсовскими напряжениями в честь крупнейшего английского инженера и ученого Осборна Рейнольдса (1842-1912), много сделавшего для развития теории турбулентности.

Таким образом, показано, что для осредненных параметров турбулентного течения справедливы такие же уравнения (8.10), что и для ламинарного течения, однако тензор напряжений в турбулизованной среде имеет более сложный вид:

. (8.17)