Простой трубопровод из труб разного диаметра

В рассматриваемом случае уравнение Бернулли имеет вид:

(9.18)

где — коэффициент гидравлического сопротивления для i-го участка; длина и диаметр этого участка; коэффициент k-ro местного сопротивления, имеющегося на м участке трубопровода; 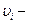скорость жидкости на м участке.

Расход Q жидкости одинаков для всех участков, а ее скорости на различных участках различны и определяются по формуле

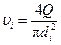. (9.19)

Подставляя из (9.19) в уравнение (9.18), получаем другую форму исходного уравнения:

(9.20)

Если заданы параметры трубопровода , , а также расход жидкости Q, то решение первой задачи практически не усложняется. Скорости жидкости на каждом участке трубопровода определяются формулой (9.19). Затем последовательно вычисляются числа Рейнольдса коэффициенты гидравлического сопротивления и коэффициенты местных сопротивлений . При этом, используются правила, изложенные в п.8.1 гл.8. Перепад напора в трубопроводе вычисляют путем непосредственной подстановки всех найденных величин в формулу (9.20).

Решение второй задачи также принципиальным образом не отличается от решения соответствующей задачи в случае, когда диаметр всего трубопровода постоянный. Третья задача, в которой требуется определить диаметры отдельных участков трубопровода по остальным параметрам перекачки, не имеет однозначного решения. Нетрудно понять, что одного уравнения недостаточно для определения нескольких неизвестных величин; для однозначного определения диаметров отдельных участков трубопровода нужны дополнительные условия. При проектировании магистральных трубопроводов для транспорта нефти, нефтепродуктов и газа такие условия диктуются соображениями надежности и экономической целесообразности.

Замечание.Во многих практически важных случаях оказывается возможным пренебречь потерями напора на местных сопротивлениях по сравнению с потерями напора на трение ( 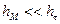). Кроме того, в ряде случаев известно заранее, что режим течения жидкости турбулентный и соответствует квадратичной области трения, т.е. . В этих случаях расчет простого трубопровода существенно упрощается. Уравнение Бернулли (9.18) принимает вид:

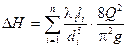. (9.21)

Если ввести коэффициент (модуль расхода):

(9.22)

то уравнение (9.21) записывается еще проще:

(9.23)

Поскольку в квадратичной области трения коэффициенты зависят только от относительной шероховатости, то коэффициенты можно вычислить заранее. Они не зависят от расхода перекачки 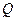, что приводит к значительному упрощению расчетов.

Уравнение (9.23) можно представить в следующем виде:

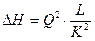, (9.24)

где длина всего трубопровода, т.е. ввести модуль расхода для всего трубопровода. Тогда этот модуль выражается формулой

. (9.25)

Иными словами, при последовательном соединении участков трубопровода с постоянным, но различным диаметром, величины складываются.

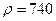
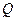Пример. Перекачку бензина ( , сСт) ведут по трубопроводу, состоящему из 3-х участков с диаметрами и длинами, равными соответственно, , , , причем расход перекачки составляет 700 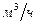. Каковы потери напора на участке трубопровода, если абсолютная шероховатость всех участков одинакова и составляет 0,15 мм? Местными сопротивлениями пренебречь.

Решение. Вычислим модуль расхода трубопровода на основании формулы (9.25), однако сначала найдем модули расхода отдельных участков.

Рассчитываем сначала скорости течения бензина на кажом из участков по формуле (9.19), а затем - числа Рейнольдса:

,

,

,

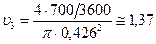
Полученные результаты показывают, что режим течения на всех участках трубопровода соответствует квадратичной области трения.

По формуле (8.8) Шифринсона вычисляем коэффициенты гидравлического сопротивления на всех участках:

, , .

По формуле (9.22) вычисляем модули расходов отдельных участков:

, , .

По формуле (9.25) вычисляем модуль расхода трубопровода:

.

По формуле (9.24) рассчитываем потери напора:

.

Ответ. 199 м.

Расчет сифона

Сифоном называется трубопровод, соединяющий два резервуара, в которых жидкость находится на разных уровнях (рис. 9.8).

Рис. 9.8. Сифонный трубопровод (сифон)

Если соединительную (сифонную) трубку заполнить жидкостью, то начнется движение жидкости из резервуара с более высоким уровнем жидкости в резервуар с более низким уровнем жидкости (рис. 9.8). Сифон относится к категории простых трубопроводов, поскольку, как правило, он не имеет ответвлений и параллельных участков. Сифоны используются для верхнего слива жидкости из железнодорожных цистерн, опорожнения водоемов, применяются при прокладке нефтепроводов через возвышенности. Сифонные трубопроводы используются при подаче воды во многих инженерных сооружениях.

Рассмотрим простейшую схему сифона, рис. 9.8. Выбирая контрольные сечения А - А и В - В, совпадающие со свободными поверхностями жидкости в каждом из резервуаров, запишем уравнение Бернулли

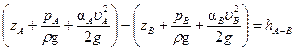. (9.26)

Это уравнение упрощается, если принять во внимание следующие обстоятельства. Давления и равны между собой и равны атмосферному давлению 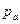. Если сифонная труба соединяет два резервуара, площади свободных поверхностей которых намного больше, чем площадь сечения трубы, то в уравнении (9.26) можно пренебречь скоростными напорами по причине их малости. Действительно, в силу уравнения неразрывности имеет место равенства расходов жидкости

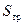где и площади свободных поверхностей жидкости в резервуарах, a площадь сечения трубопровода, следовательно, отношения скоростей жидкости обратно пропорциональны площадям поверхностей, через которые она течет. Поскольку и много больше, чем , то скорости и жидкости в резервуарах много меньше скорости 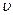жидкости в соединительном трубопроводе. Следовательно, можно принять, что основные потери напора между сечениями А - А и В - В имеют место только в сифонной трубе. С учетом этих обстоятельств уравнение Бернулли (9.26) сводится к простому уравнению

.

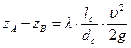или, если обозначить разность уровней жидкости в резервуарах через 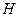, то получим уравнение

, (9.27)

где длина и диаметр сифонной трубы; расход жидкости через сифон.

Если принять, что , то тз (9.27) определится расход :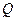

, (9.28)

из которой видно, что он пропорционален корню квадратному из разности уровней жидкости в резервуарах.

Формула (9.28) справедлива, если давление жидкости, текущей в сифоне, во всех его сечениях больше упругости насыщенных паров, в противном случае жидкость вскипит, и ее непрерывный столб в сифонном трубопроводе разорвется.

Для того чтобы сифон работал, расстояние линии гидравлического уклона до профиля трубопровода должно быть больше, чем 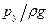. Поэтому при верхнем сливе железнодорожных цистерн отводящий трубопровод вблизи наивысшей точки делают изогутым вниз, чтобы сделать указанное расстояние максимально большим. Во всяком случае, максимальная высота 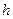трубы, над свободной поверхностью жидкости в резервуаре не должна превосходить , рис. 9.8. Эта высота тем меньше, чем выше давление насыщенных паров перекачиваемой жидкости и чем больше сопротивление в восходящей ветви сифона.