Расчет работы насосной установки.

Если жидкость может перетекать из резервуара с более высоким уровнем в резервуар с более низким уровнем сама собой, благодаря силе тяжести, то для того, чтобы подать ее из резервуара с более низким уровнем в резервуар, имеющую более высокий уровень, необходимо применение специальных устройств - насосов, затрачивающих энергию. В насосах происходит превращение потребляемой извне механической или электрической энергии в механическую энергию движения. Иными словами, внешняя энергия тратится на создание гидродинамического напора, необходимого для перекачки жидкости.

Пример насосной установки приведен на рис. 9.9. С помощью такой установки жидкость перекачивается из резервуара А в резервуар В, обладающий более высоким уровнем свободной поверхности.

Рис. 9.9. Насос для подъма жидкости из колодца

Участок трубопровода, заключенный между сечениями 1-1 и 2-2, называют линией всасывания, а участок трубопровода между сечениями 3-3 и 4-4 – линией нагнетания.

Для того чтобы жидкость двигалась от сечения 1-1 к сечению 2-2, необходимо, чтобы напор в сечении 1-1 был бльше, чем напор в сечении 2-2. Если геометрическую высоту 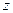отсчитывать от поверхности 1-1, на которой скорость жидкости пренебрежимо мала (считается, что площадь свободной поверхности жидкости в каждом из резервуаров намного больше площади сечения трубопровода), то напор в сечении 1-1 определяется только атмосферным давлением. Поэтому в сечении 2-2 должен существовать вакуум. Для того чтобы жидкость поступала в резервуар В необходимо, чтобы напор в сечении 3—3 выхода был больше напора в сечении 4-4.

В самом насосе жидкость движется против напора, т.е. от сечения 2-2 с меньшим напором к сечению 3-3 с большим напором. Разумеется, такое движение может осуществляться только при затрате внешней энергии.

Расчет линии всасывания

Для расчета линии всасывания, расположенной между сечениями 1-1 и 2-2, уравнение Бернулли имеет вид:

, (9.30)

где 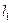, длина и диаметр линии всасывания; коэффициент ее гидравлического сопротивдления; коэффициент местного сопротивления, имеющегося в этой линии (например, всасывающие коробки , фильтра, поворотного колена, полуприкрытые заслонки и т. п.).

Полагая и пренебрегая скоростным напором в сечении 1-1 ( ), получаем:

(9.31)

Если расход 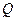жидкости задан, т.е. известна скорость течения, то уравнение (9.31) позволяет вычислить давление непосредственно перед насосом, в том числе, существующий там вакуум:

. (9.32)

Линия всасывания может работать, если , т.е. если давление в сечении 2-2 больше упругости насыщенных паров жидкости. Это должно препятствовать вскипанию жидкости из-за уменьшения давления. Проверка этого условия равносильна проверке выполнения неравенства

. (9.33)

Из (9.33) видно, что если имеет слишком большое значение, то неравенство будет нарушено, и давление в сечении 2-2 окажется меньше упругости наыщенных паров жидкости. Следовательно, если насос установлен слишком высоко над уровнем жидкости в колодце, то жидкость к такому насосу подаваться не будет. Например, для воды ( 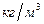, кПа) правая часть неравенства (9.29) дает:

(м).

Это означает, что насос на высоте большей, чем 10 м над уровнем воды в колодце устанавливать нельзя. На самом деле высота должна быть еще меньше, потому что в линии всасывания существует потеря напора , которая может составлять несколько метров, тем больше, чем больше расход жидкости .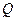

Кроме того, для нормальной работы целого ряда насосов требуется так называемый кавитационный запас . Если жидкость движется вдоль профилированной лопатки центробежного насоса, то давление в некоторых точках лопатки может уменьшиться до значения упругости насыщенных паров, в результате чего жидкость вскипит. Кавитацией (от лат. cavitas – полость) называется явление образования пузырьков, заполненных паром, при уменьшении давления в жидкости. Образовавшиеся пузырьки попадают затем в область высокого давления и там схлопываются, причем в момент схлопывания развивается огромное точечное давление, которое как удар действует на элементы проточной части насоса, разрушая их. Кавитации протеводействуют тем, что увеличивают давление на входе в насос на величину , поэтому давление на входе в насос должно быть больше . Отметим, что величина допустимого вакуума зависит также от температуры жидкости.

Расчет линии нагнетания

Для расчета линии нагнетания, расположенной между сечениями 3-3 и 4-4, уравнение Бернулли имеет вид:

, (9.34)

где , длина и диаметр линии нагнетания; коэффициент ее гидравлического сопротивления; коэффициент местного сопротивления, имеющегося в этой линии. Полагая , , , получаем

. (9.35)

Эта формула определяет величину давления в сечении 3-3 на выходе из насоса.

Если расход 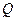жидкости задан, т.е. известна скорость течения, то уравнение (9.35) позволяет вычислить избыточное давление непосредственно после насоса:

. (9.36)

Линия нагнетания будет работать нормально, если , где максимально допустимое давление по условиям прочности трубы.

Вычислим дополнительный напор , который создает насос. Складывая почленно уравнения (9.32) и (9.36), находим

Величина создаваемого напора называется дифференциальным напором насоса. Полагая для определенности диаметры линий всасывания и нагнетания одинаковыми , получаем, что и скорости течения в них жидкости тоже одинаковые , следовательно, и имеет место следующее равенство:

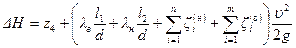. (9.37)

Таким образом, дифференциальный напор насоса равен разности высотных отметок уровней жидкости в резервуарах, сложенной с величиной суммарных потерь напора в линиях всасывания и нагнетания.

Мощность насоса

Если известны напор , который развивает насос, и расход 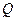жидкости, то можно установить полезную работу, которую совершает насос в единицу времени, т. е. найти его мощность. Уравнение Бернулли с учетом работы сторонних сил имеет вид

(9.38)

где суммарные потери напора за счет вязких сил внутреннего трения; мощность сторонних сил (в данном случае полезная мощность 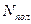насоса); весовой расход жидкости.

Применим уравнение (9.38) к рассматриваемому случаю для участка, заключенного между сечениями 1-1 и 4-4, рис. 9.9, тогда получим:

откуда находим:

.

Или

. (9.39)

Таким образом, полезная мощность насоса, затрачиваемая на перекачку жидкости, равна произведению удельного веса жидкости, ее расхода и дифференциального напора.

Учитывая, что дифференциальное давление насоса (разность давлений нагнетания и всасывания), имеем:

. (9. )

Можно также выразить полезную мощность насоса через показания вакуумметра и манометра, установленных во входном и выходном сечениях насоса, соответственно:

(9. )

Мощность, потребляемая насосом, больше полезной мощности. Отличие обусловлено целым рядом причин, приводящих к потерям в преобразовании потребляемой энергии в полезную энергию механического движения. Если ввести, коэффициент полезного действия насосной установки (которая состоит из нагнететеля и привода), то затрачиваемая на перекачку мощность связана с полезной мощностью 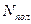формулой:

(9.40)

Расчет сложных трубопроводов

Трубопроводы называют сложными, если в них имеются точки разветвления, участки параллельного соединения, кольцевые участки, участки распределенного отбора жидкости и т. д.

Принцип расчета сложного трубопровода во многом аналогичен принципам расчета электрических цепей, обладающих той или иной геометрической конфигурацией. Поясним этот принцип на примере конкретной трубопроводной системы, изображенной на рис. 9.10.

Рис. 9.10. Сложная разветвленная трубопроводная система

Обозначим расход жидкости в трубопроводе, соединяющем между собой -ый и 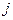-ый узел, тогда должны выполняться уравнения

узел №1: ,

узел №2: ,

узел №3: ,

узел № 4: , (9.41)

узел №5: ,

узел № 6: ,

узел № 7: ,

выражающие закон сохранения массы жидкости, проходящей через каждый узел системы. При составлении системы уравнений расходу жидкости в каждом звене был приписан определенный знак. Если в результате решения системы уравнений величина какого-либо расхода окажется отрицательной, то это означает, что жидкость в этом звене движется в направлении, противоположном выбранному.

Уравнения (9.41) образуют систему 7 линейных уравнений с 13 неизвестным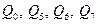и: и , потому найти однозначное решение нельзя.

Можно заметить, что расходы , , 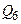и жидкости связаны уравнением

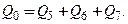
Это уравнение можно написать сразу, поскольку оно выражает очевидный факт: сколько жидкости поступает в систему, столько же жидкости отбирается из нее. Однако это уравнение можно получить из системы (9.41) путем линейной комбинации ее уравнений. Следовательно, 3 из четырех расходов , , 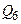и можно в известных пределах задать произвольно. Например, можно считать известным начальный расход жидкости и два расхода и в конце системы ( ), тогда расход 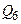определяться из условия

Таким образом, система (9.41) семи линейных уравнений содержит не 13, а 10 неизвестных величин.

Для того чтобы замкнуть систему уравнений, т.е. сделать число уравнений равным числу неизвестных, необходимо ввести в рассмотрение потери напора на отдельных участках трубопровода. Обозначим величину напора в -ом узле системы через 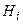и рассмотрим какой-либо замкнутый контур, например, контур 1-2-3-4-1, рис.9.10. Для этого контура можно написать:

где 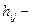потеря напора на участке , причем . Складывая почленно уравнения этой системы, получаем:

.

Таким образом, доказано, что алгебраическая сумма потерь напора на любом замкнутом контуре трубопроводной системы равна нулю.

Отметим, что понятие потеря напора используется здесь в обобщенном смысле. Если напор в начале звена больше напора в его конце, то разность напоров совпадает с величиной гидравлических потерь в этом звене, в противном случае эта разность отличается от величины гидравлических потерь знаком.

Выбрав 3 независимых контура (1-2-3-4-1), (3-2-7-6-3), (3- 6-5-4-3), получим 3 дополнительных уравнения:

(9.42)

которые совместно с системой (9.41) образуют замкнутую систему 10 алгебраических уравнений для 10 неизвестных расходов. В самом деле, каждая разность напоров определяется формулой

или (принимая во внимание, что 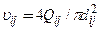) формулой

В этих формулах вместо выражения 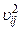. использовано выражение , которое совпадает с при условии и равно - 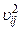в том случае, если < 0. Таким образом, предполагается, что величина может быть положительной или отрицательной в зависимости от знака скорости или, что равносильно, знака расхода .

Поскольку коэффициент гидравлического сопротивления в ом звене системы зависит от числа Рейнольдса для этого звена, т. е. определяется расходом жидкости, то станет понятно, что уравнения (9.42) представляют собой три дополнительных уравнения, но уже нелинейных, содержащих те же расходы :

Сложность расчета разветвленных трубопроводов состоит в необходимости решать систему, в общем случае, нелинейных алгебраических уравнений. Поскольку расходы жидкости в отдельных звеньях системы заранее неизвестны, то неизвестны и режимы течения жидкости в этих звеньях и, значит, заранее неизвестны формулы, которые нужно использовать для вычисления . Тем не менее, разработано множество алгоритмов решения системы уравений (9.41), (9.42) и соответствующих компьютерных программ для их численной реализации.

Существенное упрощение получается тогда, когда известно и в дальнейшем это подтверждается расчетом, что движение жидкости на всех участках системы - ламинарное. В этом случае коэффициенты гидравлического сопротивления в каждом звене обратно пропорциональны расходам жидкости, и определяются формулой

,

поэтому уравнения (9.42) становятся линейными. Разрешение системы 10-и алгебраических линейных уравнений (9.41), (9.42) с 10-ю неизвестными (или в общем случае, уравнений с неизвестными) не представляет принципиальной трудности.

Известное упрощение имеет место в другом предельном случае, часто встречающемся в практике. Если режим движения жидкости в каждом звене системы - турбулентный и сопротивление происходит в области квадратичного трения. В этом случае коэффициенты гидравлического сопротивления не зависят от чисел Рейнольдса и, значит, от расходов жидкости, поэтому уравнения (9.42) оказываются квадратными уравнениями относительно величин . Тогда задача сводится к отысканию решения системы нескольких линейных и квадратных уравнений, доступными аналитическими методами.

Что касается общего случая, то он требует рассмотрения многих вариантов, привлечения графоаналитических методов и вычислительной техники.