Сети, потоки в сетях. Теорема Форда – Фалкерсона

Эйлеровы и гамильтоновы графы

Именно с задач, поставленных и решенных в этом разделе, началась теория графов. Философ Иммануил Кант, гуляя по городу Кенигсбергу (сейчас этот город называется Калининград), поставил задачу (1736), известную в математике как задача о семи кенигсбергских мостах:можно ли пройти по всем этим мостам и при этом вернуться в исходную точку так, чтобы по каждому мосту пройти только один раз. Наш петербургский знаменитый математик швейцарского происхождения Леонард Эйлер блестяще решил эту задачу. На рис. 2 изображена схема семи мостов Кенигсберга (заметим, что сейчас осталось только два из них), а также мультиграф, соответствующий этой схеме (при построении графа считалось, что каждый берег реки и острова – это вершины графа, а мосты – его ребра; видно, что в данном случае у нас получился мультиграф без петель).

В соответствии с поставленной Кантом (и решенной Эйлером) задачей можно дать следующие определения:

Граф (или мультиграф без петель) называется эйлеровым, если существует цикл без повторения ребер (такой цикл называют эйлеровым),обходящий все вершины графа. Граф называется полуэйлеровым,если существует маршрут без повторения ребер (эйлеров путь), обходящий все ребра графа ровно один раз. На рис. 3 изображены: а – эйлеров граф, б – полуэйлеров граф и в – граф, не являющийся ни эйлеровым, ни полуэйлеровым (люди старшего поколения знают, что в школах раньше было много загадок типа “можно ли нарисовать данную фигуру не отрывая ручку от бумаги”, что и соответствует эйлерову или полуэйлерову графу).

Теорема (Эйлер). Для того чтобы данный связный граф (не орграф, но, возможно, мультиграф без петель) был эйлеровым, необходимо и достаточно, чтобы степени всех вершин были четными.Данный связный граф будет полуэйлеровым тогда и только тогда, когда степени двух вершин будут нечетными, а степени остальных вершин – четными.

Доказательство этой теоремы начнем с так называемой леммы о рукопожатиях. Название этой леммы связано с тем, что эта лемма отвечает на следующий вопрос: У Вас собрались гости. Некоторые из них здороваются друг с другом посредством рукопожатий. Какими свойствами обладает число таких людей? Ответ дается следующей достаточно простой леммой.

Лемма о рукопожатиях. Число вершин в графе (или мультиграфе без петель), имеющих нечетную степень, четно.

Заметим, что все 4 вершины мультиграфа (рис. 2), соответствующего мостам Кенигсберга, имеют степень 3. Поэтому эйлеров цикл или путь невозможен.

Примечание.Еслиграф (или мультиграф без петель) содержит 2k вершин нечетной степени, то его можно разбить на k полуэйлеровых графов (т. е. нарисовать k росчерками пера). Доказательство аналогично доказательству теоремы Эйлера.

Имеется простой алгоритм(так называемый алгоритм Флери) для нахождения эйлерова цикла (конечно, если этот цикл существует), который состоит в следующем: начинаем с любой вершины и “стираем” пройденные ребра. При этом по мосту (перешейку) проходим только, если нет других возможностей.

Очевидно, что для того чтобы построить эйлеров путьдостаточно использовать алгоритм Флери, который надо начать с вершины, имеющей нечетную степень.

Рассмотримнекоторые приложения теоремы Эйлера, которые в основном связаны с так называемой задачей китайского почтальона.

Пусть имеется некоторый граф (связный), ребрам которого приписаны некоторые числа, называемые весами ребер (часто, но не всегда!, в приложениях вес ребра – это его длина).Требуется найти такой цикл, при котором каждое ребро проходится по крайней мере один раз и суммарный вес всех ребер, вошедших в цикл, минимален. Заметим, что если граф является эйлеровым, то любой эйлеров цикл решает поставленную задачу (для эйлерова графа веса роли не играют).

Эта задача имеет много приложений, например, поливка улиц одной машиной (здесь ребра графа – дороги, а перекрестки – вершины; веса – это длины дорог), а также сбор мусора, доставка почты или даже наилучший маршрут для осмотра музея или уборка помещений и коридоров в больших учреждениях.

Заметим, что имеется алгоритм решения задачи китайского почтальона, но он требует достаточно длительного описания.

Кратко рассмотрим проблему, связанную с возможным обходом всех вершин в графе: существует ли в данном (связном) графе цикл (или маршрут), обходящий каждую вершину (кроме первой) только один раз. Если такой цикл (маршрут) существует (в этом случае такой цикл будет контуром, а маршрут – путем), то граф называется гамильтоновым (полугамильтоновым),и соответствующий цикл (путь) также называют гамильтоновым циклом (путем).

На рис. 6 изображены гамильтонов, полугамильтонов и не гамильтонов графы.

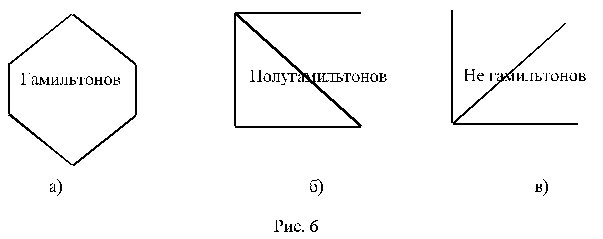
Несмотря на сходство постановки задач для гамильтоновых графов с эйлеровыми, “хорошего” решения для гамильтоновых графов нет. Вообще, о гамильтоновых графах известно очень мало. В основном – это теоремы типа “если в графе достаточное число ребер, то он гамильтонов”. Ясно, что теоремы такого типа не могут дать критерия гамильтонова графа, (рис. 6,а), поскольку в графах такого типа вершин может быть очень много, а ребер сравнительно мало).

Приведем без доказательства самую известную теорему.

Теорема(Дирак, 1952). Если в связном графе с п вершинами (при n³3) степени всех вершин больше или равны п/2, то граф гамильтонов.

Пример

Выделим компоненты связности ориентированного графа, изображенного на рис. 1. В данной задаче количество вершин n=5.

Рис. 1.

Значит, для данного ориентированного графа матрица смежности будет иметь размерность 5×5 и будет выглядеть следующим образом

.

Найдем матрицу достижимости для данного ориентированного графа по формуле 1) из утверждения:

, ,

,

Следовательно,

.

Таким образом, матрица сильной связности, будет следующей:

.

Присваиваем p=1 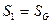и составляем множество вершин первой компоненты сильной связности G₁: это те вершины, которым соответствуют единицы в первой строке матрицы S_G. Таким образом, первая компонента сильной связности состоит из одной вершины .

Вычеркиваем из матрицы S₁ строку и столбец, соответствующие вершине v₁, чтобы получить матрицу S₂:

.

Присваиваем p=2. Множество вершин второй компоненты связности составят те вершины, которым соответствуют единицы в первой строке матрицы S₂, то есть 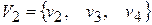. Составляем матрицу смежности для компоненты сильной связности G исходного графа G− в ее качестве возьмем подматрицу матрицы A_G, состоящую из элементов матрицы A, находящихся на пересечении строк и столбцов, соответствующих вершинам из V₂:

.

Вычеркиваем из матрицы S₂ строки и столбцы, соответствующие вершинам из V₂ ,чтобы получить матрицу S₃, которая состоит из одного элемента:

и присваиваем p=3. Таким образом, третья компонента сильной связности исходного графа, как и первая, состоит из одной вершины .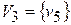

Таким образом, выделены 3 компоненты сильной связности ориентированного графа D:

G1:

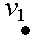
G2:

G3:

Алгоритм фронта волны.

Определение: - образ вершины - множество вершин, в которые исходят дуги из данной вершины.

Пусть необходимо найти минимальный путь из вершины в вершину .

1.Выписываются все вершины с 1 по n. Вершина помечается индексом 0.

2.Находится первый фронт волны 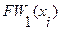как множество вершин образа вершины .

(3.17)

3.Все вершины, принадлежащие первому фронту волны, помечаются индексом 1.

4.Вводится счетчик шагов (фронтов волны) .

5.Ес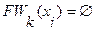ли или , то вершина недостижима из вершины, и работа алгоритма на этом заканчивается. В противном смысле переходим к пункту 6.

6. Если 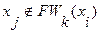, то переходим к пункту 8. В противном случае существует путь из вершины в вершину длиной в единиц, и этот путь минимальный:

7.Находятся промежуточные вершины z по правилу:

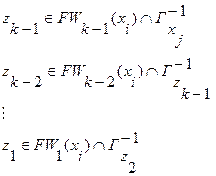, (3.18)

где - прообраз вершины - множество вершин, из которых заходят дуги в вершину

8.Определяется фронт волны как все непомеченные вершины, принадлежащие образу вершин - го фронта волны. Помечаются индексом вершины фронта волны. Далее осуществляется переход к пункту 5.

 

ПРИМЕР

Пусть задан граф матрицей смежности:

 

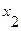
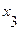
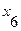
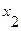
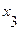
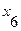
Необходимо найти минимальный путь из вершины в вершину 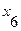(по алгоритму «фронта волны»).

1. Выпишем все вершины. Вершина помечается индексом «0»

 

2. Находится первый фронт волны:

3. Все вершины, принадлежащие первому фронту волны, помечаются индексом «1».

0 1 1

4. Так как , и , то определяем второй фронт волны:

5. Все вершины, принадлежащие второму фронту волны, помечаются индексом «2».

0 2 2 1 1

6. Так как , и , то определяем третий фронт волны:

7. Так как , то существует путь из вершины в вершину 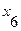длиной 3 единицы:

8. Находятся промежуточные вершины :

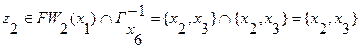
Выберем

Выберем

Таким образом, минимальный путь из вершины в вершину 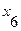имеет вид:

Пример

Найдем минимальный путь из вершины v₂ в v₆ в ориентированном нагруженном графе D, изображенном на рис. 9. В рассматриваемом графе количество вершин n=7, следовательно, матрица длин дуг ориентированного графа D будет иметь размерность 7×7.

Рис. 9.

Матрица длин дуг для рассматриваемого графа будет выглядеть следующим образом:

.

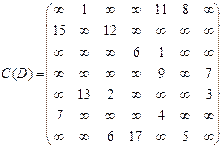Согласно алгоритму, составляем таблицу стоимости минимальных путей из вершины v₂ в вершину v_i не более, чем за k шагов, k=0,…n-1 (n=7, следовательно, k=0,…6). Как было определено выше, , и для всех остальных вершин v_i ≠ v₂, то есть первый столбец таблицы состоит из элементов, равных , кроме элемента . Второй столбец таблицы повторяет вторую строку матрицы стоимости, поскольку представляет собой стоимость возможных путей из вершины v₂ за один шаг. Далее по формуле (3.1) находим по столбцам все оставшиеся элементы таблицы. Например, чтобы найти элемент , складываем элементы столбца и первого столбца матрицы стоимости и выбираем минимальное из получившихся чисел: .

В конечном итоге получаем следующую таблицу:

Теперь необходимо по построенной таблице и по матрице C(D) восстановить минимальный путь из вершины v₂ в v₆, который будет строиться с конца, то есть, начиная с вершины v6. Для этого выбираем минимальное из чисел, стоящих в строке, соответствующей v₆ в таблице. Это число – 21 – длина минимального искомого пути. В первый раз такая длина была получена при количестве шагов, равном 4. В вершину v₆ мы можем попасть за один шаг из вершин v₁ и v₇ (длина соответствующих дуг 8 и 5 соответственно – данные из матрицы C(D)). Выбираем минимальную по длине из этих дуг. Далее, в вершину v₇ можно попасть из v₄ и v₅(длина соответствующих дуг 7 и 3 соответственно). Продолжая аналогичным образом, найдем искомый путь за 4 шага минимальной длины из вершины v₂ в v₆: v₂ v₃ v₅ v₇ v₆.

Деревья

Определение 1

Граф без циклов (ациклический граф) называется лесом.

Определение 2

Связный ациклический граф называется деревом.   Теорема 3 Для (n, m) - графа G следующие утверждения эквивалентны: 1) G-дерево; 2) G-связный граф и m= n – 1; 3) G-ациклический граф и m= n – 1; 4) любые две несовпадающие вершины графа G соединены единственной простой цепью. Доказательство   1) Þ 2) Пусть дан (n,m) граф G – связный и ациклический. Докажем индукцией по n, что m= n – 1. Базис индукции: n=1, m=0; Индуктивное предположение: допустим при n < k m=n-1; Индуктивный переход: докажем, что при n=k m=n-1. Удалив ребро, получим два дерева с числом вершин Очевидно . По индуктивному предположению Вернув ребро, получим 2) Þ 3) Пусть дан связный (n, m) граф G и m=n–1. Докажем, что G – ациклический граф. Предположим противное: в G существует цикл и пусть - ребро этого цикла. Тогда граф - связный по теореме 7 предыдущего параграфа и имеет ребра, что невозможно по теореме 9 предыдущего параграфа. Значит, граф G – ациклический. 3) Þ 4) Пусть дан ациклический (n, m)-граф G и m= n–1. Докажем, что любые две несовпадающие вершины графа G соединены единственной простой цепью. Предположим противное: пусть существуют вершины u и v, которые можно соединить по крайней мере двумя различными простыми цепями: u x1 x2 … xk v и u y1 y2 … ys v. Но тогда в графе есть цикл u x1 x2 … xk v ys… y1 y2 u, что противоречит пункту 3). Значит, любые две несовпадающие вершины графа G соединены единственной простой цепью. 4) Þ 1) Пусть любые несовпадающие вершины графа G соединены единственной простой цепью. Значит граф G – связный. Покажем, что в графе G нет циклов. Предположим противное: пусть в графе G существует цикл. Тогда любые две вершины этого цикла можно соединить по крайне мере двумя различными простыми цепями, что противоречит пункту 4). Значит, граф G – ациклический.   Теорема 4 В любом дереве порядка n³2 имеется не менее двух висячих вершин. Доказательство   Для дерева порядка n справедливо равенство (1) Допустим противное: в дереве порядка n³2 либо нет висячих вершин, либо ровно одна висячая вершина. В первом случае степень каждой вершины не меньше двух, следовательно . Во втором случае степень висячей вершины равна 1, а остальных не меньше 2, следовательно Оба неравенства противоречат равенству (1).

Определение 5

Висячая вершина дерева называется концевой вершиной. Теорема 6 Центр любого дерева состоит из одной или из двух смежных вершин. Доказательство Заметим, сперва, что концевые вершины дерева будут центральными, только если T=K1 или Т=K2. Рассмотрим дерево Т с n вершинами (n > 2) и удалим его все концевые вершины. Получим дерево, у которого центр будет тот же самый, что у дерева Т, а радиус – на единицу меньше, чем у дерева Т. Таким образом, проделав процедуру удаления всех концевых вершин некоторое число раз, мы получим или граф K1 или граф K2. Так как центр при этом не изменится, то центр произвольного дерева Т совпадет с центром графа K1 или с центром графа K2, т.е. будет состоять из двух смежных вершин, как у K2, или из одной, как у K1.

Определение 7

Простая цепь, реализующая диаметр графа, называется диаметральной цепью.

Определение 8

Граф G = (V, E) будем называть взвешенным, если существует функция f: E®R, т.е. каждому ребру графа G поставлено в соответствие некоторое вещественное число, которое называется весом (стоимостью, длиной) ребра.

Определение 9

Если остовный подграф некоторого графа является деревом, то будем называть его остовным деревом или остовом Алгоритм Краскала (алгоритм нахождения во взвешенном графе остова наибольшего или наименьшего веса).   Пусть дан связный взвешенный граф G = (V, E), çV ê= n. Цель: построение дерева Т наименьшего (наибольшего) веса являющегося остовом графа G: 0 шаг: в качестве искомого берем Т=Оn 1 шаг: выберем в G ребро наименьшего (наибольшего) веса и добавим его в Т. i шаг (к тому моменту граф Т содержит уже (i–1) ребро графа G): выбираем из оставшихся ребер графа G ребро наименьшего (наибольшего) веса, не образующий циклов с уже выбранными ребрами, и добавим его в Т. Критерий останова: алгоритм прекращает свою работу, когда уже выбрано (n–1) ребро, так как в этом случае добавление любого оставшегося ребра будет приводить к образованию цикла. Пример - остов минимального веса, – остов максимального веса.

Двудольные графы

Определение 1

Граф называется двудольным, если множество его вершин можно разбить на две части (доли) так, чтобы концы каждого ребра принадлежали разным долям.   Пример

Определение 2

Двудольный граф называется полным двудольным, если любые две его вершины, принадлежащие разным долям, смежны. Обозначают: – полный двудольный граф, где в одной доле n, а в другой доле m вершин.   Пример

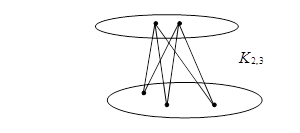
Определение 3

Граф вида называется звездой порядка n. Пример

Определение 4

Граф называется k-дольным, если множество его вершин можно разделить на k долей так, чтобы концы любого ребра принадлежали разным долям. Пример   Теорема 5 (Кёнига, критерий двудольности графа) Граф является двудольным тогда и только тогда, когда он не содержит циклов нечетной длины.   Доказательство   Необходимость. Пусть двудольный граф содержит цикл длины k. Докажем, что k – четное число. Концы всех его ребер принадлежат разным долям, поэтому, проходя по циклу, мы каждый раз попадаем из одной доли в другую. На последнем шаге мы возвращаемся в исходную вершину, а значит, делаем четное число таких «переходов», поэтому k – четное число. Достаточность. Пусть граф G не содержит циклов нечетной длины, то есть все имеющиеся в нем циклы четной длины. Разделим все вершины графа G на две части. В первую часть попадут все вершины, расстояние до которых от фиксированной вершины v четное число, и сама вершина v, а во вторую – все остальные вершины. Осталось показать, что никакие две вершины, попавшие в один класс не смежны. Предположим противное, то есть некоторые вершины x и y, принадлежащие одному из двух полученных множеств, смежны. Рассмотрим цикл, полученный в результате объединения ребра (x; y) и кратчайших цепей, соединяющих вершины x и y с вершиной v. Длина этого цикла равна сумме длин этих двух цепей плюс один. Но длины этих двух цепей одинаковой четности, поэтому их сумма – четное число, значит длина получившегося цикла – нечетное число. Пришли к противоречию, значит никакие две вершины, попавшие с один класс, не смежны.     Следствие 6   Граф является двудольным тогда и только тогда, когда он не содержит простых циклов нечетной длины.     Алгоритм поиска в ширину   Выбираем произвольную вершину в графе и приписываем ей номер ноль. Всем вершинам из ее окружения приписываем номер один. Далее рассматриваем поочередно окружение всех вершин с номером один и еще не занумерованным вершинам приписываем номер два, и так далее, пока это возможно. Если граф G связен, то поиск в ширину занумерует все его вершины. Далее разобьем множество вершин на две части , отнеся к все вершины с четными номерами, а к - все остальные. Если среди вершин множества нет смежных и среди вершин множества нет смежных (достаточно проверить все пары вершин с одинаковыми номерами), то граф G – двудольный.   Примеры Граф G не является двудольным Граф H – двудольный.   Алгоритм поиска в ширину позволяет решать следующие задачи. 1) Поиск кратчайшей цепи, соединяющей две несовпадающие вершины. 2) Разбиение множество вершин графа на области связности. 3) Поиск в ориентированном графе всех вершин, достигаемых из заданной вершины. Пример Незанумерованная вершина недостижима из вершины с номером ноль.

Эйлеровы и гамильтоновы графы

Именно с задач, поставленных и решенных в этом разделе, началась теория графов. Философ Иммануил Кант, гуляя по городу Кенигсбергу (сейчас этот город называется Калининград), поставил задачу (1736), известную в математике как задача о семи кенигсбергских мостах:можно ли пройти по всем этим мостам и при этом вернуться в исходную точку так, чтобы по каждому мосту пройти только один раз. Наш петербургский знаменитый математик швейцарского происхождения Леонард Эйлер блестяще решил эту задачу. На рис. 2 изображена схема семи мостов Кенигсберга (заметим, что сейчас осталось только два из них), а также мультиграф, соответствующий этой схеме (при построении графа считалось, что каждый берег реки и острова – это вершины графа, а мосты – его ребра; видно, что в данном случае у нас получился мультиграф без петель).

В соответствии с поставленной Кантом (и решенной Эйлером) задачей можно дать следующие определения:

Граф (или мультиграф без петель) называется эйлеровым, если существует цикл без повторения ребер (такой цикл называют эйлеровым),обходящий все вершины графа. Граф называется полуэйлеровым,если существует маршрут без повторения ребер (эйлеров путь), обходящий все ребра графа ровно один раз. На рис. 3 изображены: а – эйлеров граф, б – полуэйлеров граф и в – граф, не являющийся ни эйлеровым, ни полуэйлеровым (люди старшего поколения знают, что в школах раньше было много загадок типа “можно ли нарисовать данную фигуру не отрывая ручку от бумаги”, что и соответствует эйлерову или полуэйлерову графу).

Теорема (Эйлер). Для того чтобы данный связный граф (не орграф, но, возможно, мультиграф без петель) был эйлеровым, необходимо и достаточно, чтобы степени всех вершин были четными.Данный связный граф будет полуэйлеровым тогда и только тогда, когда степени двух вершин будут нечетными, а степени остальных вершин – четными.

Доказательство этой теоремы начнем с так называемой леммы о рукопожатиях. Название этой леммы связано с тем, что эта лемма отвечает на следующий вопрос: У Вас собрались гости. Некоторые из них здороваются друг с другом посредством рукопожатий. Какими свойствами обладает число таких людей? Ответ дается следующей достаточно простой леммой.

Лемма о рукопожатиях. Число вершин в графе (или мультиграфе без петель), имеющих нечетную степень, четно.

Заметим, что все 4 вершины мультиграфа (рис. 2), соответствующего мостам Кенигсберга, имеют степень 3. Поэтому эйлеров цикл или путь невозможен.

Примечание.Еслиграф (или мультиграф без петель) содержит 2k вершин нечетной степени, то его можно разбить на k полуэйлеровых графов (т. е. нарисовать k росчерками пера). Доказательство аналогично доказательству теоремы Эйлера.

Имеется простой алгоритм(так называемый алгоритм Флери) для нахождения эйлерова цикла (конечно, если этот цикл существует), который состоит в следующем: начинаем с любой вершины и “стираем” пройденные ребра. При этом по мосту (перешейку) проходим только, если нет других возможностей.

Очевидно, что для того чтобы построить эйлеров путьдостаточно использовать алгоритм Флери, который надо начать с вершины, имеющей нечетную степень.

Рассмотримнекоторые приложения теоремы Эйлера, которые в основном связаны с так называемой задачей китайского почтальона.

Пусть имеется некоторый граф (связный), ребрам которого приписаны некоторые числа, называемые весами ребер (часто, но не всегда!, в приложениях вес ребра – это его длина).Требуется найти такой цикл, при котором каждое ребро проходится по крайней мере один раз и суммарный вес всех ребер, вошедших в цикл, минимален. Заметим, что если граф является эйлеровым, то любой эйлеров цикл решает поставленную задачу (для эйлерова графа веса роли не играют).

Эта задача имеет много приложений, например, поливка улиц одной машиной (здесь ребра графа – дороги, а перекрестки – вершины; веса – это длины дорог), а также сбор мусора, доставка почты или даже наилучший маршрут для осмотра музея или уборка помещений и коридоров в больших учреждениях.

Заметим, что имеется алгоритм решения задачи китайского почтальона, но он требует достаточно длительного описания.

Кратко рассмотрим проблему, связанную с возможным обходом всех вершин в графе: существует ли в данном (связном) графе цикл (или маршрут), обходящий каждую вершину (кроме первой) только один раз. Если такой цикл (маршрут) существует (в этом случае такой цикл будет контуром, а маршрут – путем), то граф называется гамильтоновым (полугамильтоновым),и соответствующий цикл (путь) также называют гамильтоновым циклом (путем).

На рис. 6 изображены гамильтонов, полугамильтонов и не гамильтонов графы.

Несмотря на сходство постановки задач для гамильтоновых графов с эйлеровыми, “хорошего” решения для гамильтоновых графов нет. Вообще, о гамильтоновых графах известно очень мало. В основном – это теоремы типа “если в графе достаточное число ребер, то он гамильтонов”. Ясно, что теоремы такого типа не могут дать критерия гамильтонова графа, (рис. 6,а), поскольку в графах такого типа вершин может быть очень много, а ребер сравнительно мало).

Приведем без доказательства самую известную теорему.

Теорема(Дирак, 1952). Если в связном графе с п вершинами (при n³3) степени всех вершин больше или равны п/2, то граф гамильтонов.

Сети, потоки в сетях. Теорема Форда – Фалкерсона

Сетью называется связный граф (обычно, не орграф и не мультиграф), в котором заданы “пропускные способности” ребер, т. е. числа q_ij.Это числа большие или равные нулю, причем q_ij = 0 тогда и только тогда, когда нет ребра, соединяющего вершины i и j. Таким образом, можно считать, что пропускные способности ребер заданы для любой пары вершин. В дискретной математике пропускные способности ребер, как и все возникающие константы, считаются целыми числами (или рациональными, что одно и то же, так как рациональные числа отличаются от целых только единицами измерения). Заметим, что сети имеют огромные приложения, в частности, “сети планирования” (имеется в виду планирование производства некоторых новых, достаточно сложных изделий), где “пропускные способности” ребер – это время, за которое нужно из нескольких узлов изделия (вершин графа) получить другой (более сложный) узел. Сетевое планирование здесь не исследуется,так как гораздо больший интерес представляет сеть связи,где пропускные способности ребер – это обычно “количество одновременных разговоров”, которые могут происходить между телефонными узлами (вершинами графа).

Потоком в сети между вершиной t (источником) и s (стоком) называется набор чисел с_ij,(т. е. количество условного “груза”, перевозимого из вершины с номером i в вершину с номером j), удовлетворяющих четырем условиям:

1) числа с_ij £ 0, причем если с_ij > 0, то с_ji = 0(нет встречных перевозок);

2) числа c_ij £ q_ij (соответствующих пропускных способностей ребер);

3) если вершина с номером i – промежуточная (не совпадает с источником и стоком), то

,

т. е. количество “груза”, вывозимого из вершины i, равно количеству “груза”, ввозимого в эту вершину;

4) количество “груза”, вывозимого из источника t, должно быть равно количеству груза, ввозимого в сток s:

.

Число А называется величиной данного потока или просто потоком между t и s.

Для дальнейшего нам нужно следующее определение:

Пусть имеется некоторое сечение между вершинами t и s. Тогда величиной сечения называется сумма пропускных способностей ребер, входящих в это сечение. Сечение называется минимальным (максимальным), если его величина минимальна (максимальна).

Теорема Форда – Фалкерсона (1955). Максимальный поток между вершинами t и s равен величине минимального сечения между этими вершинами.

Доказательство этой теоремы является конструктивным (т. е. показывает, как найти нужный максимальный поток), поэтому приводится ниже.

1. Докажем сначала, что любой поток между вершинами t и s меньше или равен величине любого сечения. Пусть дан некоторый поток и некоторое сечение. Величина данного потока складывается из величин “грузов”, перевозимых по всем возможным путям из вершины t в s.Каждый такой путь обязан иметь общее ребро с данным сечением. Так как по каждому ребру сечения суммарно нельзя перевести “груза” больше, чем его пропускная способность, поэтому сумма всех грузов меньше или равна, сумме всех пропускных способностей ребер данного сечения. Утверждение доказано.

Отсюда следует, что любой поток меньше или равен величине минимального сечения, а значит и максимальный поток меньше или равен величине минимального сечения.

1. Докажем теперь обратное неравенство. Пусть имеется некоторый поток c_ij (какой-то поток всегда существует, например, нулевой,когдавсе c_ij = 0). Будем помечать вершины графа, причем считаем, что все помеченные вершины образуют множество Y.Пометки вершин производятся от источника. Каждая пометка вершины (если эта