РАСЧЕТ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

ТИПОВЫЕ ДИНАМИЧЕСКИЕ ЗВЕНЬЯ

Элементы систем автоматического регулирования могут иметь различные конструктивные формы, различные схемы и различные физические принципы действия. Однако с точки зрения теории авто­матического регулирования более целесообразно классифицировать их по динамическим свойствам. При этом для исследования процес­сов в реальных системах пользуются идеализированными схемами, которые точно описываются математически и приближенно характе­ризуют реально существующие звенья.

Как уже было сказано, динамические свойства линейных элемен­тов описываются линейными дифференциальными уравнениями. В общем случае порядок дифференциального уравнения элемента может быть произвольным. Однако такой сложный элемент всегда может быть представлен в виде сочетания так называемых типо­вых динамических звеньев, описываемых простейшими урав­нениями.

Число таких типовых динамических звеньев невелико. Они опи­сываются линейными дифференциальными уравнениями, которые имеют порядок не выше второго.

Звено называют усилительным, если его входная и выход­ная величины связаны алгебраическим уравнением вида

где К—коэффициент усиления звена.

Предполагается, что передача сигнала от входа к выходу про­изводится мгновенно, без какой-либо инерции. Поэтому усилительное звено часто называют безынерционным.

Переходная функция звена при подаче на его вход воздействия типа единичного скачка (Хвх==1) имеет вид

График переходной функции показан на рис. 12.1,а. Эта функция соответствует идеальному усилительному звену. Отклонение харак­теристики реального звена от идеального показано пунктиром.

Передаточная функция звена

Уравнение амплитудно-фазовой характеристики имеет вид

В этом выражении мнимая часть W(jω) равна нулю, а вещест­венная часть равна К.. Годограф амплитудно-фазовой характеристи­ки (рис. 12.1,6) представляет собой точку на вещественной оси на расстоянии К. от начала координат.

Примеры усилительных звеньев: рычажная и редукторная пере­дачи, манометр.

Звено называется апериодическим, если его входная и вы­ходная величины связаны дифференциальным уравнением вида

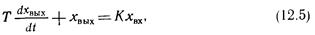
где Т и К—соответственно постоянная времени и коэффициент уси­ления звена. Такое звено также называют инерционным.

После решения уравнения (12.5) при скачкообразном характере изменения входной величины (Хвx=const) получим уравнение экспо­ненты

При t→∞ выходная величина Хвых стремится к новому установив­шемуся значению К_Хвх.

Изменяя то от 0 до ∞, подучим годограф амплитудно-фазовой характеристики звена (рис. 12.2,6). Он представляет собой полу­окружность радиусом К/2, расположенную в IV квадранте комплекс­ной плоскости с центром на вещественной оси и на расстоянии К/2 от начала координат.

Примеры апериодических звеньев: рассмотренный" сепаратор, тер­мопара, контур из сопротивления и емкости.

Звено называют интегрирующим, если его выходная величи­на пропорциональна интегралу по времени от входной величины:

Годограф амплитудно-фазовой характеристики звена показан на рис. 12.3,б. Он представляет собой прямую, совпадающую с отри­цательной мнимой полуосью координат.

Примеры интегрирующих звеньев: поршневой гидравлический ис­полнительный механизм, у которого входом является количество жидкости, подаваемой в цилиндр, а выходом — перемещение поршня; конденсатор, заряжаемый током.

Звено называется дифференцирующим, если его выходная величина пропорциональна скорости изменения входной. Различают идеальное и реальное дифференцирующее звенья.

Дифференциальное уравнение идеального дифференцирующего звена имеет вид

Так как в реальных условиях элементов, описываемых уравнения­ми типа (12.17), не существует, в число типовых звеньев вводится звено, выполняющее дифференцирующее действие более или менее приближенно. Такое звено называют реальным дифференцирующим.

Дифференциальное уравнение реального дифференцирующего звена имеет вид

После решения уравнения .(12.18) при скачкообразном характере изменения входной величины Хвx==const получим уравнение экспо­ненты

При t=0 выходная величина Хвых=К_Хвх, при t→∞ выходная вели­чина .Хвых→0. ...

Представим это выражение в виде суммы вещественной и мни­мой частей.

Годограф амплитудно-фазовой характеристики звена показан на рис. 12.4,6. Он представляет собой полуокружность радиусом К/2, расположенную в I квадранте комплексной плоскости с центром на вещественной оси и на расстоянии К/2 от начала координат.

Примеры реальных дифференцирующих звеньев: цепь с сопротив­лением и емкостью, гидравлический успокоитель с пружиной.

Звено называют колебательным, если связь между выходной и входной величинами определяется уравнением вида

Переходная функция звена при подаче на его вход единичного скачка Хвх==1(t) имеет вид

График переходной функции показан на рис. 12.5,а (кривая 1). При t→∞ эта функция стремится к новому установившемуся зна­чению, совершая вокруг него затухающие колебания с частотой ω.

Годограф амплитудно-фазовой характеристики звена показан на рис. 12.5,б. Примеры колебательных звеньев: электрический контур, содержащий емкость; индуктивность и омическое сопротивление; дифференциальный манометр.

Как уже было сказано, колебательный затухающий процесс в зве­не, описываемом уравнением (12.24), имеем лишь в том случае, когда корни характеристического уравнения являются комплексными с отрицательной вещественной частью [см. соотношение (12.28)].

Если Т -4Т >0, т.е. Т₂>2Т_1, то корни характеристического уравнения получаются вещественными. Решение уравнения (12.24) будет иметь вид

где А₁ .и А₂ постоянные интегрирования; р₁, р₂—корни характе­ристического уравнения.

Переходная функция имеет вид

График переходной функции показан на рис. 12.5,а (кривая 2). Эта функция при t→∞ стремится к новому установившемуся значению, не превышая его, т. е. апериодически.

Такое звено можно пред­ставить как два последова­тельно соединенных апериоди­ческих звена и поэтому назы­вается апериодическим звеном II порядка. Этот случай имеет большое значе­ние в практических исследова­ниях, так как такими переход­ными функциям и обладают многие технологические объ­екты.

В реальных технологиче­ских объектах часто при изме­нении входной величины выходная начинает изменяться не сразу, а по истечении некоторого времени, называемого временем запаздывания.

Для характеристики таких объектов вводится понятие звена запаздывания,: в; котором выходная величина повторяет характер изменения входной величины без искажения, но с некоторым отста­ванием по времени. Тогда объект с запаздыванием может быть представлен как сочетание рассмотренных звеньев и звена запазды­вания.

Уравнение звена запаздывания имеет вид

Годограф амплитудно-фазовой характеристики звена запаздыва­ния, построенный по уравнению (12.43), показан на рис. 12.6,6. Он представляет собой окружность с центром в начале координат и радиусом, равным единице.

Передаточная функция звена

График переходной функции звена показан на рис. 12.6,а.

СПОСОБЫ СОЕДИНЕНИЯ ЗВЕНЬЕВ

Как уже было сказано, свойства элементов и систем автоматического регулирования в динамике описываются дифференциальными уравнениями. Поэтому, если известны дифференциальные уравнения отдельных элементов, то, получив дифференциальное уравнение всей системы в целом и решение этого уравнения, можно исследовать динамические свойства системы.

Операция составления дифференциального уравнения системы может быть существенно облегчена, если реально существующие элементы системы заменить типовыми динамическими звеньями или их сочетаниями.

Схема системы автоматического регулирования, в которой реаль­но существующие элементы заменены типовыми динамическими звеньями, называется структурной схемой.

Для получения дифференциального уравнения системы необходи­мо составить ее структурную схему, найти передаточную функцию и затем от передаточной функции системы перейти к дифференци­альному уравнению.

При этом необходимо учитывать правила вычисления передаточ­ной функции соединения звеньев.

1. Система автоматического регулирования Представлена струк­турной схемой в виде трех последовательно соединенных звеньев с передаточными функциями W₁(p), W₂(p), W₃(p) (рис. 12.7,а). При таком включении выходная величина предыдущего элемента явля­ется входной величиной для последующего элемента.

Так как

3. Система автоматического регулирования состоит из двух по­следовательно соединенных звеньев, которые охвачены отрицатель­ной обратной связью (рис. 12.7,в). В практике расчета CAP линию обратной связи называют часто цепью обратной связи, а основную линию, связывающую входную и выходную величины, — прямой цепью.

Обозначим передаточную функцию элементов, расположенных в прямой цепи, через W′(p).

Тогда

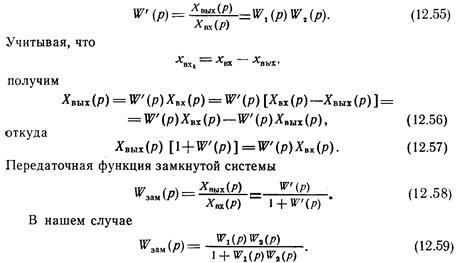
4. Система автоматического регулирования состоит из двух по­следовательно соединенных звеньев в прямой цепи, охваченных отрицательной обратной связью, в которой установлено звено с пере­даточной функцией Woc(p) (рис. 12.7,г).

Передаточная функция элементов в прямой цепи

ПОНЯТИЯ УСТОЙЧИВОСТИ СИСТЕМЫ

Как уже указывалось, основная задача системы автоматическо­го регулирования заключается в поддержании регулируемого пара­метра в пределах допуска на отклонение от заданного значения. Этому препятствует неизбежное во всякой системе наличие возму­щающих воздействий, вызывающих отклонение текущего значения регулируемого параметра от заданного. Автоматический регулятор стремится устранить это отклонение. В результате воздействия на систему возмущений и регулятора в ней возникает переходный про­цесс, который для исследуемых линейных систем описывается урав­нением вида

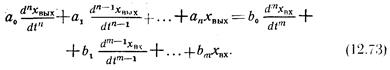
Решение этого уравнения Хвых(t)—зависимость изменения выход­ной величины (регулируемого параметра) под действием возмущения (Хвх) — может быть представлено как сумма двух составляющих:

Первая составляющая Хвых_с (t) характеризует свободное движе­ние системы и определяется свойствами системы и начальными усло­виями. Вторая составляющая Хвых_в (t) характеризует вынужден­ное движение системы и определяется свойствами системы и воз­мущающим воздействием.

Одной из основных динамических характеристик систем регули­рования является ее устойчивость. Под устойчивостью пони­мается свойство системы возвращаться к состоянию, равновесия после устранения возмущения, нарушившего указанное равновесие. Таким образом, устойчивость или неустойчивость систе­мы определяется характером ее свободного движения после снятия возмущения.

Свободное движение системы описывается однородным диф­ференциальным уравнением (без правой части):

(12,75)

Рассматривая решение этого уравнения Хвых(t) = Хвых_с (t) как отклонение регулируемого параметра от заданного значения во вре­мени, естественно потребовать, чтобы в устойчивой системе -го отклонение с течением времени стремилось к нулю:

Проанализируем возможные случаи решения уравнения (12.75) Характеристическое уравнение дифференциального уравнения (12.75) будет иметь вид:

где р₁, p₂, ..., р_n— корни этого уравнения.

Предположим, что все корни уравнения (12.77) вещественные и различные. Тогда решение дифференциального уравнения (12.75) будет иметь вид

где А_i—постоянные интегрирования, определяемые параметрами системы и начальными условиями; р_i—корни характеристического уравнения.

Если все корни р_i характеристического уравнения будут отрица­тельными, то каждая составляющая в выражении (12.78) при t, стремящемся к бесконечности, будет стремиться к нулю (рис. 12.9,а).

Если среди корней характеристического уравнения будет хотя бы один вещественный положительный корень, то соответствующая составляющая в выражении (12.78) при t, стремящемся к бесконеч­ности, будет неограниченно возрастать. Следовательно, и все выра­жение (12.78) будет стремиться к бесконечности (рис. 12.9,б).

При наличии пары комплексных корней характеристического уравнения (12.77) р_i=-σ_i+jω_i, в правую часть выражения (12.78) будет входить составляющая

где А_i—начальная амплитуда; φ_i—начальная фаза.

Если вещественная часть этих корней будет отрицательной, то при t, стремящемся к бесконечности, эта составляющая будет убы­вать по закону затухающих гармонических колебаний (рис. 12.9,в), Следовательно, и все выражение (12.78) будет стремиться к нулю.

Если вещественная часть этих корней будет положительной, то при t, стремящемся к бесконечности, эта составляющая будет воз­растать (рис. 12,9,г). Следовательно, и все выражение (12.78) будет стремиться к бесконечности.

Если среди корней характеристического уравнения (12.77) будет хотя бы одна пара комплексных корней с вещественной частью, равной нулю (мнимые корни), то в выражении (12.78) появится составляющая вида

Следовательно, переходный процесс будет иметь характер неза­тухающих колебаний (рис. 12.9,д).

Из рис. 12.9 следует, что условие (12.76) удовлетворяется только в том случае, если корни характеристического уравнения (12.77) имеют отрицательные вещественные части.

Таким образом, требование устойчивости системы автоматиче­ского регулирования сводится к условию отрицательности веще­ственных корней характеристического уравнения, а анализ системы автоматического регулирования на устойчивость—к определению знака этих корней.

КРИТЕРИИ УСТОЙЧИВОСТИ

Для определения знаков корней необходимо решить характери­стическое уравнение системы. Однако решать алгебраические урав­нения высоких порядков затруднительно. Поэтому при определении знаков корней, а следовательно, и при анализе систем на устойчи­вость используют специальные критерии, позволяющие, не при­бегая к решению характеристического уравнения, установить устой­чивость системы.

В 1895 г. швейцарский математик Гурвиц опубликовал работу, в которой изложил алгебраический критерий устойчивости, получив­ший впоследствии название критерия Гурвиц а.

Пусть характеристическое уравнение системы имеет вид:

Критерий Гурвиц а. Согласно этому критерию, все корни характеристического уравнения системы имеют отрицательные ве­щественные части (система была устойчивой) только в том случае, если определители Гурвица при а_о>0 положительны.

Главный определитель Гурвица составляется следующим обра­зом. По главной диагонали записываются все коэффициенты харак­теристического уравнения в порядке возрастания индексов, начиная с а₁. Над каждым элементом главной диагонали определителя запи­сываются коэффициенты того же характеристического уравнения в порядке возрастания индексов, а под каждым элементом — коэф­фициенты в порядке убывания индексов. На местах коэффициентов с индексами меньше 0 и больше n ставятся нули.

Главный определитель Гурвица имеет вид

В 1938 г. А. В. Михайлов предложил частотный критерий, кото­рый также исходит из характеристического уравнения замкнутой системы. Этот критерий обладает большой наглядностью в силу его простой геометрической интерпретации.

Пусть характеристическое уравнение замкнутой системы имеет вид

Будем задавать значения ω в пределах от 0 до ∞. Для каждого значения получим на комплексной плоскости вектор с координата­ ми Р(ω) и Q(ω), а соединив кон­цы этих векторов плавной кри­вой, — годограф, который- назы­вается годографом Михай­лова. По расположению этого годографа можно сделать вывод об устойчивости или неустойчи­вости системы.

Критерий Михайлова. Система регулирования устойчи­ва только в том случае, если го­дограф Михайлова F(jω) при изменении ω от 0 до ∞ проходил последовательно против часовой стрелки n квадрантов комплексной плоскости (n—степень характеристического уравнения). Виды годографов Михайлова показаны на рис. 12.11.

В 1932 г. Найквист предложил критерий, позволяющий судить об устойчивости замкнутой системы по амплитудно-фазовой характери­стике разомкнутой системы. Все системы автоматического регули­рования замкнутые. С целью исследования такой системы на устой­чивость по Найквисту ее условно размыкают и получают разомкну­тую систему.

Критерий Найквист а. Если система автоматического регу­лирования устойчива в разомкнутом состоянии, то для ее устойчиво­сти в замкнутом состоянии необходимо и достаточно, чтобы годограф амплитудно-фазовой характеристики разомкнутой системы при изменении ω от 0 до ∞ не охватывал точку на комплексной плоско­сти с координатами —1; 0 (рис. 12.13).

Разомкнутая система устойчива в том случае, если она состоит из устойчивых звеньев — апериодических, колебательных и включает не более одного интегрирующего звена.

Если разомкнутая система неустойчива, формулировка критерия более сложна (такую систему мы не приводим). В этом случае, а также при перекрестных обратных связях между звеньями систе­мы, что затрудняет ее условное размыкание, рекомендуется приме­нять другие критерии.