
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Кинематический анализ кулисно-рычажных механизмов
Графоаналитическим способом
Осуществим кинематический анализ кулисного механизма графоаналитическим способом на базе теории плоскопараллельного движения твердого тела и сложного движения точки. Предполагается, что задача о положениях звеньев механизма решена. Рассмотрим одно положение механизма, заданное углом поворота кривошипа  .
.
Исходные данные представлены в табл. 3.1, схема механизма – на рис. 3.2.
Таблица 3.1
Исходные данные механизма
| Размеры, мм |  , град , град
|  ,
град ,
град
|  ,
град ,
град
|  ,
1/c ,
1/c
|  ,
1/c2 ,
1/c2
|  ,
мм ,
мм
|  ,
мм ,
мм
| ||

| 
| 
| 176,299 | 177,961 | 31,43 | –0,763 | 198,302 | 24,24 | |
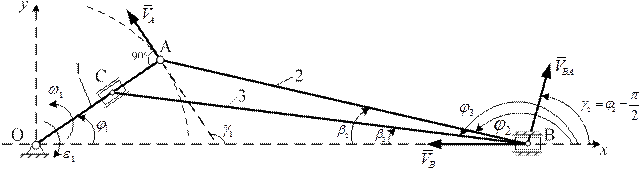
Рис. 3.2. Кинематическая схема механизма. Определение скоростей точек и угловой скорости звена АВ: 1 – кривошип; 2, 3 – шатун
Замечание. Положение кривошипа можно задать углом  .
.
1. Определение угловой скорости 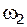 и скоростей точек звена АВ.
и скоростей точек звена АВ.
Скорость точки В согласно теореме о сложении скоростей
 , (3.5)
, (3.5)
где  , скорость точки А перпендикулярна кривошипу ОА и образует с осью Оx угол
, скорость точки А перпендикулярна кривошипу ОА и образует с осью Оx угол  .
.
Скорость  . Модуль этой скорости не может быть вычислен, так как неизвестна величина угловой скорости
. Модуль этой скорости не может быть вычислен, так как неизвестна величина угловой скорости 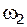 ; вектор
; вектор  направлен перпендикулярно звену АВ предположительно так, как указано на рис. 3.2, под углом
направлен перпендикулярно звену АВ предположительно так, как указано на рис. 3.2, под углом 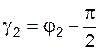 к оси Оx. Скорость точки
к оси Оx. Скорость точки  неизвестна по величине, известна линия действия вектора
неизвестна по величине, известна линия действия вектора  . Вектор
. Вектор  направлен по направляющей ОВ в сторону точки О. Истинное направление векторов
направлен по направляющей ОВ в сторону точки О. Истинное направление векторов 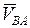 и
и  определим только после решения векторного уравнения (3.5).
определим только после решения векторного уравнения (3.5).
Для решения уравнения (3.5) выберем декартовую систему координат Оxy (рис. 3.2).
Проецируем уравнение (3.5) на эти оси координат, получаем систему уравнений скоростей:
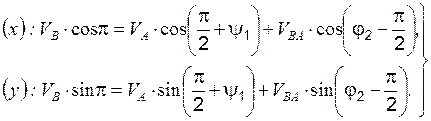 (3.6)
(3.6)
Полученную систему уравнений представляем в матричной форме 

где  ;
;  ;
;  .
.
Решение системы ,угловая скорость
,угловая скорость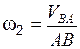 .
.
2. Определение ускорений точек и углового ускорения 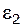 звена АВ.
звена АВ.
Согласно теореме об ускорениях точек плоской фигуры
 , (3.7)
, (3.7)
где 
Векторы 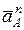 ,
,  изображены на рис. 3.3. Тогда
изображены на рис. 3.3. Тогда  .
.
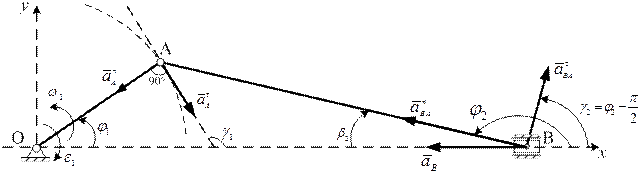
Рис. 3.3. Определение ускорений точек и углового ускорения звена АВ
Нормальное ускорение точки В во вращательном движении звена АВ вокруг полюса А  .
.
Замечание. На рис. 3.3 изображено истинное направление углового ускорения  . Его величина принимается по модулю, т. е.
. Его величина принимается по модулю, т. е. 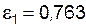 1/с2.
1/с2.
Вектор  направлен от В к А. Для векторов
направлен от В к А. Для векторов  и
и 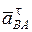 известны только линии действия этих векторов:
известны только линии действия этих векторов:  – по направляющей ОВ,
– по направляющей ОВ, 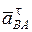 – перпендикулярно АВ. Зададимся произвольно их направлениями по указанным линиям (рис. 3.3). Эти ускорения определяются при решении векторного уравнения (3.7). Знак в ответе указывает, соответствует ли истинное направление вектора принятому при расчете.
– перпендикулярно АВ. Зададимся произвольно их направлениями по указанным линиям (рис. 3.3). Эти ускорения определяются при решении векторного уравнения (3.7). Знак в ответе указывает, соответствует ли истинное направление вектора принятому при расчете.
Проектируем уравнение (3.7) на координатные оси x и y (рис. 3.3), получаем систему уравнений «ускорений»:
 ;
;
 ;
;
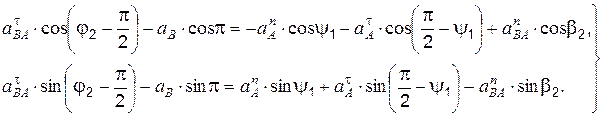 (3.8)
(3.8)
Систему уравнений (3.8) представляем в матричной форме
 ,
,
где  ;
; 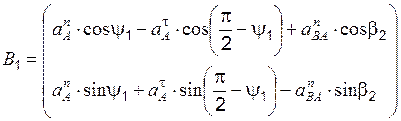 .
.
Решение системы уравнений (3.8) находим как  .
.
3. Определение угловой скорости 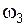 и скоростей точек звена СВ (рис. 3.4).
и скоростей точек звена СВ (рис. 3.4).

Рис. 3.4. Определение скоростей точек и угловой скорости звена СВ
Абсолютная скорость и абсолютное ускорение точки С могут быть
определены при рассмотрении плоскопараллельного движения звена ВС и сложного движения точки по звену ОА.
При решении этой задачи заданными величинами принимаются  – относительная координата ТС на кривошипе и скорость
– относительная координата ТС на кривошипе и скорость  . Подлежат определению:
. Подлежат определению:
 – угловая скорость звена СВ;
– угловая скорость звена СВ;
 – скорость ползуна С относительно кривошипа;
– скорость ползуна С относительно кривошипа;
 – угловое ускорение звена СВ;
– угловое ускорение звена СВ;
 – ускорение точки С относительно кривошипа ОА.
– ускорение точки С относительно кривошипа ОА.
Согласно теореме о скоростях точек плоской фигуры
 . (3.9)
. (3.9)
Скорость  определена ранее, ее величина и направление известны. Для вектора
определена ранее, ее величина и направление известны. Для вектора  известна только линия действия. Эта линия направлена перпендикулярно СВ. Зададимся произвольно направлением вектора
известна только линия действия. Эта линия направлена перпендикулярно СВ. Зададимся произвольно направлением вектора  по указанной линии (рис. 3.4).
по указанной линии (рис. 3.4).
Абсолютная скорость точки С неизвестна по величине и направлению.
Абсолютную скорость точки С можно определить, используя векторное уравнение (3.9).
Из уравнения следует

Модуль абсолютной скорости точки С 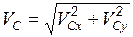 .
.
Рассмотрим сложное движение точки С.
Абсолютную скорость точки С выразим как геометрическую сумму относительной и переносной скоростей:
 .
.
Переносным движением является вращательное движение кривошипа ОА. Следовательно,  , ОС=S. Вектор
, ОС=S. Вектор  направлен перпендикулярно кривошипу ОА в сторону его вращения (рис. 3.4).
направлен перпендикулярно кривошипу ОА в сторону его вращения (рис. 3.4).
Относительное движение – движение точки С вдоль кривошипа ОА. Для относительной скорости  известна линия действия. Это прямая, совпадающая с продольной осью кривошипа. Зададимся произвольным направлением вектора по линии ОА (рис. 3.4).
известна линия действия. Это прямая, совпадающая с продольной осью кривошипа. Зададимся произвольным направлением вектора по линии ОА (рис. 3.4).
После изображения векторов скоростей укажем углы, образованные этими векторами с осями координат (рис. 3.4).
Неизвестные величины  ,
, 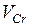 определяются при решении векторного уравнения:
определяются при решении векторного уравнения:
 . (3.10)
. (3.10)
Проецируя векторное уравнение (3.10) на оси координат Оxy
(рис. 3.4), получим
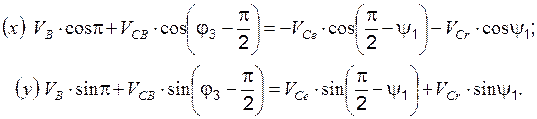
Представим эту систему уравнений в следующем виде

Матричная форма системы уравнений скоростей
 ,
,
где  ;
; 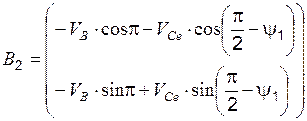 ;
;  .
.
Решение системы уравнений  .
.
4. Определение углового ускорения  и ускорений точек звена СВ.
и ускорений точек звена СВ.
Согласно теореме об ускорениях точек плоской фигуры
 . (3.11)
. (3.11)
Модуль и направление вектора  определены выше. Нормальное ускорение точки С во вращательном движении вокруг полюса В
определены выше. Нормальное ускорение точки С во вращательном движении вокруг полюса В  .
.
Вектор  направлен от С к В. Модуль вектора
направлен от С к В. Модуль вектора  неизвестен, известна только линия действия этого вектора. Она направлена перпендикулярно СВ. Зададимся произвольно направлением вектора
неизвестен, известна только линия действия этого вектора. Она направлена перпендикулярно СВ. Зададимся произвольно направлением вектора  по этой линии (рис. 3.5). Вектор направлен по направляющей ВО.
по этой линии (рис. 3.5). Вектор направлен по направляющей ВО.

Рис. 3.5. Определение ускорений точек и углового ускорения звена СВ
Абсолютное ускорение точки С равно геометрической сумме переносного, относительного и кориолисова ускорений

или
 . (3.12)
. (3.12)
Переносным движением является вращательное движение кривошипа ОА с угловой скоростью  и угловым ускорением
и угловым ускорением  .
.
Модуль переносного нормального ускорения  .
.
Вектор  направлен от С к О.
направлен от С к О.
Модуль переносного касательного ускорения  . Вектор
. Вектор  направлен перпендикулярно кривошипу ОА в сторону
направлен перпендикулярно кривошипу ОА в сторону  .
.
Модуль относительного ускорения 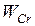 не известен, вектор
не известен, вектор  направлен вдоль кривошипа ОА. Зададимся произвольно его направлением от С к О.
направлен вдоль кривошипа ОА. Зададимся произвольно его направлением от С к О.
Кориолисово ускорение  . Модуль кориолисова ускорения
. Модуль кориолисова ускорения  . Вектор
. Вектор  направлен согласно правилу Жуковского (рис. 3.5).
направлен согласно правилу Жуковского (рис. 3.5).
Для определения величин  ,
,  следует решить векторное уравнение
следует решить векторное уравнение
 .(3.13)
.(3.13)
Запишем уравнение (3.13) в проекциях на оси декартовой системы координат  .
.
Система уравнений ускорений

Матричная форма уравнения
 ,
,
где  ;
;  ;
;  .
.
По изложенной методике выполнен кинематический анализ механизма в среде Mathcad (табл. 3.2).
Таблица 3.2
Результаты решения
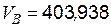
| 
| 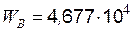
| 
|

| 
| 
| 
|

| – | 
| – |










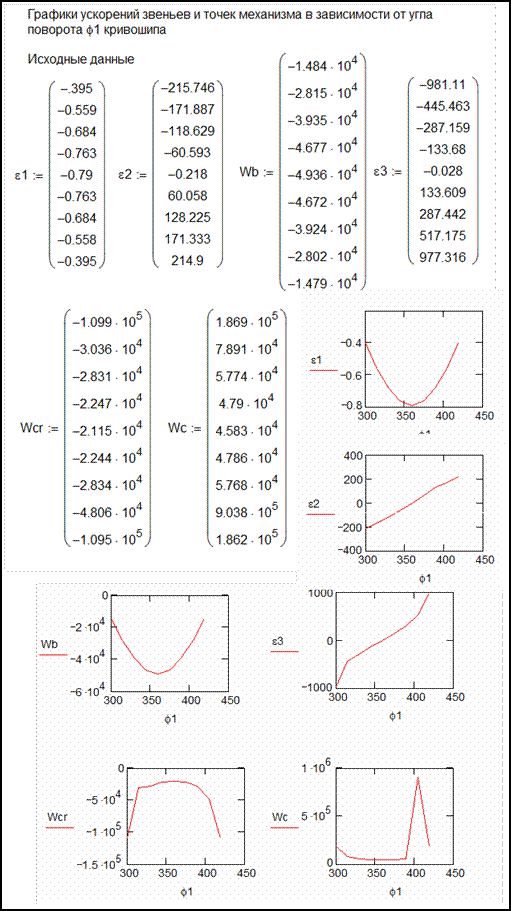
Кинематический анализ
Последнее изменение этой страницы: 2016-08-20
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...