
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Тема: Введение в теорию графов.
Тема: Введение в теорию графов.
Вопросы:
История возникновения теории графов.
Основные понятия теории графов.
Примеры использования теории графов.
История возникновения теории графов.
Мы частенько рисуем на листочках бумаги кружочки, квадратики, точки обозначая ими людей, населённые пункты, дела которые мы должны сделать и тому подобное, и соединяем их прямыми и ломаными линями, стрелочками которыми обозначаем связи между ними, отношения, последовательность действий и тому подобное.
Такие схемы встречаются всюду под разными названиями: социограммы (в психологии), симплексы (в топологии), электрические цепи (в физике), диаграммы организации (в экономике), сети коммуникаций, генеалогические деревья и т.д.
Д.Кёниг, предложил называть такие схемы "графами" и систематически изучать их свойства.
В совершенно различных дисциплинах приходится использовать аналогичные теоремы; так, понятие "матрицы инциденций", введенное Кирхгофом для изучения электрических цепей, было привлечено А.Пуанкаре в топологию при создании его "analysis situs"; понятие "точки сочленения", с давних пор известное в социологии, впоследствии появилось в электронике; все примеры такого рода перечислить невозможно. Чтобы можно было применять теорию графов в столь разнообразных областях, она должна быть в высшей степени абстрактной и формализованной.
В действительности такие основные понятия, как "цепь", "путь", "центр", будучи определены абстрактно, остаются в то же время неразрывно связанными с графической реальностью и легко распознаются, когда схема начерчена.
Рассматривая теорию графов, мы не ставим целью дать в руки математическое средство, наша задача сформировать общее представление прежде всего о её прикладных возможностях в теории организации управления.
Теория графов применяется в таких областях, как физика, химия, теория связи, проектирование вычислительных машин, электротехника, машиностроение, архитектура, исследование операций, кибернетика, общая теория систем, общая теория организаций, генетика, психология, социология, экономика, антропология и лингвистика и другие науки.
Эта теория тесно связана также со многими разделами математики, среди которых — теория групп, теория матриц, численный анализ, теория вероятностей, топология и комбинаторный анализ.
Теория графов служит математической моделью для всякой системы, содержащей бинарное отношение. Графы действуют притягательно и обладают эстетической привлекательностью благодаря их представлению в виде диаграмм. Хотя в теории графов много результатов, элементарных по своей природе, в ней также громадное изобилие весьма тонких комбинаторных проблем.
Теория графов «открывалась» независимо много раз: её с полным основанием можно считать разделом прикладной математики. В самом деле, наиболее раннее известное упоминание этой теории встречается в работах Эйлера, и хотя проблему, которой он занимался, можно рассматривать как обычную головоломку, псе же она возникла из практики.
Последующие переоткрытия теории графов Кирхгофом и Кэли также уходят своими корнями в реальную действительность. Изучение Кирхгофом электрических цепей привело к разработке им основных понятий и получению ряда теорем, касающихся деревьев в графах. В свою очередь Кэли подошел к исследованию деревьев, решая задачи перечисления органических изомеров.
Другой подход к графам, связанный с рассмотрением головоломок, был предложен Гамильтоном. После этого появилась знаменитая гипотеза четырёх красок, которая до сих пор пользуется широкой известностью.
В наше столетие также было чрезвычайно много переоткрытий теории графов. Упомянем кратко некоторые из них, придерживаясь хронологического порядка.
Задача о кёнигсбергских мостах
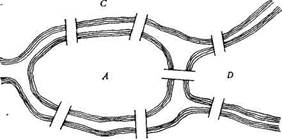
Отцом теории графов (так же как и топологии) является Эйлер (1707—1782), решивший в 1736 г. широко известную в то время задачу, называвшуюся проблемой кёнигсбергских мостов.
В городе Кенигсберге было два острова, соединенных семью мостами с берегами реки Преголя и друг с другом так, как показано на рисунке.
Задача состояла в следующем: найти маршрут прохождении всех четырех частей суши, который начинался бы с любой из них, кончался бы на этой же части и ровно один раз проходил по каждому мосту.
Легко, конечно, попытаться решить эту задачу эмпирически, производя перебор всех маршрутов, но все попытки окончатся неудачей.
Вклад Эйлера в решение этой задачи заключается в том, что он доказал невозможность такого маршрута.
В
Рисунок 1. Парк в городе Кенигсберге, 1736 г.

Рисунок 2. Граф к задаче о кенигсбергских мостах
Для доказательства того, что задача не имеет решения, Эйлер обозначил каждую часть суши точкой (вершиной), а каждый мост — линией (ребром), соединяющей соответствующие точки.
Получился «граф». Этот граф показан на рисунке 2., где точки отмечены теми же буквами, что и четыре части суши.
Утверждение о несуществовании «положительного» решения у этой задачи эквивалентно утверждению о невозможности обойти специальным образом граф, представленный на рисунке.
Отправляясь от этого частного случая, Эйлер обобщил постановку задачи и нашел критерий существования обхода (специального маршрута) у данного графа, а именно граф должен быть связным и каждая его вершина должна быть инцидентна (принадлежать) четному числу ребер.
Граф, показанный на рисунке, связный, но не каждая его вершина инцидентна (принадлежит) четному числу ребер.
Электрические цепи
В 1847 г. Кирхгоф разработал теорию деревьев для решения совместной системы линейных алгебраических уравнений, позволяющую найти значение силы тока в каждом проводнике (дуге) и в каждом контуре рассматриваемой электрической цепи.
Будучи физиком по образованию, он подходил к решению задач как математик. Абстрагируясь от электрических схем и цепей, которые содержат сопротивления, конденсаторы, индуктивности и т. д., он рассматривал соответствующие комбинаторные структуры, содержащие только вершины и связи (ребра или дуги), причем для связей не нужно указывать, каким типам электрических элементов они соответствуют.
Таким образом, в действительности Кирхгоф заменил каждую электрическую цепь соответствующим ей графом и показал, что для решения системы уравнений необязательно рассматривать в отдельности каждый цикл графа электрической цепи.


Рисунок 3. Сеть N, соответствующий ей граф G.
Вместо этого он предложил простую, но эффективную методику (ставшую позднее стандартной процедурой), в соответствии с которой достаточно ограничиться только независимыми простыми циклами графа, определяемыми любым из его «остовных деревьев». На рисунке 3 дан пример электрической цепи N, соответствующего ей графа G.
Химические изомеры
Занимаясь чисто практическими задачами органической химии, Кэли в 1857 г. открыл важный класс графов, называемых деревьями.
Он стремился перечислить изомеры предельных (насыщенных) углеводородов Сn Н2n+2 с данным числом n атомов углерода; рисунок 4.

Рисунок 4. Изобутан
В социальной психологии.
В 1936 г. психолог Курт Левин высказал предположение, что «жизненное пространство» индивидуума можно представить с помощью планарной карты 1).
На такой карте области представляют различные типы деятельности человека, например, то, что он делает на работе, дома, или же его хобби.


1) 2)
Рисунок 5. Карта и соответствующий ей граф.
Подчеркнем, что К.Левин фактически имел дело с графами, как это видно из рисунка 5.
Эта точка зрения привела психологов Научно-исследовательского центра групповой динамики к другой психологической интерпретации графа, в которой люди представляются вершинами, а их отношения — ребрами. Такими отношениями являются, например, любовь, ненависть, общение, подчинение.
Предположение Левина относится только к планарным картам, поскольку он всегда рисовал свои рисунки на плоскости. В последствии идея К.Левина была развита в социометрических процедурах.
В теории организаций
Графы могут быть представлены не только в строгой классической форме. Так жизненный цикл компании И.Адизеса представлен следующим форме.

Рисунок 6. Жизненный цикл компании
Функциональная организационная структурапостроена по принципу распределения функций внутри организации и создания сквозных подструктур по управлению функциями.

Производственные подразделения
Рис. Функциональная организационная структура
Таким образом, необходимость специальной общей теории, применимой в любой сфере жизнедеятельности человека была обусловлена потребностями практики.
Такой теорией стала «Теория графов».
Основные понятия теории графов
Начнём с определения, однозначного определения теория графов не имеет, ниже представлены три определения, но существуют и другие.
Теория графов - раздел дискретной математики, исследующий свойства конечных множеств с заданными отношениями между их элементами.
Теория графов - раздел математики, особенность которого - геометрический подход к изучению объектов
Теория графов - математический язык для формализованного определения понятий, связанных с анализом и синтезом структур систем и процессов.
Мы остановимся на следующем:
Рисунок 7. Вершина, рёбро и дуга.
Обозначим граф буквой G=(V,E).

Рисунок 8. Граф Ga. Рисунок 9. Граф Gb
На рисунках 8 и 9 представлены графы Ga - у которого V - количество вершин равно 4,
а E – количество рёбер равно 3 b и граф Gb - у которого V - количество вершин равно 4,
а E – количество дуг равно 3 b.
Рисунок 10.
Для орграфа на рис.10 входящие степени вершин 1,2,3,4,5 равны соответственно 0,1,1,1,0, исходящие - 2,0,0,1,0.
Степени вершин, получаемые сложением входящих и исходящих степеней равны 2,1,1,2,0. Таким образом, вершина 5 - изолированная.

Рисунок 11. Петля.
Петля- ребро принадлежащее (инцидентное) одной вершине (единственной). Рисунок 11.
Петля –ребро, дуга, соединяющее вершину саму с собой.
Петля- ребро оба конца которого принадлежат одной и той же вершине.
Может быть несколько петель
Псевдограф — граф, содержащий петли
Если одну пару вершин соединяют два или более ребер, то такие ребра называют кратными.
Граф называется простым, если он не содержит ни петель, ни кратных ребер, иначе граф называется мультиграфом. (В некоторых источниках граф с кратными ребрами называют мультиграфом, с петлями - псевдографом.)
Простой граф, любая пара вершин которого соединена ребром, называется полным. В полном графе n * (n-1)/2 ребер.
Граф называется полным если он содержит максимально возможное количество рёбер.
Граф называется разреженным, если общее количество ребер значительно меньше их возможного количества.


Рисунок 12. Полный граф. Рисунок 13. Разреженный граф.
Путь в орграфе
Путём называется такая последовательность вершин в ориентированном графе при которой конец входящей дуги является началом исходящей дуги.
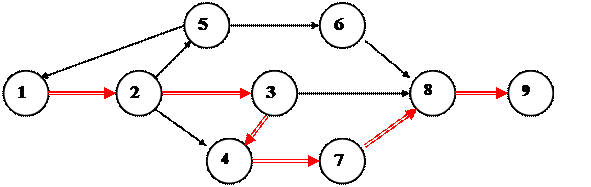
Рисунок 14. Путь в орграфе.
Путь в орграфе — это последовательность вершин v1, v2, …, vn, для которой существуют дуги e1 -> e2, e2 -> e3, …, en-1 – vn> en.
Говорят, что этот путь начинается в вершине v1, проходит через вершины v2, v3, …, vn-1, и заканчивается в вершине vn.
На рисунке 14. путь это последовательность вершин 1,2,3,4,7,8,9.
Длина пути — это количество дуг, составляющих путь. На рисунке 14. длина пути равна 6.
Вершина 1- начало пути, вершина 9 - конец пути
Путь называется простым, если он содержит каждую из вершин не более одного раза.
Цикломназывается путь из некоторой вершины в эту же вершину, содержащий хотя бы одно ребро. На рисунке 14. Путь 1, 2, 5, 1. – цикл.
Цикл простой, если в нем нет повторяющихся вершин (за исключением начальной (конечной), которая является первой и последней вершиной пути).
Цепь – последовательность смежных вершин. Или множество рёбер (в неориентированном графе) которые можно расположить так, что конец одного ребра является началом другого.
Граф дерево
Граф без циклов называется деревом.
Важный класс графов составляют ориентированные деревья.
Во многих приложениях дерево удобно считать ориентированным графом. Как показывает пример на рисунке 15, «превратить» дерево в ориентированный граф несложно.

Рисунок 15. Граф дерево.
Дадим соответствующее определение.
Определение. Ориентированный граф G называется ориентированным деревом, если выполняются следующие условия:
1. существует в точности одна вершина (корень), степень захода которой равна нулю;
2. степень захода любой вершины, кроме корня, равна единице;
3. для любой вершины v, отличной от корня, существует путь из корня в эту вершину;
Граф называется двудольным, если множество его вершин V можно разбить на непересекающиеся подмножества V1 и V2 так, что никакие две вершины одного подмножества не смежны. Пример двудольного графа на рис. 16.

Рисунок 16. Двудольный граф.
Если левое подмножество представить как необходимые виды работ, а правое как сотрудников обладающих компетенциями для выполнения этих видов работ.
Связи - это компетенции, которыми обладают сотрудники.
Мы получаем граф, который наглядно представляет, кто какие виды работ может выполнять.
На основе этого графа можно определять заработную плату с учётом объёма и разнообразия компетенций сотрудников.
Этот граф наглядно показывает, что увеличение объёма и разнообразия компетенций сотрудников позволить обеспечить надёжность и устойчивость организации.
Так в Советский период на всех предприятиях было развёрнуто «движение смежников», стимулировалось овладение смежной специальностью. Это объяснялось непрерывным ростом производства и нехваткой рабочих рук.
В современный период аналогичный принцип внедрён в компании Toyota под названием «Бережливое производство».
В 2002 г. руководство Toyota обратилось к «ведущим специалистам по технологиям производства компании с просьбой подумать над недостатками системы "бережливого производства" — той самой системы, принципы которой сделали Toyota предметом поклонения менеджеров во всем мире.
"Бережливое производство" подразумевает в первую очередь способность к гибкости, когда, например, один рабочий может выполнять самые разные задания.
Эта система оказалась более эффективной, чем американские сборочные линии, где сотрудник десятки лет выполняет одну-единственную специфическую работу.
Транспортные» задачи.
Транспортные коммуникации- вершинами графа являются пункты, а рёбрами дороги или дугами маршруты.
Информационные коммуникации –вершины графа источник информации, реципиенты, а дуги каналы коммуникации.
Сети снабжения – электроснабжения, газоснабжения, снабжение другими ресурсами. Вершины пункты производства и потребления, а дуги маршруты их доставки.
Управление проектами.
С точки зрения теории графов проект - совокупность операций и зависимостей между ними {сетевой график - см. ниже). Хрестоматийным примером является проект строительства некоторого объекта.
Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач управления проектами, получила название календарно-сетевого планирования и управления (КСПУ).
В рамках КСПУ решаются задачи определения последовательности выполнения операций и распределения ресурсов между ними, оптимальных с точки зрения тех или иных критериев (времени выполнения проекта, затрат, риска и др.).
Сетевая модель инновационного проекта.Сетевая модель инновационного проекта (от греч. grapho - пишу) - календарный график работ по реализации инновационного проекта, наглядно отражающий пути достижения инновационной цели. В ее основе лежит метод
сетевого планирования, использующий теорию графов.
3. Сетевое планирование.
Сетевое планирование – это комплекс графических и расчетных методов организационных мероприятий, обеспечивающих моделирование, анализ и динамическую перестройку плана выполнения сложных проектов и разработок [1].
Характерной особенностью таких проектов является то, что они состоят из ряда отдельных элементарных работ.
Они обусловливают друг друга так, что выполнение некоторых работ не может быть начато раньше, чем завершены некоторые другие.
Классическое представление задачи сетевого планирования показано на рис.18. Основными понятиями сетевых моделей являются понятия работы, события и пути.
Дуги -это работа,некоторый процесс, имеющий протяженность во времени, требующий затрат каких-либо ресурсов и приводящий к достижению определенного результата (обозначается стрелками).
Вершина –это событие – это момент времени, когда завершаются одни работы и начинаются другие (обозначается кружком).
 Рисунок 18.
Рисунок 18.

Рисунок 19.
Путь – это любая последовательность работ (дуг) в сетевом графике, в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы. Различают:
· полный путь – путь от исходного до завершающего события;
· критический путь – максимальный по продолжительности полный путь;
· подкритический путь – полный путь, ближайший по длительности к критическому пути.
Таблица. Основные типы неформальных структур - представлена виде графов.
| Число членов группы | Номер типа структуры. | |||||

| ||||||

| ||||||
 
| ||||||
   
| ||||||
     
| ||||||
      
|
Тема: Введение в теорию графов.
Вопросы:
Последнее изменение этой страницы: 2016-08-28
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...