Множество всех центральных вершин графа называется его центром.

Пример: Значит, d(G)=4; r(G)=2

Центральная вершина x5

Определение:

Маршрут, цепь и цикл в графе называются простыми, если они проходят через любую из вершин не более одного раза.

Определение:

Неориентированный граф называется связным, если между любыми его двумя вершинами есть маршрут.

Пример:

Связный граф.

У несвязного графа не все вершины можно соединить цепями с данной вершиной V1.Те вершины, которые можно соединить с вершиной V1 , и все инцидентные им ребра образуют связную компоненту вершины V1. Таким образом, весь граф распадается на связные компоненты, не соединенные между собой ни ребрами, ни цепями.

На рис. 12 изображен граф, состоящий из четырех связных компонент, одна из которых представляет собой изолированную вершину.

Этот граф может соответствовать, например, карте дорог группы островов, где каждый остров имеет связную систему дорог. В теории графов обычно предполагают, что рассматриваемый граф является связным, так как иначе можно отдельно изучать свойства каждой из его связных компонент.

Примем без доказательства следующую теорему:

Теорема 3.

Для того, чтобы связный граф G являлся простым циклом, необходимо и достаточно, чтобы каждая его вершина имела степень, равную 2.

Определение:

Ребро связного графа G называется мостом, если после его удаления G станет несвязным и распадается на два связных графа G1 и G2.

Сформулируем теорему:

Теорема 4.

Ребро графа является мостом, тогда и только тогда, когда не принадлежит ни одному циклу.

Пример:

Граф G с мостами ВС и СЕ.

Двудольные графы.

Определение:

Неориентированный граф G(V, E) называется двудольным, если множество его вершин может быть разбито на такие два непересекающиеся подмножества V1 и V2 ,что каждое ребро графа G имеет один конец в V1, а другой в V2.

Например,

Множество вершин V1 неориентированного графа составляют вершину {a, b, c, d, e}, а множество вершин V2 {f, g, j, k}.

Граф G называется полным двудольным, если каждая вершина множества Vё связана ребрам с каждой вершиной множества V2.

Например:

Граф Gможно изображать по-разному.

Совсем не обязательно изображать его ребра прямолинейными, вершины графа могут располагаться на плоскости произвольно.

Определение:

Графы G1 и G2 называются изоморфными, если существует взаимно-однозначное соответствие между их ребрами и их вершинами, причем соответствующие ребра соединяют соответствующие вершины.

Иными словами, можно так переобозначить вершины графа G1, что в новыхобозначениях вершины и ребра будут совпадать со вторым графом G2 , причем кратным ребрам первого графа будут соответствовать кратные ребра второго графа такой же кратности.

Важно, что изоморфизм графов является отношением эквивалентности.

На практике такие различные по внешним признакам изоморфные графы не различают, рассматривая их с точностью до изоморфизма.

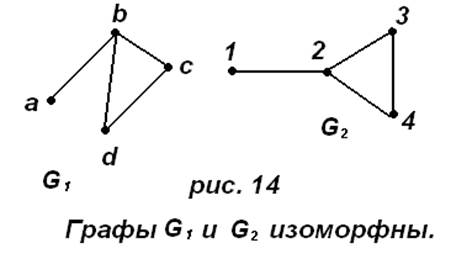
Нередко приходится решать вопрос, являются ли два графа изоморфными. Иногда сразу же видно, что это не так. Например, если у них разное количество вершин (рис. 15) или ребер (рис.16).

Однако показать неизоморфизм графов (рис. 17) более сложно.

Например, можно заметить, что в графе G1 существует маршрут из 8 смежных ребер с началом и концом в вершине 1, а в графе G2 такого маршрута нет.

(1, 2), (2, 3), (3, 4), (4, 8), (8, 7),(7, 6), (6, 5), (5, 1)

Методику проверки графов на изоморфизм рассмотрим при изучении ориентированных графов.

Плоские графы.

Определение:

Граф G называется плоским, если существует изоморфный ему граф G´, в изображении которого на плоскости ребра пересекаются только в вершинах.

Например: графы G на рис. 18 является плоским, т.к. существует изоморфный ему граф G´.

Иными словами, у плоского графа никакие два ребра не имеют общих точек, кроме вершин.

Определение: