
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Изучение работы мультиплексоров
Краткие сведения из теории
Мультиплексор - комбинационная логическая схема, представляющая собой управляемый переключатель, который подключает к выходу один из информационных входов данных. Номер подключаемого входа равен числу (адресу), определяемому комбинацией логических уровней на входах управления. Кроме информационных и управляющих входов, схемы мультиплексоров содержат вход разрешения, при подаче на который активного уровня мультиплексор переходит в активное состояние. При подаче на вход
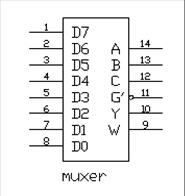 Рис. 2.1 Рис. 2.1
| разрешения пассивного уровня мультиплексор перейдет в пассивное состояние, для которого сигнал на выходе сохраняет постоянное значение независимо от значений информационных и управляющих сигналов.Число информационных входов у мультиплексоров обычно 2, 4, 8 или 16. На рис. 2.1 представлен мультиплексор 8x1 с инверсным входом разрешения G, прямым Y и инверсным W-выходами (  ). ).
|
Уравнение работы мультиплексора
Функционирование мультиплексора, представленного на рис. 2.1, описывается характеристическим уравнением, связывающим сигнал на выходе (Y) с разрешающим (G), входными информационными (D0 … D7) и управляющими (А, В, С) сигналами:

Как видно из уравнения, на мультиплексоре можно реализовать логические функции, для чего нужно определить, какие сигналы и логические константы следует подавать на входы мультиплексора.
Реализация заданной функции с помощью мультиплексора
Логическая функция n переменных определена для  комбинаций значений переменных. Это позволяет реализовать функцию n переменных на мультиплексоре, имеющем n управляющих и
комбинаций значений переменных. Это позволяет реализовать функцию n переменных на мультиплексоре, имеющем n управляющих и  информационных входов. В этом случае каждой комбинации значений аргументов соответствует единственный информационный вход мультиплексора, на который подается значение функции.
информационных входов. В этом случае каждой комбинации значений аргументов соответствует единственный информационный вход мультиплексора, на который подается значение функции.
Например, требуется реализовать функцию

Эта функция определена только для 8 комбинаций значений переменных, поэтому для её реализации можно использовать мультиплексор 8x1 с тремя управляющими входами. Составим таблицу истинности функции (табл.2.1).
| Таблица 2.1 | ||||
| DN | c | b | a | F1 |
| D0 | ||||
| D1 | ||||
| D2 | ||||
| D3 | ||||
| D4 | ||||
| D5 | ||||
| D6 | ||||
| D7 |
Из таблицы видно, что для реализации функции на мультиплексоре необходимо подать на информационный вход мультиплексора с номером N сигнал, значение которого равно соответствующему значению функции F1, т.е. на входы D0, D1, D5, D7 следует подать уровень логической единицы, а на остальные - уровень логического нуля. Таким образом, при подаче комбинации логических уровней на управляющие входы мультиплексора к его выходу подключится вход, значение сигнала на котором равно соответствующему значению функции. Схемная реализация приведена на рис. 2.2.

Рис. 2.2
При реализации логических функций на информационные входы можно подавать не только константы, но и изменяющиеся входные сигналы. Так, например, рассмотрим другой способ реализации функции F1, рассмотренной выше. Для этого минимизируем выражение функции  .
.
Составим таблицу истинности функции в зависимости от значений переменных а и b (табл. 2.2).
| Таблица 2.2 | |||
| N | b | A | F1 |
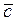
| |||
| с |
Заданную такой таблицей функцию реализуют, как и в предыдущем случае, подав на вход с номером N сигнал, значение которого соответствует значению функции F1. В данном случае сигналы с и  , соответствующие переменной с, подаются на информационные входы, как указано в таблице истинности. При этом сокращается число управляющих входов.
, соответствующие переменной с, подаются на информационные входы, как указано в таблице истинности. При этом сокращается число управляющих входов.
Схемная реализация такого способа задания функции представлена на рис. 2.3. Так как используются только два адресных входа, управляющий вход С можно заземлить. При этом состояние информационных входов D4...D7 безразлично. Уровень сигнала на выходе схемы определяется комбинацией уровней сигналов в точках А, В, С, соответствующих переменным а, b, с. Схема рис. 2.3 по существу представляет собой мультиплексор 4x1 с двумя управляющими и четырьмя информационными входами.

Рис. 2.3
Если функцию можно представить в виде произведения одночлена на многочлен, то её также можно реализовать при помощи мультиплексора. Как следует из уравнения мультиплексора, сигнал, соответствующий одночлену, нужно подать на вход разрешения. Например, требуется реализовать функцию F2, описываемую следующим выражением:
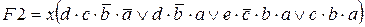 .
.
При реализации данной функции на мультиплексоре сигнал, соответствующий переменной x, следует подать на его разрешающий вход. Рассмотрим, какие сигналы необходимо подать на управляющие входы мультиплексора. Выражение в скобках можно рассматривать как некоторую функцию f пяти переменных: а, b, с, d, е, из которых наиболее часто используются переменные a, b и с. Поэтому сигналы, соответствующие этим переменным, нужно подать на управляющие входы мультиплексора.
Определим, какие сигналы следует подать на информационные входы, чтобы реализовать функциюf. Для этого составим таблицу истинности функции в зависимости от значений переменных a, b и с(табл. 2.3).
| Таблица 2.3 | ||||
| N | C | b | a | f |
| d | ||||
| e | ||||
| d | ||||
Из таблицы видно, что на входы с номерами N = 0, 2, 4, 6 нужно подать уровень логического нуля. Сигнал, соответствующий переменной d, нужно подать на входы с номерами N = 1, 5, сигнал, соответствующий переменной е, - на вход с номером 3. Схемная реализация представлена на рис. 2.4.
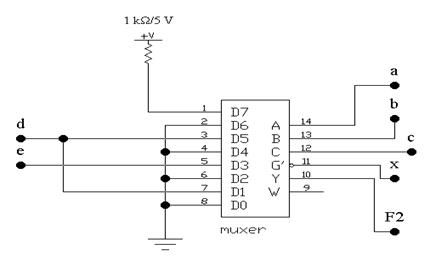
Рис. 2.4
ЗАДАНИЕ К КОНТРОЛЬНОЙ РАБОТЕ № 2
1. Разработать, собрать и проверить работу схемы на основе мультиплексора 8×1, реализующую заданную логическую функцию Y. Варианты задач указаны ниже.
| Вариант 1 | 
|
| Вариант 2 | 
|
| Вариант 3 | 
|
| Вариант 4 | 
|
| Вариант 5 | 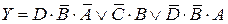
|
| Вариант 6 | 
|
| Вариант 7 | 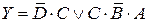
|
| Вариант 8 | 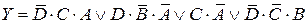
|
| Вариант 9 | 
|
| Вариант 10 | 
|
| Вариант 11 | 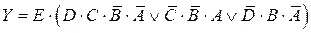
|
| Вариант 12 | 
|
| Вариант 13 | 
|
| Вариант 14 | 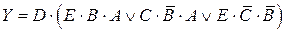
|
| Вариант 15 | 
|
| Вариант 16 | 
|
| Вариант 17 | 
|
| Вариант 18 | 
|
| Вариант 19 | 
|
| Вариант 20 | 
|
Последнее изменение этой страницы: 2017-07-07
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...