
Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Часть 1. Основы статистической динамики судовых конструкций
ПРИЛОЖЕНИЕ. Основные понятия теории вероятностей 124
ВВЕДЕНИЕ
Внедрение вероятностных методов при выполнении расчетов судовых конструкций начато в середине прошлого столетия. Значительный вклад в развитие таких методов для исследований динамики, надежности и работоспособности механических систем внесли работы В.В. Екимова, В.В.Болотина и А.А. Курдюмова. Использованию вероятностных методов в исследовательской практике судостроения посвящены работы Г.В. Бойцова, А.И.Вознесенского, А.В. Герасимова, Ю.Н. Ипатовцева, В.В. Козлякова, Я.И. Короткина, Ю.Н. Нецветаева, А.И. Максимаджи, Н.Н. Рахманина, А.А. Свешникова, Г.А.Фирсова и многих других авторов.
Опыт первого десятилетия по применению вероятностных методов в отечественной практике изложен в известной монографии В.В. Екимова “Вероятностные методы в строительной механике корабля” (1966 г.), не потерявшей актуальности до сих пор. К этой теме неоднократно обращались авторы учебников и монографий по прочности и надежности корабля, однако в этих весьма полезных работах пока не достигнута столь высокая степень обобщения материала, как в труде В.В. Екимова. Вместе с тем за последние десятилетия накоплен обширный исследовательский материал в области использования подобных методов, содержащийся в многочисленных статьях и не повергнутый пока серьезному обобщению. В частности, имеются результаты новых исследований в следующих направлениях:
- разработка новых математических моделей для описания ветрового волнения;
- создание новых методов вероятностного анализа нелинейной качки и нелинейных колебаний судовых конструкций;
- разработка способов анализа волновой вибрации судового корпуса;
- разработка новых методов оценки показателей безотказности, ресурса, надежности и эксплуатационной безопасности;
- создание специальных приемов вероятностной оценки внешних нагрузок и обеспечения прочности судов, имеющих эксплуатационные ограничения по интенсивности волнения и маршрутам передвижения;
- контроль технического состояния конструкций (включая коррозионный износ) и учет его при обеспечении прочности и эксплуатационной безопасности судов;
- учет особенностей свойств материалов при выборе принципов проектирования конструкций и назначении практических приемов обеспечения их эксплуатационной безопасности.
Эти обстоятельства дают основание считать актуальным написание новой монографии, посвященной описанию и обобщению вероятностных методов. При этом авторы настоящей монографии осознавали необходимость охвата достаточно широкого круга полученных в последние десятилетия результатов исследований, так и доступного его изложения. При стремлении обеспечить такую доступность, авторы ориентировались на уровень подготовки инженеров и магистров, выпускаемых ВУЗАми с хорошей общетехнической подготовкой (что представляется целесообразным в условиях смены поколений, ожидаемой в ближайшем будущем в исследовательских организациях и конструкторских бюро судостроения). Исходя из таких соображений, во-первых, значительная часть книги посвящена общим вопросам использования вероятностных методов (включая их математическое обоснование), и, во-вторых, круг прикладных вопросов ограничен типами судов, строительство которых предусматривается в ближайшем будущем в больших количествах. При этом ввиду ограниченности объема книги пришлось отказаться от изложения проблем, относящихся к скоростным судам и средствам освоения океанского шельфа.
В связи с изложенным, к кругу читателей книги могут быть отнесены студенты старших курсов кораблестроительных ВУЗов, а также специалисты НИИ и конструкторских бюро, работающие над проблемами конструирования, обеспечения прочности и надежности судов.
Часть 1. Основы статистической динамики судовых конструкций
Спектральная плотность
При спектральном представлении стационарного СП и каноническом разложении корреляционной функции выше использовалось разложение функций в ряд Фурье. Этот ряд представляет собой разложение периодической функции по тригонометрическим функциям на некотором конечном временном интервале от —Т до +T. При наличии периодичности функции и конечности временного интервала число членов ряда конечно, а частоты гармоник  образуют дискретный спектр. Это разложение можно обобщить и на случай непериодической функции. Приближенный метод разложения в ряд Фурье для непериодической функции состоит в применении предельного перехода при
образуют дискретный спектр. Это разложение можно обобщить и на случай непериодической функции. Приближенный метод разложения в ряд Фурье для непериодической функции состоит в применении предельного перехода при  т.е. непериодическую функцию рассматривают как периодическую при неограниченно возрастающем периоде.
т.е. непериодическую функцию рассматривают как периодическую при неограниченно возрастающем периоде.
Представив (1.7) в формулу (1.6) запишем разложение корреляционной функции в ряд Фурье в виде
 . (1.18)
. (1.18)
Перейдем к пределу, устремляя Т к бесконечности и полагая 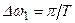 . Величина
. Величина 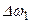 есть частотный интервал между соседними гармониками, частоты которых равны
есть частотный интервал между соседними гармониками, частоты которых равны  и
и  . При предельном переходе положим, что при
. При предельном переходе положим, что при 
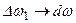 и
и 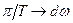 , а
, а  , где
, где 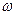 — текущая частота, изменяющаяся непрерывно. Сумма в уравнении (1.18) перейдет в интеграл, тогда
— текущая частота, изменяющаяся непрерывно. Сумма в уравнении (1.18) перейдет в интеграл, тогда
 (1.19)
(1.19)
Введем обозначение
 (1.20)
(1.20)
Тогда (1.19) примет вид
 (1.21)
(1.21)
Зависимости (1.20) и (1.21) часто называют формулами Винера-Хинчина. Во многих практических задачах корреляционная функция может быть найдена из данных эксперимента, а спектральная плотность процесса—по зависимости (1.20).
Функция  , представимая в форме (1.19), имеет непрерывный спектр. Если ряд Фурье (1.18) дает возможность представить периодическую функцию в виде суммы бесконечного числа косинусоид с частотами, имеющими дискретные значения, то интеграл Фурье (1.21) представляет непериодическую функцию в виде суммы синусоид с непрерывной последовательностью частот. Спектр периодической функции можно изобразить графически (рис. 1.3.). Каждому дискретному значению частотырис. 1.2 (частоты
, представимая в форме (1.19), имеет непрерывный спектр. Если ряд Фурье (1.18) дает возможность представить периодическую функцию в виде суммы бесконечного числа косинусоид с частотами, имеющими дискретные значения, то интеграл Фурье (1.21) представляет непериодическую функцию в виде суммы синусоид с непрерывной последовательностью частот. Спектр периодической функции можно изобразить графически (рис. 1.3.). Каждому дискретному значению частотырис. 1.2 (частоты 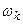 гармоник ряда Фурье) соответствует определенное значение коэффициента ряда Dk. Спектр, показанный на рис. 1.8, называют дискретным или линейчатым.
гармоник ряда Фурье) соответствует определенное значение коэффициента ряда Dk. Спектр, показанный на рис. 1.8, называют дискретным или линейчатым.

Рис. 1.8. Линейчатый спектр СП.
Рассмотрим теперь спектр непериодической функции. В результате предельного перехода от ряда к интегралу Фурье (от конечного интервала времени T к бесконечному) интервалы между отдельными спектральными линиями неограниченно сокращаются, вертикальные линии (см. рис. 1.3) все больше сближаются. Амплитуда Dk каждой отдельной гармоники с частотой 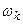 уменьшается и в пределе становится бесконечно малой.
уменьшается и в пределе становится бесконечно малой.
Введем обозначение
Dk/Dw1 = 
Величина  Dw1 = Dk представляет собой ту часть общей дисперсии стационарного СП Х(t), которая приходится на k-ю гармонику. С увеличением периода разложения (T® ¥) ступенчатая (постоянная на любом частотном интервале
Dw1 = Dk представляет собой ту часть общей дисперсии стационарного СП Х(t), которая приходится на k-ю гармонику. С увеличением периода разложения (T® ¥) ступенчатая (постоянная на любом частотном интервале  ) функция
) функция  не будет постоянно уменьшаться (как величины Dk и Dw1), а будет неограниченно приближаться к предельной плавной кривой Sx(w), которая представляет собой плотность распределения дисперсий по частотам непрерывного спектра.
не будет постоянно уменьшаться (как величины Dk и Dw1), а будет неограниченно приближаться к предельной плавной кривой Sx(w), которая представляет собой плотность распределения дисперсий по частотам непрерывного спектра.
Таким образом,
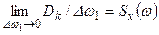 . (1.22)
. (1.22)
Поэтому функцию  , определяемую как косинус-преобразование Фурье (1.20) корреляционной функции
, определяемую как косинус-преобразование Фурье (1.20) корреляционной функции  , называют спектральной плотностью (или просто спектром)процесса
, называют спектральной плотностью (или просто спектром)процесса 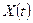 .
.
Спектральная плотность Sx(w) стационарного СП обладает следующими свойствами:
1°. Она является неотрицательной функцией частоты w :
Sx(w) ³ 0.
Это следует из выражения (1.22), так как предел отношения двух неотрицательных величин Dk ³ 0 и Dw > 0 не может быть отрицательным.
2°. Интеграл от спектральной плотности в пределах от 0 до ¥ равен дисперсии стационарного СП:
 . (1.23)
. (1.23)
Это следует из равенства (1.21):
 .
.
Графически эти два свойства спектральной плотности отображены на рис. 1.9. Кривая Sx(w) спектральной плотности расположена не ниже оси абсцисс, а площадь, ограниченная этой кривой сверху, осью абсцисс снизу и осью ординат слева, равна дисперсии Dx (заштрихованная фигура на рис. 1.4).

Рис. 1.9. Спектральная плотность СП.
По аналогии с нормированной корреляционной функцией
rx(t) = kx(t)/kx(0) = kx(t)/Dx (1.24)
вводится в рассмотрение нормированная спектральная плотность стационарного СП:
sx(w) = Sx(w)/Dx . (2.25)
Нормированная КФ и нормированная спектральная плотность связаны между собой преобразованием Фурье:
 (1.26)
(1.26)
Определим понятие спектральной плотности стационарного СП в комплексной форме. Для этого перепишем каноническое разложение КФ (1.15) в виде
 (1.27)
(1.27)
где  .
.
Подставляя в (1.27) выражение для коэффициента  , получим
, получим
 (1.28)
(1.28)
Осуществим аналогичный описанному выше предельный переход, устремляя Т к бесконечности и полагая  . При таком переходе положим, как и ранее, что при
. При таком переходе положим, как и ранее, что при 
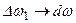 и
и 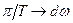 , а
, а  .Сумма в уравнении (1.28) перейдет в интеграл, тогда
.Сумма в уравнении (1.28) перейдет в интеграл, тогда
 (1.29)
(1.29)
где  (1.30)
(1.30)
Функция  называется спектральной плотностью стационарного СП в комплексной форме. Ее называют также двусторонней спектральной плотностью. В отличие от обычной (односторонней) спектральной плотности
называется спектральной плотностью стационарного СП в комплексной форме. Ее называют также двусторонней спектральной плотностью. В отличие от обычной (односторонней) спектральной плотности 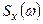 , она определена не только в области положительных частот
, она определена не только в области положительных частот 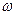 , но и в отрицательной области (рис. 1.10). Легко показать, что при положительных
, но и в отрицательной области (рис. 1.10). Легко показать, что при положительных 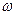 выполняется соотношение
выполняется соотношение  .
.

Рис. 1.10. Односторонняя ( 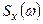 ) и двухсторонняя (
) и двухсторонняя ( ) спектральные плотности.
) спектральные плотности.
Двусторонние спектральные плотности (также как и разложения процесса X(t) и  в комплексной форме) удобны при выполнении теоретических выкладок, но при решении прикладных задач, как правило, эффективнее применять односторонние спектры.
в комплексной форме) удобны при выполнении теоретических выкладок, но при решении прикладных задач, как правило, эффективнее применять односторонние спектры.
Двусторонняя спектральная плотность  стационарного СП обладает тремя свойствами: 1)
стационарного СП обладает тремя свойствами: 1)  при любых (положительных и отрицательных) значениях
при любых (положительных и отрицательных) значениях 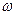 ; 2)
; 2) 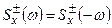 (четная функция); 3) интеграл от спектральной плотности в бесконечных пределах равен дисперсии СП
(четная функция); 3) интеграл от спектральной плотности в бесконечных пределах равен дисперсии СП
 .
.
Формулы Винера-Хинчина (1.29) и (1.30), а также их аналоги (1.21) и (1.20) являются важнейшими в спектральной теории.
Сложение случайных процессов
В приложениях часто встречаются случайные процессы, являющиеся результатом сложения нескольких случайных функций. Например, перемещения в произвольной точке судна, обусловленные стационарным случайным процессом морского волнения, представляют сумму перемещений при отдельных видах качки (вертикальной, килевой, бортовой и др.), рассматриваемых, в ряде случаев, как стационарные нормальные процессы.
Для определения характеристик суммарного, процесса необходимо знание так называемой взаимной корреляционной функции (или корреляционной функции связи).
Пусть

где a, b — неслучайные множители. Тогда математическое ожидание будет определяться по формуле
 (1.33)
(1.33)
где тx и тy—математические ожидания функций X (t) и Y(t). Корреляционная функция суммарного процесса Z(t)
 (1.34)
(1.34)
Величина  называется взаимной корреляционной функцией; она равна корреляционному моменту соответствующих сечений случайных функций X(t) и Y(t)
называется взаимной корреляционной функцией; она равна корреляционному моменту соответствующих сечений случайных функций X(t) и Y(t)
 (1.35)
(1.35)
Отметим, что взаимная корреляционная функция процессов X (t) и Y(t) не равна взаимной корреляционной функции Y(t)и X (t)

Если переставить местами аргументы, то взаимные корреляционные функции равны
 (1.36)
(1.36)
В ряде случаев вводится нормированная взаимная корреляционная функция
 (1.37)
(1.37)
где  и
и  — стандарты функций X(t) и Y(t).
— стандарты функций X(t) и Y(t).
Для стационарных случайных функций вместо (2.34) получим
 (1.38)
(1.38)
Переходя к дисперсии случайного процесса Z(t), положим в (2.38) 
 (1.39)
(1.39)
Здесь Rxy(0) есть не что иное, как корреляционный момент системы случайных величин X(t) и Y(t):
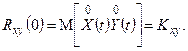
Корреляционный момент  часто находят по известной взаимной спектральной плотности процессов X(t) и Y(t), которая, по определению, равна преобразованию Фурье взаимной корреляционной функции
часто находят по известной взаимной спектральной плотности процессов X(t) и Y(t), которая, по определению, равна преобразованию Фурье взаимной корреляционной функции  :
:
 (1.40)
(1.40)
Корреляционный момент  выражается через взаимную спектральную плотность
выражается через взаимную спектральную плотность  так
так
 (1.41)
(1.41)
Обобщая зависимость (1.39) на случай сложения большого числа случайных функций

можно получить
 (1.42)
(1.42)
Если взаимная корреляционная функция равна нулю, то соответствующие случайные функции называются некоррелированными. В этом случае  при
при  и вместо (1.42) получим
и вместо (1.42) получим
 (1.43)
(1.43)
Заметим здесь, что процессы, получаемые при сложении гауссовских процессов (также как и линейных действиях над ними) являются снова гауссовскими. Так, например, если компонента напряженного состояния в какой-либо точке конструкции является суммой коррелированных и центрированных гауссовских процессов, порождаемых воздействием нескольких изменяющихся во времени сил Qj, то распределение ординат этой компоненты подчиняется нормальному закону, а для определения единственного параметра распределения суммарного процесса пригодны приведенные здесь формулы.
Группы волн
При всей кажущейся хаотичности и неупорядоченности последовательности сменяющих друг друга волн в ней существует определенная закономерность. Коэффициент корреляции между высотами соседних волн колеблется от 0,6 до 0,3 [22] в зависимости от типа и интенсивности волнения; для волн, отделенных друг от друга одной волной, коэффициент корреляции составляет 0,3—0,1, а двумя волнами—0,2—0,05 [22]. Помимо статистической закономерности, выражающейся в коррелированности высот соседних волн, имеются также определенные топологические и структурные закономерности нерегулярного волнения.
В ряду нескольких волн, постепенно нарастающих по высоте, проходит особенно высокая волна, после которой следуют волны уменьшающейся высоты. Через некоторое время аналогичная картина повторяется, т. е. волны проходят группами. Группы волн—одна из характерных черт волнения, проявляющаяся в циклической смене последовательностей волн, состоящих из достаточно высокой волны, которой предшествуют и за которой следуют волны меньшей высоты (рис. 2.13).

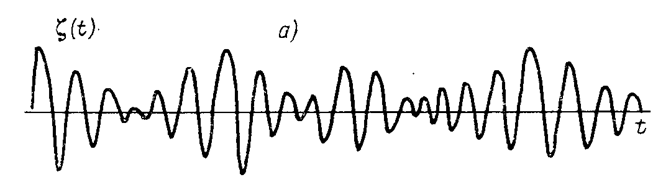
Рис. 2.13. Параметры волнового пакета.
До настоящего времени не существует общепринятого определения понятия группы волн, хотя с существованием групповой структуры приходится считаться при расчетах волновых воздействий на суда и сооружения.
Исследование групповой структуры по волнограммам (и по волновым профилям) представляет интерес прежде всего при анализе тех процессов силовых воздействий на объекты (на суда, плавучие и стационарные буровые установки), амплитуды которых нелинейно связаны с амплитудами волн. В практике судостроительных расчетов группы волн рассматриваются как последовательность подряд идущих волн, в которой наибольшая высота  превышает среднюю высоту
превышает среднюю высоту  , рассчитанную по всей последовательности волн, а слева и справа от
, рассчитанную по всей последовательности волн, а слева и справа от  располагаются волны с меньшими высотами; наименьшие волны
располагаются волны с меньшими высотами; наименьшие волны  в такой последовательности, имеющие высоту менее
в такой последовательности, имеющие высоту менее  , являются границей групп.
, являются границей групп.
Результаты вычисления среднего числа волн  в группе по записям ветровых волн показали, что независимо от интенсивности волнения (для различных волнограмм
в группе по записям ветровых волн показали, что независимо от интенсивности волнения (для различных волнограмм  изменялось от 0,2 до 4,5 м) группа в среднем состоит из 5—6 волн. Однако число волн в конкретной группе зависит от высоты наибольшей волны в ней. Чем больше высота волн, тем больше число волн в группе. Так, если в штормовом волнении высота наибольшей волны в группе
изменялось от 0,2 до 4,5 м) группа в среднем состоит из 5—6 волн. Однако число волн в конкретной группе зависит от высоты наибольшей волны в ней. Чем больше высота волн, тем больше число волн в группе. Так, если в штормовом волнении высота наибольшей волны в группе  равна среднему значению всех волн в выборке, то
равна среднему значению всех волн в выборке, то  =5, если
=5, если  , то
, то  =6 и т. д.
=6 и т. д.
Для аппроксимации функции распределения числа волн M в группе учтем, что это число ограничено снизу и не может быть меньше 2 (если две соседние группы имеют по три волны, то одна—общая для обеих групп, может принадлежать только одной группе, а другая будет содержать две волны). Усеченное нормальное распределение с параметрами  =5,
=5,  и точкой усечения
и точкой усечения  достаточно хорошо описывает натурные данные (рис. 2.14). Из рис. 2.14 следует, что группы с
достаточно хорошо описывает натурные данные (рис. 2.14). Из рис. 2.14 следует, что группы с  составляют около 10%, а группы с
составляют около 10%, а группы с  встречаются в 0,5% случаев. Однако вследствие зависимости M от
встречаются в 0,5% случаев. Однако вследствие зависимости M от  в таких группах наиболее вероятны высокие волны. Обеспеченность числа волн в группе при усеченном «слева» нормальном законе, по определению, записывается в виде:
в таких группах наиболее вероятны высокие волны. Обеспеченность числа волн в группе при усеченном «слева» нормальном законе, по определению, записывается в виде:
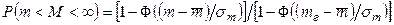 . (2.37)
. (2.37)
где  — интеграл Лапласа. Выражение (3.37) справедливо для дискретной последовательности целых т =2, 3, 4. . .
— интеграл Лапласа. Выражение (3.37) справедливо для дискретной последовательности целых т =2, 3, 4. . .

Рис. 2.14. Функция распределения числа волн в группах для штормового волнения.
1 — аппроксимация нормальным законам; 2 — натурные данные
Изучение вероятностных закономерностей, которым подчиняются сочетания волн, представляющих группы, особенно вблизи наибольшей волны в группе, представляет большой практический интерес при оценке предельных нагрузок на суда и сооружения. Помимо числа волн в группе интересно изучение высот  и периодов
и периодов  группы, которые равны соответственно вертикальному расстоянию между вершинами наибольшей и наименьшей волны в группе и временному интервалу между прохождением группы волн. Эмпирические распределения
группы, которые равны соответственно вертикальному расстоянию между вершинами наибольшей и наименьшей волны в группе и временному интервалу между прохождением группы волн. Эмпирические распределения  и
и  описываются распределением Вейбулла-Гнеденко (см. п. 1.3). Обозначая через
описываются распределением Вейбулла-Гнеденко (см. п. 1.3). Обозначая через 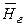 и
и  средние значения этих величин, функции распределения
средние значения этих величин, функции распределения  и
и  можно записать в виде
можно записать в виде
 ;
;  . (2.38)
. (2.38)
Элементы группы волн  и
и  —линейно зависимые случайные величины [22]. В табл. 2.2 приводятся для ветровых волн средние периоды волнения Тu,
—линейно зависимые случайные величины [22]. В табл. 2.2 приводятся для ветровых волн средние периоды волнения Тu, 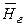 и
и  при различных средних значениях высот волнения
при различных средних значениях высот волнения  , рассчитанных по натурным данным.
, рассчитанных по натурным данным.
Таблица 2.2. Средние значения 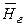 и
и  при различных
при различных  .
.
 , м , м
| 0,5 | 1,0 | 2,0 | 3,0 | 4,0 |
| Тu, с | 3,4 | 4,8 | 6,7 | 8,4 | 9,6 |
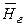 , м , м
| 0,5 | 1,0 | 2,0 | 3,0 | 4,0 |
 , с , с
|
Средние значения высот 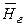 примерно равны средним значениям высот волнения
примерно равны средним значениям высот волнения  ; между средним периодом волнения Тu и их групп
; между средним периодом волнения Тu и их групп  имеется зависимость, близкая к линейной
имеется зависимость, близкая к линейной
 . (2.39)
. (2.39)
Наибольшие в группе высоты волн  являются подмножеством последовательности всех высот волн, которые распределены по закону Рэлея, поэтому распределение Р(
являются подмножеством последовательности всех высот волн, которые распределены по закону Рэлея, поэтому распределение Р(  ) должно подчиняться этому же закону, усеченному на квантили, соответствующей
) должно подчиняться этому же закону, усеченному на квантили, соответствующей  . При решении многих прикладных задач рассматриваются не все группы, а только те, в которых
. При решении многих прикладных задач рассматриваются не все группы, а только те, в которых  в
в 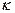 раз превышает
раз превышает  . Тогда вероятность того, что
. Тогда вероятность того, что  (обеспеченность) имеет вид распределения Рэлея, усеченного на квантили
(обеспеченность) имеет вид распределения Рэлея, усеченного на квантили 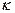
 (2.40)
(2.40)
Периоды максимальных волн в группах являются подмножеством всех периодов, определенных из условия  . Поэтому распределение периодов максимальных волн в группе должно подчиняться условному распределению периодов для различных высот. Значения параметров распределений могут быть найдены с учетом формы спектральной плотности волнения.
. Поэтому распределение периодов максимальных волн в группе должно подчиняться условному распределению периодов для различных высот. Значения параметров распределений могут быть найдены с учетом формы спектральной плотности волнения.
Результаты анализа высот и периодов волн в группе, непосредственно предшествующих волне с наибольшей высотой  и следующих
и следующих  за
за  , достаточно подробно изложены в работе [22]. Распределение величин
, достаточно подробно изложены в работе [22]. Распределение величин 
 допустимо считать нормальным. Отметим, что
допустимо считать нормальным. Отметим, что
 (2.41)
(2.41)
 (2.42)
(2.42)
 (2.43)
(2.43)
Временной интервал между прохождением групп с высотами  будем характеризовать статистикой
будем характеризовать статистикой  . Вид закона, аппроксимирующего распределение
. Вид закона, аппроксимирующего распределение  , следует из теории выбросов случайных процессов, где показано, что для больших по сравнению со временем корреляции промежутков времени
, следует из теории выбросов случайных процессов, где показано, что для больших по сравнению со временем корреляции промежутков времени  распределение экспоненциально
распределение экспоненциально
F(t) = exp(-  /
/  ). (2.44)
). (2.44)
Из рис. 2.15 следует, что чем слабее волнение, тем при заданном 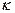 больше величина
больше величина  .
.

Рис. 2.15. Зависимость среднего временного интервала  между группами от средней высоты волн
между группами от средней высоты волн  и уровня
и уровня 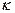 :
:
1 — 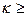 1,43 (для обеспеченности 20%); 2 —
1,43 (для обеспеченности 20%); 2 — 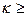 1,95 (для обеспеченности 5%); 3—
1,95 (для обеспеченности 5%); 3— 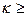 2,11 (для обеспеченности 3%); 4 — натурные данные.
2,11 (для обеспеченности 3%); 4 — натурные данные.
Рассмотренные особенности структуры группы волн, статистической изменчивости и взаимозависимости ее элементов представляют большой практический интерес. Удобство приведенных выше характеристик заключается также в том, что, зная высоту волны трехпроцентной обеспеченности (или среднюю высоту волн) и средний период волн, можно для стационарного режима волнения определить практически все приведенные выше характеристики группы волн.
Метод статистических испытаний
Наиболее простую вычислительную схему анализа вероятностных распределений выходных процессов нелинейных динамических систем имеют алгоритмы, построенные на основе метода статистических испытаний (Монте-Карло). Суть метода состоит в получении решений нелинейных уравнений (4.1), описывающих поведение динамической системы, путем их численного интегрирования по времени. Полученные таким образом данные анализируются с использованием методов математической статистики и, в результате, определяются статистические характеристики выходных процессов.
Расчет по методу Монте-Карло состоит из следующих этапов:
1. Определяется выборка u1n, u2n, ... , ukn, ... , umn случайных чисел  (входных случайных параметров), используемых в описании модели входного процесса (волнения)
(входных случайных параметров), используемых в описании модели входного процесса (волнения)  с помощью зависимостей типа (1.5), например, в виде (1.10). Каждый вариант выборки (с номером n) строится в соответствии с заданными законами распределения вероятностей входных случайных параметров.
с помощью зависимостей типа (1.5), например, в виде (1.10). Каждый вариант выборки (с номером n) строится в соответствии с заданными законами распределения вероятностей входных случайных параметров.
Для этой операции используют специальные программы для ЭВМ, датчики случайных чисел, генераторы случайных функций [83, 84, 89].
2. Каждая из N выборок входных случайных параметров определяет реализацию входного процесса X(u1n, u2n, ... , ukn, ... , umn, t). Для каждой такой реализации выполняется численное интегрирование системы уравнений (4.1) и находятся реализации установившихся выходных процессов, из которых определяются исследуемые выходные процессы Yj. В результате получаем реализации процессов Y1n, Y2n, ... , Yjn, ... , Ymn (n = 1, 2, ..., N).
3. Оцениваются статистические характеристики выходного процесса Yj (или, если это необходимо, функций от них  ); в частности, находятся следующие параметры:
); в частности, находятся следующие параметры:
- математическое ожидание
 ; (4.2)
; (4.2)
- моменты системы случайных величин
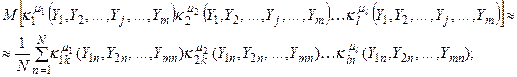 (4.3)
(4.3)
- вероятность того, что некоторая функция  будет принимать значения в пределах b1 £ x(Aj) < b2
будет принимать значения в пределах b1 £ x(Aj) < b2
 , (4.4)
, (4.4)
где М - число реализаций, при которых выполняется неравенство в формуле (4.4).
Оценки статистических характеристик случайных процессов Yj, выполняемые по формулам (4.2)-(4.4), сами являются случайными величинами.
Их изменчивость (а, следовательно, и точность оценок) существенно зависят от типа исследуемого параметра, от выбранной модели морского волнения и числа реализаций N (числа повторений численного эксперимента).
В связи со статистической изменчивостью оценок, получаемых методом Монте-Карло, важно знать, какое число реализаций N следует выбрать чтобы, например, оценка вероятности по формуле (4.4) отличалась от своего истинного значения не больше, чем на некоторую заданную величину (не выходила за доверительный интервал e) с заданной доверительной вероятностью.
Пусть истинное значение вероятности будет  . Тогда справедливы следующие приближенные выражения [89]:
. Тогда справедливы следующие приближенные выражения [89]:
- для дисперсии оценки вероятности P
 ,
,
- для потребного числа реализаций N
 . (4.5)
. (4.5)
Здесь e - требуемая точность оценки вероятности, а в качестве меры точности принято отношение среднеквадратического отклонения оценки к ее среднему значению, т.е.
 .
.
При относительно грубой оценке малых вероятностей P (например, в зоне экстремальных значений внешних сил) e можно принять равным единице. Тогда из формулы (4.5) следует, что для оценки экстремальных величин нагрузок на стационарных режимах волнения (вероятностных распределений в области малых обеспеченностей) требуемое число N построений численного (физического) эксперимента составляет величины порядка 104. Учитывая огромные затраты машинного времени на численное интегрирование уравнений типа (4.1) для получения такого числа реализаций (или затраты труда на осуществление модельного эксперимента), следует признать, что классические схемы метода Монте-Карло мало пригодны для исследования экстремальных значений нагрузок. Вместе с тем этот метод позволяет относительно малыми затратами получать моментные и некоторые другие характеристики вероятностных распределений нагрузок на конструкции высокоскоростных судов. Однако в любом случае, как это следует из формулы (4.5), увеличение числа реализаций приводит к убыванию погрешности с небольшой скоростью порядка 1/  , поэтому применение метода статистических испытаний неизбежно ведет к чрезмерным затратам машинного времени.
, поэтому применение метода статистических испытаний неизбежно ведет к чрезмерным затратам машинного времени.
Поиск более экономичных приемов решения нелинейных задач статистической динамики привел к появлению ряда других методов, родственных рассмотренному методу. Среди них наибольшую популярность имеют метод Б.Г.Доступова (метод эквивалентных возмущений) [2, 84] и интерполяционный метод В.И.Чернецкого [2, 88, 89]. В этих методах процедура получения выборок случайных чисел заменяется фиксированием их на некоторых рациональных уровнях, что делает эти методы с алгоритмической точки зрения более простыми, чем метод Монте-Карло. Однако область применения этих методов весьма ограничена.
4.3. Метод преобразования плотности распределения вероятностей
функций случайных величин
При вероятностном анализе решений такой системы, как показано в работах [2, 88, 89], целесообразно выполнять неканоническое разложение входного процесса. При таком разложении уравнение взволнованной поверхности жидкости в подвижной системе координат, связанной с движущимся со скоростью v судном, записывается в виде [36, 47]

где R - случайная величина, подчиняющаяся закону Релея с параметром, равным дисперсии  нормального процесса x(t); W - случайная величина с ПРВ pw, равной отношению спектральной плотности Sw процесса x(t) к дисперсии
нормального процесса x(t); W - случайная величина с ПРВ pw, равной отношению спектральной плотности Sw процесса x(t) к дисперсии  , g - ускорение свободного падения; j- курсовой угол движения судна по отношению к направлению распространения волн;
, g - ускорение свободного падения; j- курсовой угол движения судна по отношению к направлению распространения волн;  - случайная фаза, распределенная равномерно на промежутке [0,2p].
- случайная фаза, распределенная равномерно на промежутке [0,2p].
Случайные величины R, W и  независимы.
независимы.
При решении задач статистической динамики линейные и нелинейные системы (а также подсистемы и элементы) принято делить на инерционные и безынерционные [12-14, 69]. Если амплитуды и другие параметры выходного процесса зависят от частоты входного процесса, то такая система является инерционной. В противном случае систему можно считать безынерционной. Характерным признаком безынерционной системы является совпадение фаз возмущения (входного сигнала) и реакции системы (выходного сигнала), т.е. отсутствие задержки.
Обычно считают, что метод преобразования ПРВ функций случайных величин пригоден для исследования безынерционных систем [12, 69]. Однако представляется достаточно очевидным, что если система обладает инерционными свойствами, но входной случайный процесс реализуется на одной несущей частоте (частота фиксирована, а амплитуда обладает статистической изменчивостью, то использование рассматриваемого метода правомерно. Более того, при использовании специальных приемов, описанных ниже в параграфе 4.5, этот метод может применяться к инерционным системам, возбуждаемым входным процессом со статистически изменчивой частотой.
В данной главе излагается метод функционального преоб
Последнее изменение этой страницы: 2017-07-07
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...