Эргодическое свойство стационарных случайных функций

Для определения математического ожидания и корреляционной функции случайной функции Х(t) по данным эксперимента необходимо располагать достаточно большим числом ее реализаций. Однако в ряде случаев основные статистические свойства стационарной случайной функции могут быть определены не по множеству, а по одной достаточно длительной реализации. Другими словами, любая реализация некоторой стационарной случайной функции достаточной продолжительности является “полномочным представителем” всей совокупности реализаций этой функции. Стационарные случайные функции, для которых это положение справедливо, называются эргодичными или удовлетворяющими эргодическому свойству.

Можно показать, что достаточным условием эргодичности случайной стационарной функции (по отношению к математическому ожиданию) является условие неограниченного убывания ее корреляционной функции по модулю при (рис. 1.11). Этим свойством обладают процессы установившегося волнения и вызванные таким волнением процессы—качка, волновые моменты и др.

Рис. 1.11. Вид корреляционной функции эргодичного процесса.

Располагая достаточно длительной (за время Т) реализацией 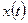случайной функции 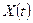можно найти математическое ожидание по формуле

(1.31)

Корреляционная функция определится зависимостью

(2.32)

Примером эргодического процесса является стационарный гауссовский процесс.

Следует отдельно обсудить вопрос об оценке экстремальных значений случайной функции по ее конечной реализации. В ряде случаев статистические свойства эргодичной стационарной случайной функции в области малых вероятностей (сопоставимых с обеспеченностью экстремальной величины на данной реализации) не могут быть определены по одной (пусть даже и относительно длительной) реализации.

Сложение случайных процессов

В приложениях часто встречаются случайные процессы, являющиеся результатом сложения нескольких случайных функций. Например, перемещения в произвольной точке судна, обусловленные стационарным случайным процессом морского волнения, представляют сумму перемещений при отдельных видах качки (вертикальной, килевой, бортовой и др.), рассматриваемых, в ряде случаев, как стационарные нормальные процессы.

Для определения характеристик суммарного, процесса необходимо знание так называемой взаимной корреляционной функции (или корреляционной функции связи).

Пусть

где a, b — неслучайные множители. Тогда математическое ожидание будет определяться по формуле

(1.33)

где т_x и т_y—математические ожидания функций X (t) и Y(t). Корреляционная функция суммарного процесса Z(t)

(1.34)

Величина называется взаимной корреляционной функцией; она равна корреляционному моменту соответствующих сечений случайных функций X(t) и Y(t)

(1.35)

Отметим, что взаимная корреляционная функция процессов X (t) и Y(t) не равна взаимной корреляционной функции Y(t)и X (t)

Если переставить местами аргументы, то взаимные корреляционные функции равны

(1.36)

В ряде случаев вводится нормированная взаимная корреляционная функция

(1.37)

где и — стандарты функций X(t) и Y(t).

Для стационарных случайных функций вместо (2.34) получим

(1.38)

Переходя к дисперсии случайного процесса Z(t), положим в (2.38)

(1.39)

Здесь R_xy(0) есть не что иное, как корреляционный момент системы случайных величин X(t) и Y(t):

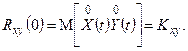
Корреляционный момент часто находят по известной взаимной спектральной плотности процессов X(t) и Y(t), которая, по определению, равна преобразованию Фурье взаимной корреляционной функции :

(1.40)

Корреляционный момент выражается через взаимную спектральную плотность так

(1.41)

Обобщая зависимость (1.39) на случай сложения большого числа случайных функций

можно получить

(1.42)

Если взаимная корреляционная функция равна нулю, то соответствующие случайные функции называются некоррелированными. В этом случае при и вместо (1.42) получим

(1.43)

Заметим здесь, что процессы, получаемые при сложении гауссовских процессов (также как и линейных действиях над ними) являются снова гауссовскими. Так, например, если компонента напряженного состояния в какой-либо точке конструкции является суммой коррелированных и центрированных гауссовских процессов, порождаемых воздействием нескольких изменяющихся во времени сил Q_j, то распределение ординат этой компоненты подчиняется нормальному закону, а для определения единственного параметра распределения суммарного процесса пригодны приведенные здесь формулы.