Весовая функция линейной системы

Рассмотрим линейную систему с n входами и m выходами. На основе принципа суперпозиции выходной сигнал на k-м выходе системы, имевшей в момент времени нулевые начальные условия, выражается при через входные сигналы формулой

(3.2)

Здесь

, (3.3)

где – весовая функция (функция Грина, импульсная переходная функция или импульсная реакция) системы по l-му входу и k-му выходу.

Функцию , представленную формулой (3.2), можно интерпретировать как изменение во времени k-й обобщенной координаты механической системы с n степенями свободы при действии на нее n приведенных (обобщенных) внешних сил . Функцию можно представить в виде реакции k-й обобщенной координаты механической системы на единичный приведенный импульс, соответствующий l-й форме колебаний системы.

Совокупность весовых функций , соответствующих всем входам и выходам, является исчерпывающей характеристикой многомерной линейной системы.

Стационарной называется такая система, у которой при любом сдвиге входного сигнала во времени без изменения его формы (т.е. при замене на 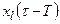при любом Т) выходной сигнал претерпевает тот же сдвиг во времени и не изменяет своей формы (т. е. заменяется на ).

Легко видеть, что система дифференциальных уравнений (3.1), стационарна тогда и только тогда, когда правые части этих уравнений, т. е. функции и не зависят явно от времени. Такое условие в задачах строительной механики корабля выполняется только при их упрощенной постановке. Как уже отмечалось, взаимодействие судна с волнами часто сопровождается большими изменениями смоченной поверхности судна и, соответственно, значительными колебаниями инерционных характеристик судна и судовых конструкций. Присоединенные массы жидкости зависят от процесса волнения и, следовательно, от времени. Явная зависимость от времени коэффициентов дифференциальных уравнений (уравнений качки и гидроупругих колебаний корпуса) и; соответственно, функции дают основание считать систему (3.1) в общем случае нестационарной.

Передаточная функция стационарной линейной системы.

Из определения стационарной системы следует, что весовая функция стационарной линейной системы зависит только от разности ее аргументов. Действительно, согласно определению реакция стационарной линейной системы в момент t на единичный импульс, действующий в момент t, совпадает с ее реакцией в момент t-t на единичный импульс, действующий в нулевой момент, т. е. при всех t, t. Положив , будем иметь .

Основной особенностью стационарных линейных систем является то, что любая устойчивая стационарная линейная система преобразует входной сигнал, представляющий собой показательную функцию е^st, без изменения его формы. На выходе системы оказываются измененными лишь ординаты сигнала прямо пропорционально некоторому множителю 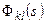, называемому коэффициентом усиления. Действительно, положив в (3.3) в случае одномерной системы , получим

где (3.4)

Эти формулы подтверждают обоснованность нашего утверждения и показывают, что коэффициент усиления показательной функции зависит от параметра s. Этот коэффициент называется передаточной функцией от входа l к выходу k стационарной линейной системы. В совокупности функции 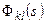образуют m´n-матрицу — передаточную функцию многомерной системы.

Высказанное утверждение о неизменяемости формы сигнала верно и для комплексного параметра s. Чтобы убедиться в этом, достаточно вспомнить, что на основании принципа суперпозиции реакция линейной системы на комплексный входной сигнал представляет собой комплексную функцию времени, действительная и мнимая части которой равны реакциям системы на действительную и мнимую части входного сигнала соответственно. Конечно, при отличной от нуля мнимой части параметра s функция 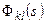имеет комплексное значение. Это означает, что стационарная линейная система сохраняет форму гармонических колебаний с амплитудой, изменяющейся по показательному закону, усиливая их амплитуду и сдвигая фазу. При этом коэффициент усиления амплитуды равен модулю передаточной функции | 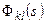|, а сдвиг фазы равен - arg .

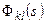Частотная характеристика стационарной линейной системы.

Рассматривая в качестве входного сигнала гармонические колебания , мы, по существу, сужаем область определения передаточной функции 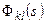, представляющую собой комплексную плоскость, до мнимой оси этой плоскости, т.е. ограничиваемся чисто мнимыми значениями параметра и получаем передаточную функцию вида . В этом случае определяет коэффициент усиления амплитуды гармонических колебаний на входе l | | и сдвиг фазы arg гармонических колебаний на выходе k по сравнению со входными как функции частоты 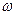. Поэтому передаточная функция системы, рассматриваемая как функция чисто мнимого параметра (т. е. суженная на мнимую ось комплексной плоскости), называется частотной характеристикой стационарной линейной системы. Коэффициент усиления амплитуды | | (модуль частотной характеристики) называется амплитудной или амплитудно-частотной характеристикой, а сдвиг фазы arg - фазовой или фазово-частотной характеристикой.

Заметим здесь, что свойство некоторых динамических систем пропускать гармонические колебания без изменения их формы, а только изменяя амплитуду и сдвигая фазу, дающее возможность исследовать их алгебраическими методами и методами функционального преобразования случайных величин, лежит в основе метода исследования динамических систем в частотной области, который используется применительно не только к линейным системам, но и к слабо нелинейным.

С помощью частотной характеристики устойчивой линейной системы легко вычисляется ее установившаяся реакция на любой входной сигнал, который можно разложить на элементарные гармонические колебания (т. е. представить рядом или интегралом Фурье).

Предположим, что центрированный входной сигнал X устойчивой стационарной линейной системы может быть представлен интегралом Фурье (см. формулу (1.16) )

(3.5)

Тогда на основании принципа суперпозиции установившийся выходной сигнал Y (при бесконечно долгом действии входного сигнала X) определится формулой

(3.6)

В частности, представив функцию интегралом Фурье [77, приложение 1]

выразим реакцию системы на импульсный входной сигнал , т.е. ее весовую функцию, через частотную характеристику

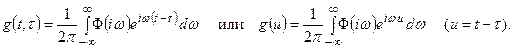
Таким образом, весовая функция и частотная характеристика стационарной линейной системы связаны между собой преобразованием Фурье. Следовательно,

Так как любой ограниченный непрерывный входной сигнал, действующий на конечном интервале времени (а только такие сигналы приходится рассматривать в задачах практики), можно представить интегралом Фурье, то с помощью частотных характеристик можно вычислять установившиеся выходные сигналы устойчивых стационарных линейных систем практически при любых входных сигналах.

4.3. Преобразование стационарной случайной функции стационарной линейной динамической системой. Спектральная плотность и дисперсия выходного процесса

На практике системы, обладающие строго выраженной линейностью, встречаются крайне редко. Как правило, нелинейность проявляется наиболее отчетливо в тех случаях, когда исследуются статистики экстремальных значений процессов. Однако если изучаемая система не является сильно нелинейной, то описываемые здесь методы исследования линейных систем приведут к осмысленным результатам, представляющим собой линейные приближения к реальным процессам.

Примерами выходных процессов, которые часто подвергаются приближенному анализу с помощью линейных математических моделей, могут служить процессы качки водоизмещающих судов, волнового давления на днище, волновых моментов в сечениях корпуса этих судов и т. п.

Если динамическая система линейна и стационарна, а входные процессы стационарны, то и выходные процессы будут стационарными. Для стационарных процессов задача преобразования может быть сведена к преобразованию лишь одной неслучайной функции — спектральной плотности.

Рассмотрим линейную стационарную систему с одним входом и m выходами. Выходной сигнал м на k-выходе системы отыщем следующим образом (см. формулу (3.6)

(3.7)

Здесь - частотная характеристика k-го выхода; - случайная функция с корреляционной функцией 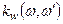, определяемой формулой (1.17), т.е. равной .

Взаимная корреляционная функция сигналов и на k-м и j-м выходах равна

Подставляя сюда функцию 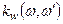, определяемую формулой (1.17), и интегрируя по переменной , получим

(3.8)

Обозначив произведение первых трех сомножителей в подынтегральном выражении через

, (3.9)

получим

(3.10)

Отсюда следует, что преобразованием Фурье функции является взаимная корреляционная функция . Следовательно, представляет собой взаимную спектральную плотность процессов (см. формулу (1.40) ).

Таким образом, при преобразовании стационарных СП стационарной линейной системой взаимная спектральная плотность выходных процессов равна спектральной плотности входного процесса, умноженной последовательно на частотную характеристику выхода k системы и на сопряженную частотную характеристику выхода j.

При совпадении индексов (при k = j) рассматривается единственный процесс и формулы (3.8) и (3.9) дают соответственно значения корреляционной функции и спектральной плотности для одного процесса (т.е значения автокорреляционной функции и автоспектра)

; (3.11)

. (3.12)

Следовательно, при преобразовании стационарного СП стационарной линейной системой каждая из ординат автоспектра определяется как произведение спектральной плотности волнения на квадрат модуля частотной характеристики (на квадрат амплитудной характеристики) для соответствующей частоты.

 

4.4. Преобразование стационарной случайной функции линейной дифференциальной системой

 

1. Система, описываемая дифференциальным уравнением с постоянными коэффициентами

 

В этом случае вероятностные характеристики решений дифференциального уравнения при стационарных возмущениях получаются весьма просто. Возможны два вида решений уравнения - нестационарные и стационарные. При действии стационарного случайного возмущения устойчивое нестационарное решение уравнения с постоянными коэффициентами, может иметь место, только в самом начале стационарного режима. Такая ситуация реализуется при наличии нестационарностей, обусловленных переходом с одного режима возмущения на другой, например, когда система начинает двигаться из состояния покоя под действием стационарного возмущения. Если дифференциальная система асимптотически устойчива, то нестационарные случайные колебания обычно быстро затухают и после небольшого промежутка времени с ними можно не считаться. Кроме того, при обычных (неаварийных) эксплуатационных условиях переходы от одного стационарного режима эксплуатации судна к другому осуществляются постепенно, плавно и поэтому не сопровождаются ярко выраженными нестационарными явлениями. В связи с этим для решения большинства проблем прочности и надежности судовых конструкций наибольший интерес представляют стационарные решения и стационарные режимы колебаний судна и его конструкций.

Стационарные случайные колебания имеют место в устойчивых системах, в которых возможны установившиеся колебания при действии периодических возмущений. Удобный аппарат анализа стационарных решений линейных уравнений с постоянными коэффициентами дает операционное исчисление. Напомним его основные положения.

Преобразование Лапласа некоторой функции независимой вещественной переменной t определяется соотношением

где s — некоторая комплексная переменная. Функцию называют оригиналом, а функцию — изображением. В таблице 4.1 приведены приведены некоторые оригиналы и их изображения, дающие представление о правилах нахождения функций и .

 

Таблица 3.1. Типовые функции и их изображения.

 

Рассмотрим дифференциальное уравнение порядка n с постоянными коэффициентами

. (3.13)

Применим преобразование Лапласа к этому уравнению. Воспользовавшись таблицей оригиналов типовых функций и полагая начальные условия нулевыми ( ), можно привести уравнение (3.13) к виду

, (3.14)

где и — изображения функций и . Из равенства (4.14) получаем

(3.15)

Функция в уравнении (3.15) представляет собой отношение изображений выходного и входного сигналов (при нулевых начальных условиях) и имеет тот же смысл, что и функция (3.4), выраженная как преобразование Лапласа функции Грина системы. Она называется передаточной функцией системы. Как отмечалось ранее, частотная характеристика находится путем замены аргумента s в операторе на . Спектральная плотность выходного процесса связана со спектральной плотностью входного процесса и модулем частотной характеристики выражением, аналогичным (3.12)

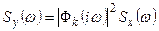. (3.16)

 

2. Система, описываемая линейными дифференциальными уравнениями с периодическими коэффициентами

 

При решении задач гидроупругости судовых конструкций приходится сталкиваться с периодическим изменением присоединенных масс жидкости, обусловленным изменением смоченной поверхности судна при взаимодействии его с волнами. В частности, такая проблема возникает при анализе волновой вибрации судов [33]. В дифференциальных уравнениях, описывающих качку судов, переменными во времени могут быть не только инерционные коэффициенты, но и коэффициенты демпфирующих и восстанавливающих сил. Рассмотрим движение системы с одной степенью свободы с переменными коэффициентами , зависящими от времени (такая система анализируется при изучении волновой вибрации)

, (3.17)

где - случайный процесс.

Полагая , представим уравнение (3.17) в виде системы двух уравнений первого порядка

или одного векторного уравнения

, (3.18)

где

.

Общее решение уравнения (3.18) можно представить в виде

, (3.19)

где - фундаментальная матрица решений (матрицант) однородного уравнения (3.18), равная при t=0 единичной матрице; - вектор начальных данных; - матрица Грина.

Компоненты вектора могут быть представлены как детерминированными, так и случайными величинами. Будем полагать, что вероятностные характеристики (математические ожидания и дисперсии ) этих компонент известны. Математическое ожидание вектора

;

или в скалярном виде

Автокорреляционная функция и дисперсия процесса

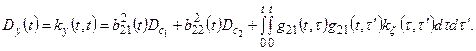
Решение уравнения (3.17) отыскиваем в виде ряда по степеням малого параметра

. (3.20)

Предполагая, что решение (3.20) удовлетворяет уравнению (3.17) тождественно по и поэтому коэффициент при каждой степени должен обратиться в нуль, получаем следующую систему уравнений:

;

;

Таким образом

;

;

 

 

, (27-1)

или

(27-2)

 

Рассмотрим движение системы с одной степенью свободы с переменными инерционными коэффициентами, зависящими от процесса волнения (такая система анализируется при изучении волновой вибрации)

, (4.13)

где M – постоянная составляющая приведенной массы судна и присоединенной воды; - малый постоянный параметр; k_m – постоянный коэффициент; N и C – приведенные коэффициенты демпфирования и жесткости соответственно; - случайный процесс волнения.

Решение уравнения (4.13) отыскиваем в виде ряда по степеням малого параметра

. (4.14)

Предполагая, что решение (4.14) удовлетворяет уравнению (4.13) тождественно по и поэтому коэффициент при каждой степени должен обратиться в нуль, получаем следующую систему уравнений:

;

;

 

 

, (27-1)

или

(27-2)