Категории:
ДомЗдоровьеЗоологияИнформатикаИскусствоИскусствоКомпьютерыКулинарияМаркетингМатематикаМедицинаМенеджментОбразованиеПедагогикаПитомцыПрограммированиеПроизводствоПромышленностьПсихологияРазноеРелигияСоциологияСпортСтатистикаТранспортФизикаФилософияФинансыХимияХоббиЭкологияЭкономикаЭлектроника
Глава 1. Дифференциальные уравнения в частных производных, их классификация и методы решения. Задача Коши
Предисловие
В настоящем пособии рассматриваются некоторые виды уравнений в частных производных и методы их решения.
Дифференциальные уравнения в частных производных, которые встречаются при решении физических задач, называют также уравнениями математической физики. К ним относятся волновое уравнение, уравнение теплопроводности и уравнение теплового состояния (уравнения Лапласа и Пуассона). Они впервые появились почти одновременно в работах Даниила Бернулли (1700 – 1782), Жана Лерона Даламбера (1717 – 1783) и Леонарда Эйлера (1707 – 1783), позднее - в работах Жана Батиста Фурье (1768 – 1830). Бернулли получил решение волнового уравнения в виде тригонометрического ряда, Даламбер и Эйлер представили решение в виде прямой и обратной волн, что и дало название уравнению. Фурье показал эквивалентность этих двух решений.
Нахождение точного аналитического решения дифференциальных уравнений в частных производных, к сожалению, возможно лишь для весьма ограниченного круга одномерных задач при использовании целого ряда допущений, негативно отражающихся на адекватности полученных результатов. Для решения задач математической физики в случае нескольких измерений необходимо использовать численные методы, позволяющие преобразовывать дифференциальные уравнения или их системы в системы алгебраических уравнений. Для решения полученных нелинейных систем алгебраических уравнений или линейных систем большой размерности используют итерационные методы. При этом одной из наиболее сложных проблем является обеспечение сходимости итерационного процесса, в значительной степени, определяющей время вычислений. Точность решения определяется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера. Рассмотренные методы решения уравнений в частных производных проиллюстрированы примерами для системы MATLAB.
Пособие содержит три главы. В главе 1 рассматриваются уравнения в частных производных, общее решение которых можно найти с помощью повторного интегрирования. Вводится понятие задачи Коши для уравнений 1-го и 2-го порядков и классификация уравнений 2-го порядка в частных производных. Представлены численные методы решения параболических, гиперболических и эллиптических дифференциальных уравнений с использованием пакета MATLAB.
В главе 2 представлены классические методы решения уравнения свободных колебаний струны: метод Даламбера для бесконечной струны, метод продолжений для полубесконечной и конечной струны, а также метод Фурье (метод разделения переменных) для конечной струны, закрепленной на концах.
В главе 3 рассматривается метод Фурье для уравнения распространения тепла в однородном стержне и уравнения Лапласа в случае некоторых простейших областей (круг, кольцо, прямоугольник).
Теоретический материал проиллюстрирован примерами, в которых используется статичная и анимационная графика, выполненная в среде MATLAB.
Кроме того, в пособии приведены лабораторные работы, посвященные численным методам решения задачи Коши и уравнений математической физики с использованием пакета MATLAB.
Глава 1. Дифференциальные уравнения в частных производных, их классификация и методы решения. Задача Коши
Упражнения.
Найти общее решение 
следующих дифференциальных уравнений с частными производными. Выполнить проверку.
1.1. 
.
Ответ: 
.
1.2. 
.
Ответ: 
.
1.3. 
.
Ответ: 
.
1.4. 
.
Ответ: 
.
1.5.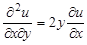 
.
Ответ: 
.
1.6. 
.
Ответ: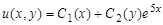 
.
1.7.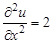 
.
Ответ: 
.
1.8. 
.
Ответ: 
.
1.9. 
.
Ответ: 
.
1.10. 
.
Ответ: 
.
1.11. 
.
Ответ: 
.
1.12. 
.
Ответ: 
.
Начальные и граничные условия
1.2.1. Задача Коши для дифференциальных уравнений первого порядка
Будем рассматривать случай, когда искомая функция 
зависит от двух переменных 
. Тогда уравнение 1-го порядка будет иметь вид
.
Всякое решение данного уравнения будем называть интегральной поверхностью (график решения – поверхность в пространстве с координатами 
).
Для того чтобы из совокупности всех решений данного уравнения выделить некоторое частное решение, формулируется задача Коши: найти решение уравнения , удовлетворяющее условию 
, где 
– некоторая заданная функция.
Обозначим через l кривую в пространстве , задаваемую уравнениями: 
.
Тогда задача Коши имеет следующий геометрический смысл: среди всех интегральных поверхностей найти ту, которая проходит через заданную кривую l.
1.2.2. Задача Коши для дифференциальных уравнений второго порядка
Дифференциальные уравнения с частными производными, вообще говоря, имеют бесчисленное множество решений. Для того чтобы из этого множества выбрать то единственное решение, которое соответствует реальному физическому процессу (например, колебанию данной струны), надо задать некоторые дополнительные условия. В теории уравнений с частными производными, как и в обыкновенных дифференциальных уравнениях, задаются условия, называемые начальными и краевыми (граничными) условиями. Начальные условия в математической физике соответствуют состоянию физического процесса в начальный момент времени, который обычно принимают за 
. В результате возникает задача Коши:
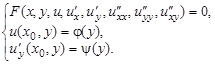
Однако здесь есть некоторые отличия. Во-первых, начальные условия задаются для нестационарных уравнений, т.е. уравнений, описывающих нестационарные (зависящие от времени) процессы. Такими уравнениями являются, к примеру, волновые уравнения и уравнения теплопроводности. Во-вторых, задача Коши для уравнений с частными производными имеет единственное решение только в том случае, когда соответствующее уравнение рассматривается или на всей прямой, или на всей плоскости, или во всем пространстве. Например, это может быть задача о колебании бесконечной струны или о распространении тепла в бесконечном стержне. На практике к таким задачам приходят в том случае, когда имеется очень длинная струна или очень длинный стержень и интересуются процессами, происходящими далеко от концов, а влиянием концов пренебрегают. Если взять, допустим, длинный провод и слегка качнуть его в середине, то по нему влево и вправо побегут волны. Картина начнет искажаться только тогда, когда волны дойдут до концов провода и, отразившись, пойдут обратно. Следовательно, не учитывая влияния концов, мы тем самым не будем учитывать влияния отраженных волн.
Для волнового уравнения 
задаются два начальных условия: 
и 
. Первое условие физически задает начальную форму струны (начальные отклонения точек струны), а второе условие – начальные скорости точек струны. В случае волнового уравнения на плоскости или в пространстве задаются те же два начальных условия, только функции φ и ψ, соответственно, будут зависеть от двух или трех переменных.
Если размеры струны или стержня не очень велики и влиянием концов нельзя пренебречь, то в этих случаях одни начальные условия уже не обеспечивают единственность решения задачи. Тогда необходимо задавать условия на концах. Они называются граничными или краевыми условиями. Если в задаче заданы начальные и граничные условия, то такая задача называется смешанной.
Для уравнения колебаний струны часто задаются условия: 
. Эти условия физически означают, что концы струны закреплены (т.е. отклонения при 
и при 
в любой момент времени равны нулю). Можно задавать и другие условия на концах струны, например, 
– свободные концы струны.
Упражнения.
1.13. К какому типу относится уравнение колебания струны 
?
Ответ: гиперболическому.
1.14. К какому типу относится уравнение теплопроводности 
?
Ответ: параболическому.
1.15. К какому типу относится уравнение Лапласа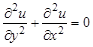 
?
Ответ: эллиптическому.
Жесткое закрепление.
Рассмотрим случай, когда струна жестко закреплена в точке , т.е. в данной точке отклонение струны всегда равно нулю.
Задача ставится следующим образом: ищем решение системы уравнений
Рассмотрим функци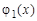и 
и 
(x), являющиеся нечетными продолжениями функций 
и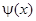 
. Тогда функция
определена для всех 
. В силу леммы 1 
.
Кроме того, эта функция удовлетворяет при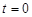 
и 
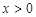следующим начальным условиям:
Таким образом, рассматривая полученную функцию 
только для 
, мы получим функцию, удовлетворяющую всем условиям поставленной задачи.
Свободное закрепление.
Теперь рассмотрим случай, когда при 
мы имеем свободный конец. Это значит, что касательная в точке 0 параллельна оси x:
Делаем четное продолжение функци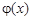й 
и 
. Получим решение уравнения колебаний в виде функции
,
определенной для всех . В силу леммы 2 
.
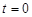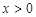Кроме того, эта функция удовлетворяет при и следующим начальным условиям:
Таким образом, рассматривая полученную функцию только для , мы получим функцию, удовлетворяющую всем условиям поставленной задачи.
Вывод.Для решения задачи на полуограниченной прямой с граничным условием начальные данные надо продолжить на всю прямую нечетным образом.
Для решения задачи на полуограниченной прямой с граничным условием начальные данные надо продолжить на всю прямую четным образом.
2.2.4. Метод продолжения для конечной струны (начальная и конечная точки жестко закреплены)
Рассмотрим краевую задачу для ограниченного отрезка (0, l). Будем искать решение уравнения
,
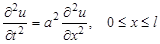удовлетворяющее граничным условиям
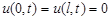
и начальным условиям
Будем искать решение задачи методом продолжения, предполагая возможность следующего представления:
,
где 
(x) и (x) – функции, подлежащие определению. Начальные условия
определяют значения 
(x) и 
(x) в интервале (0, l).
Для того чтобы удовлетворить нулевым граничным условиям, наложим на функции (x) и (x) требования нечетности относительно точек x = 0, x = l:
Сопоставляя эти равенства, получим:
и аналогично для Ψ(x), т.е. 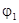(x) и (x) – периодические функции с периодом 2l.
Нетрудно видеть, что условия нечетности относительно начала координат и условия периодичности определяют продолжение 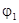(x) и 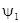(x) на всей прямой 
. Подставляя их, получаем решение задачи.
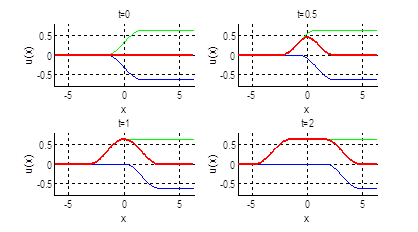
Пример. Решить уравнение колебания полубесконечной струны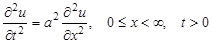 
, удовлетворяющее условиям:
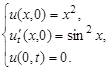
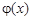Решение. Имеем задачу свободных колебаний полубесконечной струны (с краевым условием ). Так как , то продолжим функции и на отрицательную полуось нечетным образом
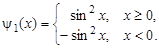
Тогда по формуле Даламбера:
=
Пример. Решить уравнение колебания полубесконечной струны 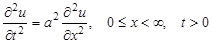, удовлетворяющее условиям:
Решение. Имеем задачу свободных колебаний полубесконечной струны (с краевым условием ). Так как , то продолжим функцию на отрицательную полуось четным образом ( 
):
, 
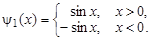
Тогда по формуле Даламбера:
= 
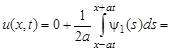
Упражнения.
Решить уравнение колебания бесконечной струны, удовлетворяющее условиям:
2.1.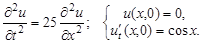 
Ответ: 
.
2.2. 
Ответ: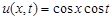 
.
2.3. 
Ответ: 
.
2.4.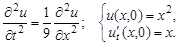 
Ответ: 
.
2.5. 
Ответ: 
.
2.6. 
Ответ: 
.
2.7. 
Ответ: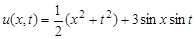 
.
2.8.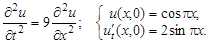 
Ответ: 
.
Решить уравнение колебания полубесконечной струны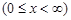 
, удовлетворяющее условиям:
2.9.
Ответ: 
2.10. 
Ответ: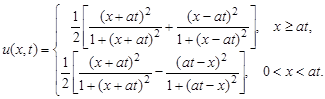 
2.11.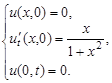 
Ответ: 
.
2.12. 
Ответ: 
2.13.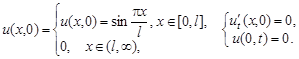 
Ответ:
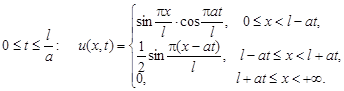
Решить уравнение колебания бесконечной струны, удовлетворяющее условиям:
2.14. 
Нарисовать профиль струны для моментов времени 
Ответ:
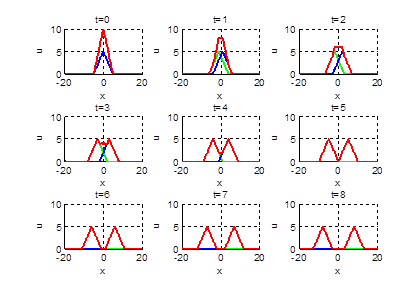
2.15.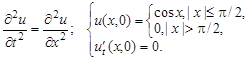 
Нарисовать профиль струны для моментов времени 
Ответ:
2.16. 
Нарисовать профиль струны для моментов времени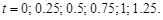 
Ответ:
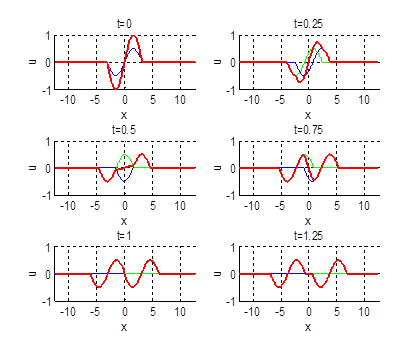
2.17. 
Нарисовать профиль струны для моментов времени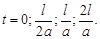 
Ответ:
2.18. 
Нарисовать профиль струны для моментов времени 
Ответ:
2.19. 
Нарисовать профиль струны для моментов времени 
Ответ:
2.3. Метод Фурье (метод стоячих волн) или метод разделения переменных
Метод Фурье или метод разделения переменных является одним из наиболее распространенных методов решения уравнений с частными производными. Суть этого метода мы продемонстрируем на примере задачи о колебаниях струны, закрепленной на концах. Итак, будем искать решение волнового уравнения с начальными и граничными условиями:
Уравнение линейно и однородно, поэтому сумма частных решений также является решением этого уравнения. Имея достаточно большое число частных решений, можно попытаться с помощью суммирования их с некоторыми коэффициентами найти искомое решение. Частные решения будем искать в виде:
где X (x) – функция только переменного x; T (t) – функция только переменного t.
Подставляя предполагаемую форму решения в уравнение, получим:
или, после деления на множитель 
,
.
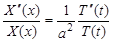Правая часть этого равенства является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение:
,
где 
– постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке. Получаем обыкновенные дифференциальные уравнения для определения функций 
и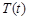 
:
Очевидно, что нас интересуют нетривиальные решения.
Граничные условия дают:
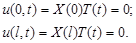
Отсюда следует
.
Таким образом, приходим к простейшей задаче: найти те значения параметра , при которых существуют нетривиальные решения задач:
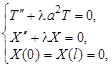
а также найти эти решения. Такие значения параметра называются собственными значениями, а соответствующие им нетривиальные решения – собственными функциями задачи. Сформулированную таким образом задачу часто называют задачей Штурма – Лиувилля.
Рассмотрим отдельно случаи, когда параметр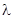 
отрицателен, равен нулю или положителен.
1. При 
задача не имеет нетривиальных решений. Действительно, общее решение уравнения 
имеет вид
,
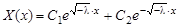Граничные условия дают:
; 
.
Отсюда 
и, следовательно,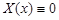 
.
2. При 
также не существует нетривиальных решений. Действительно, в этом случае общее решение уравнения имеет вид
.
Граничные условия дают:
; 
.
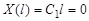Отсюда и, следовательно, .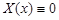
3. При 
общее решение уравнения может быть записано в виде
.
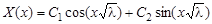Граничные условия дают:
; 
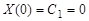Нетривиальное решение получаем только в случае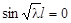 
или 
. Отсюда
.
Этим собственным значениям соответствуют собственные функции
,
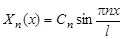где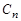 
– произвольная постоянная.
Пусть 
, тогда собственными функциями являются
.
Аналогично решаем уравнение относительно :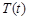
,
где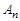 
и 
– произвольные постоянные.
Следовательно, функции
являются частными решениями данного уравнения. В силу линейности и однородности уравнения сумма частных решений также удовлетворяет этому уравнению и граничным условиям. Получаем общее решение:
.
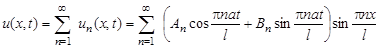Начальные условия позволяют определить 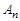и :
;
.
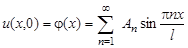Из теории рядов Фурье известно, что коэффициенты разложения в ряд Фурье вычисляются по формулам:
; 
.
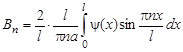Подставив эти коэффициенты в общее решение, мы удовлетворим краевым условиям и получим решение уравнения.
Простейшие задачи Штурма – Лиувилля для уравнения 
.
| Вид условия | Собственные значения и функции для 
|
|
| 
|
| 
|
| 
|
| 
|
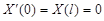
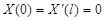
Пример. Решить уравнение колебания ограниченной струны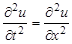 
, удовлетворяющее условиям: 
Решение. Общее решение имеет вид
.
Из начальных условий определим и :
Тогда 
.
.
Отсюда 
.
Подставив эти коэффициенты в общее решение, получим решение уравнения:
.
Можно построить в среде MATLAB поверхность 
решения данного волнового уравнения (рис.2.6).
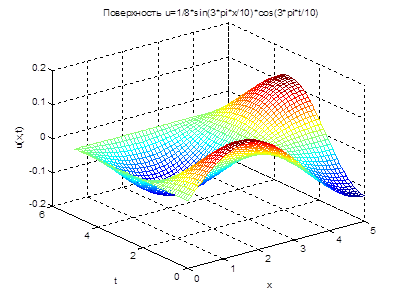
Рис.2.6. Поверхность решения уравнения колебания ограниченной струны
[x,t]=meshgrid(0:.1:5);
u=1/8*sin(3*pi*x/10).*cos(3*pi*t/10);
mesh(x,t,u)
xlabel('x')
ylabel('t')
zlabel('u(x,t)')
title('u=1/8*sin(3*pi*x/10)*cos(3*pi*t/10)')
Для лучшей визуализации напишем m-файл, который с частотой в 1 с будет демонстрировать графики решения рассмотренного ранее волнового уравнения для различных моментов времени t (рис.2.7):
figure,axis([0 10 -0.15 0.15]),grid
hold on
x=0:.1:10;
t=0:.4:2;
color=rand(3,length(t));%случайный выбор цветов волн
for k=1:length(t)
u=1/8*sin(3*pi*x/10)*cos(3*pi*t(k)/10);
plot(x,u,'LineWidth',2,'Color',color(:,k))
xlabel('x')
ylabel('u(x)')
title('Поверхность u=1/8*sin(3*pi*x/10)*cos(3*pi*t(k)/10)')
legend('t=0','t=0.4','t=0.8','t=1.2','t=1.6','t=2')
pause(1)
end
Рис.2.7. График профиля колебания ограниченной струны для различных моментов времени t
Построим анимацию в среде MATLAB колебаний конечной закрепленной на концах струны при начальных условиях, заданных в предыдущем примере:
x=0:.1:10;
for t=0:20;
u=1/8*sin(3*pi*x/10).*cos(3*pi*t/10);
plot(x,u,'r','LineWidth',2);
hold all;
xlim([0 10]);
ylim([-1/8 1/8]);
grid on;
xlabel('x');ylabel('u(x)');
M(t+1)=getframe;
pause(.2)
hold off;
end
movie(M,3)%повторяем 3 раза
Пример.Решить уравнение колебания ограниченной струны:
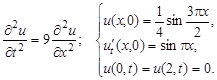
Решение. Имеем задачу свободных колебаний струны, закрепленной на концах (в точках 0 и 2). Здесь 
, т.е. 
, 
. Поэтому решение ищем в виде:
.
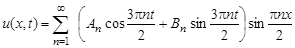Подставим t = 0:
.
Используя первое начальное условие, получаем:
.
Можно подобрать коэффициенты An так, чтобы равенство выполнялось тождественно: 
при 
, следовательно, 
.
Чтобы использовать второе начальное условие, продифференцируем u(x, t) по t:
и подставим t = 0:
.
Таким образом, получаем условие
и подбираем коэффициенты:
при 
.
Итак, имеется всего два ненулевых слагаемых:
при 
.
Окончательно, получаем решение:
Замечание.Часто начальная скорость точек струны y(х) = 0 (т.е. рассматриваются колебания струны, которую в начальный момент времени оттянули и отпустили без рывка), тогда, очевидно, Вn = 0.
Пример.Решить уравнение колебания ограниченной струны:
Решение: Имеем задачу свободных колебаний струны, закрепленной на концах ( 
, 
). Поэтому решение ищем в виде:
.
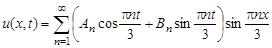Используем первое начальное условие:
.
Подобрать коэффициенты An здесь нельзя, будем их вычислять как коэффициенты Фурье разложения функции 
на интервале (0, 3) по синусам:
Второе начальное условие тривиально, поэтому Bn = 0.
Таким образом,
.
Заметим, что при 
, тогда
.
Упражнения.
Решить уравнение колебания ограниченной струны:
2.20. 
Ответ: 
.
2.21. 
Ответ: 
.
2.22. 
Ответ: 
.
2.23. 
Ответ: 
.
2.24. 
Ответ: 
.
2.25. 
Ответ: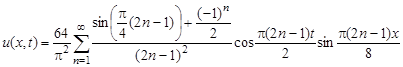 
.
2.26. 
Ответ: 
.
Упражнения.
Решить уравнение теплопроводности при заданных начальных и граничных условиях:
3.1. 
Ответ: 
.
3.2. 
Ответ: 
.
3.3. 
Ответ: 
.
3.4. 
Ответ: 
.
3.5. 
Ответ:
.
3.3. Уравнение Лапласа
При исследовании стационарных процессов различной физической природы (колебания, теплопроводность, диффузия и др.) обычно приходят к уравнениям эллиптического типа. Наиболее распространенным уравнением этого типа является уравнение Лапласа
.
Функция u называется гармоническойв области Г, если она непрерывна в этой области вместе со своими производными до 2-го порядка и удовлетворяет уравнению Лапласа.
При изучении свойств гармонических функций были разработаны различные математические методы, оказавшиеся плодотворными и в применении к уравнениям гиперболического и параболического типов. Мы будем искать решение краевых задач для простейших областей методом разделения переменных. Решение краевых задач для уравнения Лапласа может быть найдено методом разделения переменных в случае некоторых простейших областей (круг, прямоугольник, шар, цилиндр и др.). Рассмотрим некоторые из них.
3.3.1. Задача Дирихле для уравнения Лапласа в круге
Найти функцию u, удовлетворяющую уравнению Лапласа внутри круга и граничному условию 
на границе круга, где 
– заданная функция, 
– полярный угол.
Введем полярную систему координат 
с началом в центре круга:
Уравнение Лапласа в полярных координатах имеет вид
.
Решим уравнение методом разделения переменных, т.е. будем искать частное решение уравнения в виде
.
Подставляя предполагаемую форму решения в уравнение в полярных координатах, получим:
.
Отсюда
.
Получим два обыкновенных дифференциальных уравнения:
Определим знак .
1. Пусть 
, например, 
.
Рассмотрим уравнение
.
Характеристическое уравнение имеет вид
– это решение не подходит, так как при изменении угла 
на величину 
однозначная функция 
должна вернуться к исходному значению 
(условие периодичности).
Отсюда следует, что 
, т.е. 
является периодической функцией угла 
с периодом .
2. Пусть , тогда 
.
– это решение подходит
Последнее изменение этой страницы: 2017-07-07
lectmania.ru. Все права принадлежат авторам данных материалов. В случае нарушения авторского права напишите нам сюда...