Глава 3. Уравнения теплопроводности и Лапласа

Вывод уравнения теплопроводности

Рассмотрим однородный теплоизолированный с боков стержень конечной длины l имеющий постоянную по длине толщину, и настолько тонкий, чтобы в любой момент времени температуру тела во всех точках поперечного сечения можно было бы считать одинаковой.

Выберем ось х (направив ее по оси стержня) так, чтобы стержень совпадал с отрезком 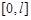оси х.

Обозначим температуру стержня в сечении х в момент времени t через . Тогда функция описывает распределения температуры в стержне. Выведем дифференциальное уравнение для этой функции.

Выделим элемент стержня и составим для него уравнение теплового баланса, согласно которому скорость изменения количества тепла в рассматриваемом объеме, обусловленная теплоемкостью материала, равна количеству тепла, поступившему в этот объем в единицу времени вследствие теплопроводности. Скорость изменения тепла в выделенном элементе стержня равна

,

где – теплоемкость материала стержня; – плотность материала; – площадь поперечного сечения. По теореме о среднем:

.

Теперь найдем количество тепла, поступившее в выделенный элемент стержня за единицу времени. Так как стержень теплоизолирован с боков, то тепло может поступать только через сечения, ограничивающие выделенный элемент стержня. Поэтому искомое количество тепла с учетом формулы Лагранжа равно:

,

где - коэффициент теплопроводности.

Составим уравнение теплового баланса

.

Разделим обе части этого уравнения на (объем выделенного элемента стержня) и устремим (тогда ). Получим

.

Это уравнение называется уравнением теплопроводности для однородного стержня. Величина называется коэффициентом температуропроводности.

Метод Фурье для конечного стержня

Уравнение теплопроводности относится к уравнениям параболического типа.

Будем искать решение уравнения теплопроводности с начальными и граничными условиями:

Частные решения данного уравнения будем искать в виде:

где X (x) – функция только переменного x; T (t) – функция только переменного t.

Подставляя предполагаемую форму решения в уравнение, получим:

или, после деления на ,

.

Правая часть этого равенства является функцией только переменного t, а левая – только х. Фиксируя, например, некоторое значение х и меняя t (или наоборот), получим, что правая и левая части равенства при изменении своих аргументов сохраняют постоянное значение

,

где – постоянная, которую для удобства последующих выкладок берем со знаком минус, ничего не предполагая при этом о ее знаке. Получаем обыкновенные дифференциальные уравнения для определения функций и :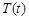

Очевидно, что нас интересуют нетривиальные решения ( ).

Граничные условия дают:

Отсюда следует

.

Таким образом, мы приходим к простейшей задаче: найти те значения параметра , при которых существуют нетривиальные решения задач

а также найти эти решения.

При решении уравнения колебания струны было доказано, что при и уравнение имеет только тривиальные решения, поэтому рассмотрим только случай . Тогда решение уравнения с учетом граничных условий имеет вид

,

а решение уравнения имеет вид

,

где 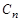– неопределенный пока коэффициент.

Тогда частные решения уравнения теплопроводности

,

а общее решение

.

Начальные условия позволяют определить :

Для выполнения этого начального условия необходимо взять в качестве 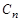коэффициент Фурье:

.

Для получения ответа необходимо подставить указанный коэффициент в общее решение задачи.

Пример.Найти решение уравнения теплопроводности при граничных условиях 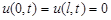и начальном условии

Решение. Общее решение уравнения имеет вид

,

где .

Вычисляя данные интегралы, получим:

; .

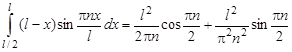Итак, . Так как , то .

Решение имеет вид

.

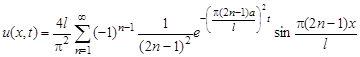Упражнения.

Решить уравнение теплопроводности при заданных начальных и граничных условиях:

3.1.

Ответ: .

3.2.

Ответ: .

3.3.

Ответ: .

3.4.

Ответ: .

3.5.

Ответ:

.

3.3. Уравнение Лапласа

При исследовании стационарных процессов различной физической природы (колебания, теплопроводность, диффузия и др.) обычно приходят к уравнениям эллиптического типа. Наиболее распространенным уравнением этого типа является уравнение Лапласа

.

Функция u называется гармоническойв области Г, если она непрерывна в этой области вместе со своими производными до 2-го порядка и удовлетворяет уравнению Лапласа.

При изучении свойств гармонических функций были разработаны различные математические методы, оказавшиеся плодотворными и в применении к уравнениям гиперболического и параболического типов. Мы будем искать решение краевых задач для простейших областей методом разделения переменных. Решение краевых задач для уравнения Лапласа может быть найдено методом разделения переменных в случае некоторых простейших областей (круг, прямоугольник, шар, цилиндр и др.). Рассмотрим некоторые из них.

3.3.1. Задача Дирихле для уравнения Лапласа в круге

Найти функцию u, удовлетворяющую уравнению Лапласа внутри круга и граничному условию на границе круга, где – заданная функция, – полярный угол.

Введем полярную систему координат с началом в центре круга:

Уравнение Лапласа в полярных координатах имеет вид

.

Решим уравнение методом разделения переменных, т.е. будем искать частное решение уравнения в виде

.

Подставляя предполагаемую форму решения в уравнение в полярных координатах, получим:

.

Отсюда

.

Получим два обыкновенных дифференциальных уравнения:

Определим знак .

1. Пусть , например, .
Рассмотрим уравнение

.

Характеристическое уравнение имеет вид

– это решение не подходит, так как при изменении угла на величину однозначная функция должна вернуться к исходному значению (условие периодичности).

Отсюда следует, что , т.е. является периодической функцией угла с периодом .

2. Пусть , тогда .

– это решение подходит при условии .

Рассмотрим второе уравнение системы:

.

Пусть

,

тогда

.

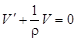Получаем: – решение уравнения в общем случае.

3. Пусть , например, . Тогда решение уравнения :

.

Рассмотрим второе уравнение системы

.

Функцию будем искать в виде . Тогда уравнение принимает вид

;

;

;

.

Следовательно, – решение уравнения, где С и D – постоянные.

Для решения внутренней задачи надо положить , так как, если , то функция обращается в бесконечность при и не является гармонической функцией внутри круга. Итак, частные решения нашей задачи найдены:

.

Вид общего решения

.

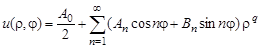Удовлетворим краевому условию:

.

Считая, что задана как функция угла , возьмем ее разложение в ряд Фурье:

,

где

;

;

.

Будем использовать формулы Эйлера:

;

.

Подставляя выражения для коэффициентов Фурье в решение и меняя порядок суммирования и интегрирования, получим:

Подставляя в это выражение фомулы Эйлера, получаем интегральную формулу, дающую решение задачи

3.3.2. Задача Дирихле для уравнения Лапласа в кольце

Найти функцию u, удовлетворяющую уравнению внутри кольца.

Необходимо поставить краевые условия на каждой из границ:

где – заданные функции; – полярный угол.

Для простоты вычислений возьмем и , тогда краевые условия примут вид

Из уравнения Лапласа в полярных координатах получаем систему обыкновенных дифференциальных уравнений

Необходимо определить знак .

В уравнении Лапласа в круге мы выяснили, что при

;

, .

И при получили

, .

Общее решение имеет вид

.

Удовлетворим краевым условиям. Необходимо выяснить, какие из коэффициентов являются лишними.

;

;

;

;

;

;

.

Итак, получили

Отсюда

– решение задачи.

3.3.3. Задача Дирихле для уравнения Лапласа в прямоугольнике

Для решения уравнения Лапласа в прямоугольнике необходимо рассмотреть вспомогательную задачу.

Решим эту задачу методом разделения переменных. Будем искать решение в виде

.

Уравнение примет вид

.

Отсюда получим два обыкновенных дифференциальных уравнения

Определим знак .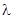

1. Пусть , например, .
Рассмотрим уравнение

.

Характеристическое уравнение имеет вид

Получаем – решение первого уравнения системы.

Рассмотрим уравнение

.

Характеристическое уравнение имеет вид

– решение второго уравнения системы.

Таким образом,

.

Удовлетворим краевым условиям:

;

.

, так как мы ищем ненулевые решения уравнения, тогда , отсюда .

.

Учитывая, что имеем:

.

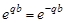, следовательно, .Это возможно только при , но тогда мы получим решение уравнения, равное постоянной, а это не удовлетворяет краевым условиям задачи.

2. Пусть , например, . Тогда решения системы уравнений имеют соответственно вид

;

.

Таким образом,

.

Удовлетворим краевым условиям:

.

, следовательно, .

.

Помня, что , имеем:

.

Так как при получим нулевое решение, то

.

Отсюда

.

Итак, получили решение

.

Подставим начальные условия:

.

Отсюда

;

.

Отсюда

.

Для нахождения коэффициентов и необходимо решить систему уравнений:

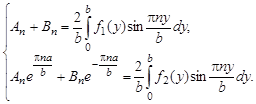
Подставив полученные коэффициенты, получим решение задачи.

Рассмотрим ненулевые краевые условия для уравнения Лапласа в прямоугольнике:

Решение задачи будем искать в виде суммы двух функций . Иными словами необходимо решить две системы уравнений:

и

Первая система уже решена. Для того чтобы найти решение второй системы, необходимо просто заменить соответствующие буквы и цифры в решении для ,т.е. .

 

Рекомендуемая литература

1. Блинова И.В., Попов И.Ю. Простейшие уравнения математической физики: учеб. пособие. – СПб., СПбГУ ИТМО, 2009.

2. Вержбицкий В.М. Основы численных методов. – М.: Высшая школа, 2002.

3. Каханер Д., Моулер К., Нэш С. Численные методы и программное обеспечение. – М.: Мир, 2001.

4. Мэтьюз Дж. Г., Финк Куртис Д. Численные методы. Использование MATLAB. – Москва– Санкт-Петербург – Киев, Вильямс, 2001.

5. Семченок М.С., Семченок Н.М. Система MATLAB: учеб. пособие. Ч. 1. – СПб., СПбГУКиТ, 2005.

6. Смирнов М.М. Дифференциальные уравнения в частных производных второго порядка. – М.: Наука, 1984.

7. Соболев С.Л. Уравнения математической физики. – М.: Наука, 1992.

8. Тихонов А.Н., Самарский А.А. Уравнения математической физики. – М.: МГУ, 2004.

Индивидуальные задания

1. Найти решение уравнения колебания полуограниченной струны ( ): , удовлетворяющее начальным и граничным условиям. Изобразить профиль струны для моментов времени

Номер вари- анта	а	l	Гранич- ные условия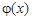

Продолжение

Номер вари- анта	а	l	Гранич- ные условия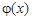

Окончание

Номер вари- анта	а	l	Гранич- ные условия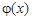

где

2. Найти решение уравнения теплопроводности в ограниченном стержне , удовлетворяющее начальному и следующим граничным условиям:

Номер варианта	а	l	Граничные условия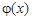

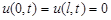
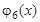
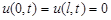
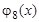
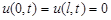
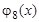
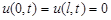
Найти решение уравнения колебания ограниченной струны , удовлетворяющее начальному и следующим граничным условиям:

Номер варианта	а	l	Граничные условия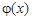

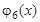
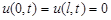
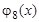
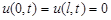
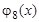
где

, ,

, ,

,

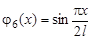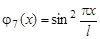Приложения

Практикум в среде MATLAB

Лабораторная работа № 1